平行线性质定理和判定定理的综合应用
文档属性
| 名称 | 平行线性质定理和判定定理的综合应用 |  | |
| 格式 | rar | ||
| 文件大小 | 54.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-20 13:59:00 | ||
图片预览




文档简介
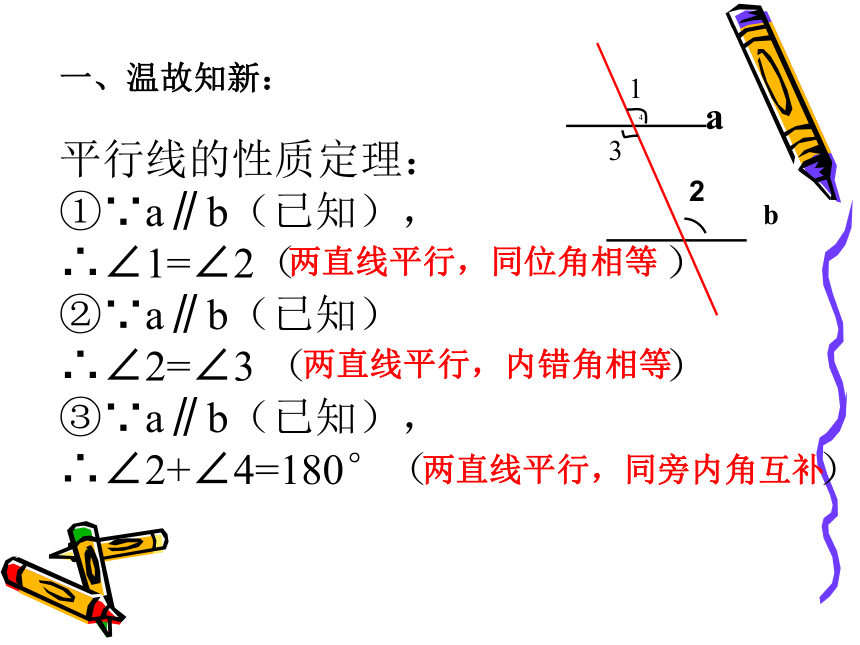
课件20张PPT。平行线性质定理和判定定理的综合应用平行线的性质定理:
①∵a∥b(已知),
∴∠1=∠2( )
②∵a∥b(已知)
∴∠2=∠3 ( )
③∵a∥b(已知),
∴∠2+∠4=180°( ) 两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补
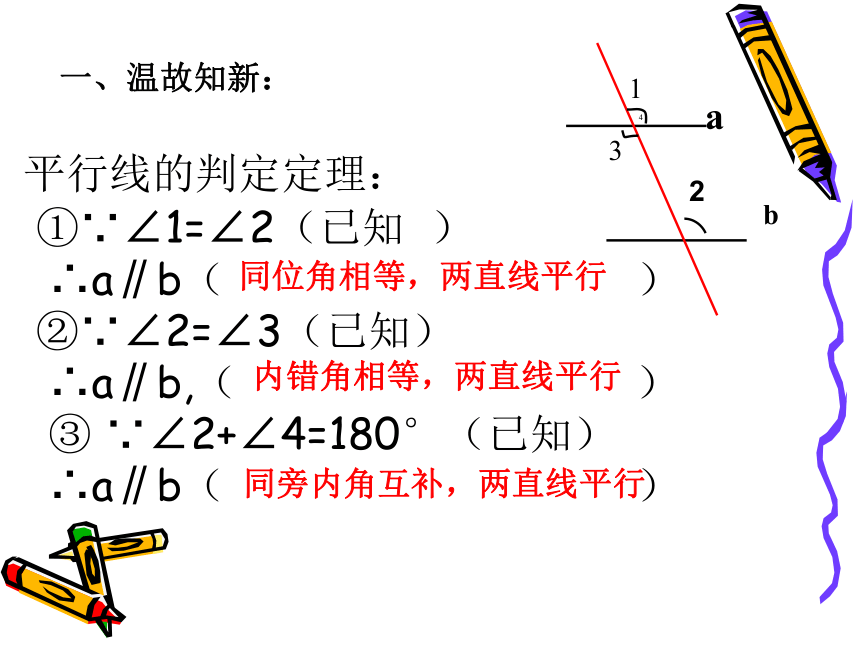
一、温故知新:平行线的判定定理:
①∵∠1=∠2(已知 )
∴a∥b( )
②∵∠2=∠3(已知)
∴a∥b,( )
③ ∵∠2+∠4=180°(已知)
∴a∥b( ) 同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行
一、温故知新:
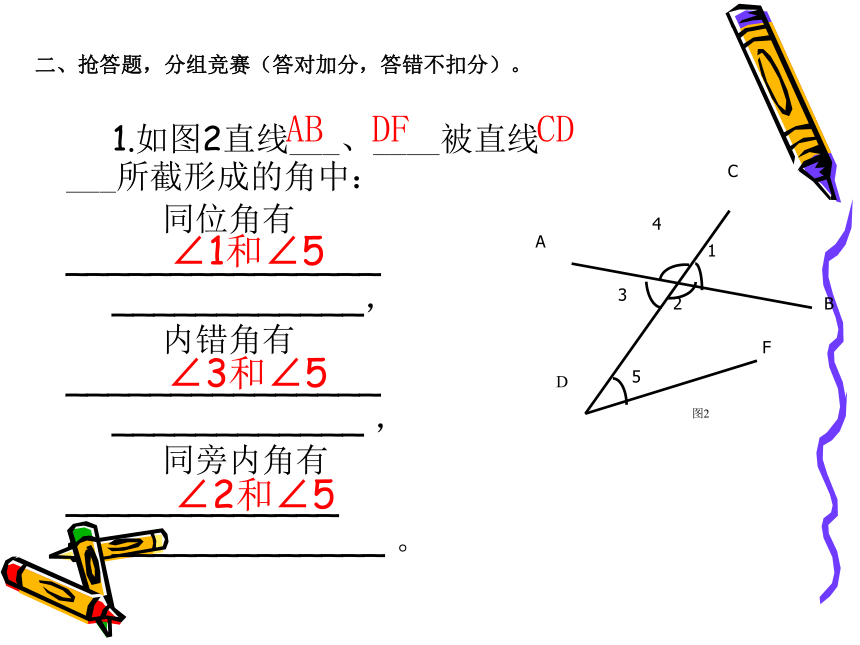
1.如图2直线___、____被直线___所截形成的角中:
同位角有_______________
____________,
内错角有_______________
____________ ,
同旁内角有_____________
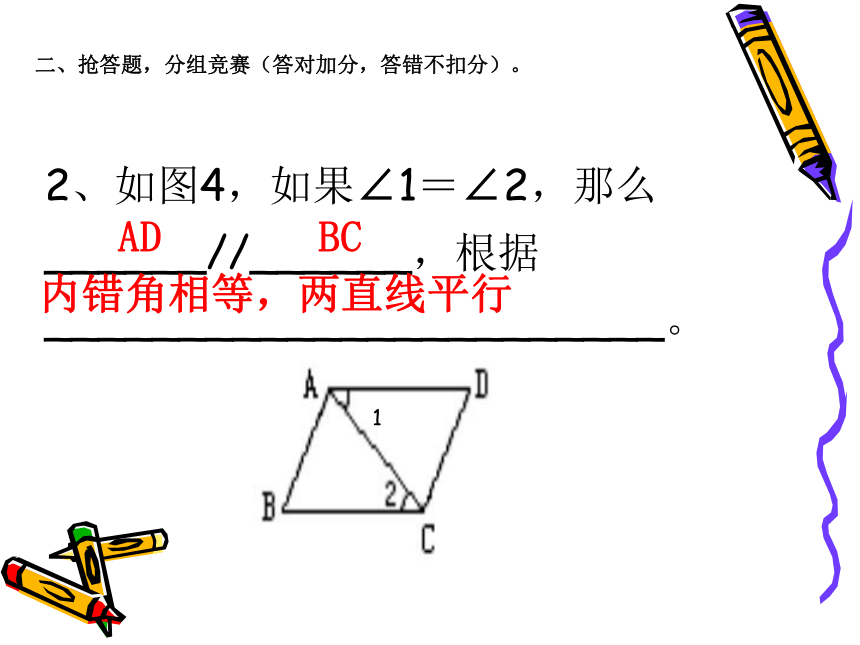
_____________ 。二、抢答题,分组竞赛(答对加分,答错不扣分)。∠1和∠5∠3和∠5∠2和∠5二、抢答题,分组竞赛(答对加分,答错不扣分)。2、如图4,如果∠1=∠2,那么
______//______,根据
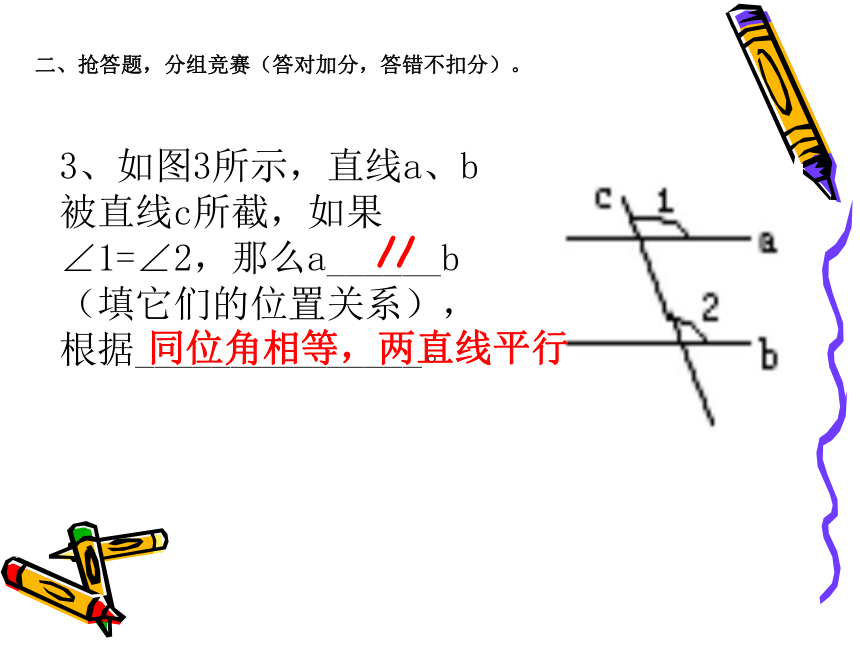
_______________________。内错角相等,两直线平行3、如图3所示,直线a、b被直线c所截,如果∠1=∠2,那么a______b(填它们的位置关系),根据_______________。二、抢答题,分组竞赛(答对加分,答错不扣分)。//同位角相等,两直线平行二、抢答题,分组竞赛(答对加分,答错不扣分)。4、如图5,一个弯形管道ABCD的拐角∠ABC=100°,∠BCD=80°,这时管道AB平行CD,它的根据是_______________________。 图5同旁内角互补,两直线平行二、抢答题,分组竞赛(答对加分,答错不扣分)。 5、已知三条直线a、b、c,如果a∥c, b∥c,那么a___b,这是因为______________________________________________;//如果两条直线都与第三条直线平行,
那么着两条直线也互相平行(三)解答题。 6、如图,木工师傅用角尺画出长方形工件边缘的两条垂线,这两条垂线是否平行( )。口述理由。(3分)
图12是理由:
同一平面内,垂直于同一条直线的两条直线互相平行。(二)选择题(每题1分)7、如图7:当AC//BD时,可以判断∠A等于哪个角。( )
A.∠D?? ? B.∠C??? C.∠B?? ? D.∠AOC图7c 8、如图8,已知∠1=∠2 ,且∠C=70° ,则∠ADC=( )
A、70° B、20°
C、110° D、无法确定C(二)选择题(每题1分)(二)选择题(每题1分) 9、如图9:当∠A=∠CBE时,可以判断哪两条直线平行。( )
A、AB//DC??? ? B、AD//BC???
C、AD//AE ???? D、BC//DC图9B(二)选择题(每题1分) 10、如图11:
当( )时,AB∥CD。
A、∠1=∠2 B、∠3=∠4??
C、∠B=∠D? D、∠3=∠2 图11B(二)选择题(每题1分)11、两条直线被第三条直线所截,有一对同位角相等,则下列结论:
(1)4对同位角都分别相等;
(2)2对内错角相等;
(3)2对同旁内角互补。
正确的是( )? A、1个 B、2个???
C、3个 ? D、0个C 12、如图13:已知:∠1=60°,∠2=60°,AB//CD:
求证:①∠2=∠3,
②CD//EF。(5分)(三)解答题(2分)。(三)解答题12题解题过程。
证明:
① ∵∠1=60°,∠2=60°( ) ??? ∴∠1=∠2 ??? ∵∠1=∠3( ) ??? ∴∠2=∠3( ) 已知对顶角相等等量代换(三)解答题(2分)。② ∵ ∠2=∠3(已证) ??∴AB//EF( ) ??∵AB//CD(已知) ??∴CD//EF(
) 同位角相等,两直线平行 平行于同一条直线的两直线
互相平行 三、综合应用题 15、 如右图: 已知,AB与CD相交于点E,且∠1+∠D=180°;求证:AB//DF。
证明:
∵AEB为一直线(已知) ?
∴∠1+∠2=180°(邻补角定义) ∵∠1+∠D=180°(已知) ? ∴∠2=∠D(同角的补角相等) ? ∴AB//DF(同位角相等,两直线平行)三、综合应用题 16.已知:如右图,BE平分∠ABC,∠1=∠2,求证:①∠2=∠3;
②∠4=∠C
证明:
∵ BE平分∠ABC(已知) ∴ ∠1=∠3(角平分线定义) 又∵ ∠1=∠2(已知) ∴ ∠2=∠3(等量代换)
∴ DE∥BC(内错角相等,两直线平行)
∴ ∠4=∠C(两直线平行,同位角相等)祝同学们学习愉快谢谢各位老师的莅临指导
①∵a∥b(已知),
∴∠1=∠2( )
②∵a∥b(已知)
∴∠2=∠3 ( )
③∵a∥b(已知),
∴∠2+∠4=180°( ) 两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补
一、温故知新:平行线的判定定理:
①∵∠1=∠2(已知 )
∴a∥b( )
②∵∠2=∠3(已知)
∴a∥b,( )
③ ∵∠2+∠4=180°(已知)
∴a∥b( ) 同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行
一、温故知新:
1.如图2直线___、____被直线___所截形成的角中:
同位角有_______________
____________,
内错角有_______________
____________ ,
同旁内角有_____________
_____________ 。二、抢答题,分组竞赛(答对加分,答错不扣分)。∠1和∠5∠3和∠5∠2和∠5二、抢答题,分组竞赛(答对加分,答错不扣分)。2、如图4,如果∠1=∠2,那么
______//______,根据
_______________________。内错角相等,两直线平行3、如图3所示,直线a、b被直线c所截,如果∠1=∠2,那么a______b(填它们的位置关系),根据_______________。二、抢答题,分组竞赛(答对加分,答错不扣分)。//同位角相等,两直线平行二、抢答题,分组竞赛(答对加分,答错不扣分)。4、如图5,一个弯形管道ABCD的拐角∠ABC=100°,∠BCD=80°,这时管道AB平行CD,它的根据是_______________________。 图5同旁内角互补,两直线平行二、抢答题,分组竞赛(答对加分,答错不扣分)。 5、已知三条直线a、b、c,如果a∥c, b∥c,那么a___b,这是因为______________________________________________;//如果两条直线都与第三条直线平行,
那么着两条直线也互相平行(三)解答题。 6、如图,木工师傅用角尺画出长方形工件边缘的两条垂线,这两条垂线是否平行( )。口述理由。(3分)
图12是理由:
同一平面内,垂直于同一条直线的两条直线互相平行。(二)选择题(每题1分)7、如图7:当AC//BD时,可以判断∠A等于哪个角。( )
A.∠D?? ? B.∠C??? C.∠B?? ? D.∠AOC图7c 8、如图8,已知∠1=∠2 ,且∠C=70° ,则∠ADC=( )
A、70° B、20°
C、110° D、无法确定C(二)选择题(每题1分)(二)选择题(每题1分) 9、如图9:当∠A=∠CBE时,可以判断哪两条直线平行。( )
A、AB//DC??? ? B、AD//BC???
C、AD//AE ???? D、BC//DC图9B(二)选择题(每题1分) 10、如图11:
当( )时,AB∥CD。
A、∠1=∠2 B、∠3=∠4??
C、∠B=∠D? D、∠3=∠2 图11B(二)选择题(每题1分)11、两条直线被第三条直线所截,有一对同位角相等,则下列结论:
(1)4对同位角都分别相等;
(2)2对内错角相等;
(3)2对同旁内角互补。
正确的是( )? A、1个 B、2个???
C、3个 ? D、0个C 12、如图13:已知:∠1=60°,∠2=60°,AB//CD:
求证:①∠2=∠3,
②CD//EF。(5分)(三)解答题(2分)。(三)解答题12题解题过程。
证明:
① ∵∠1=60°,∠2=60°( ) ??? ∴∠1=∠2 ??? ∵∠1=∠3( ) ??? ∴∠2=∠3( ) 已知对顶角相等等量代换(三)解答题(2分)。② ∵ ∠2=∠3(已证) ??∴AB//EF( ) ??∵AB//CD(已知) ??∴CD//EF(
) 同位角相等,两直线平行 平行于同一条直线的两直线
互相平行 三、综合应用题 15、 如右图: 已知,AB与CD相交于点E,且∠1+∠D=180°;求证:AB//DF。
证明:
∵AEB为一直线(已知) ?
∴∠1+∠2=180°(邻补角定义) ∵∠1+∠D=180°(已知) ? ∴∠2=∠D(同角的补角相等) ? ∴AB//DF(同位角相等,两直线平行)三、综合应用题 16.已知:如右图,BE平分∠ABC,∠1=∠2,求证:①∠2=∠3;
②∠4=∠C
证明:
∵ BE平分∠ABC(已知) ∴ ∠1=∠3(角平分线定义) 又∵ ∠1=∠2(已知) ∴ ∠2=∠3(等量代换)
∴ DE∥BC(内错角相等,两直线平行)
∴ ∠4=∠C(两直线平行,同位角相等)祝同学们学习愉快谢谢各位老师的莅临指导
