4.4 一次函数的应用（1）课件

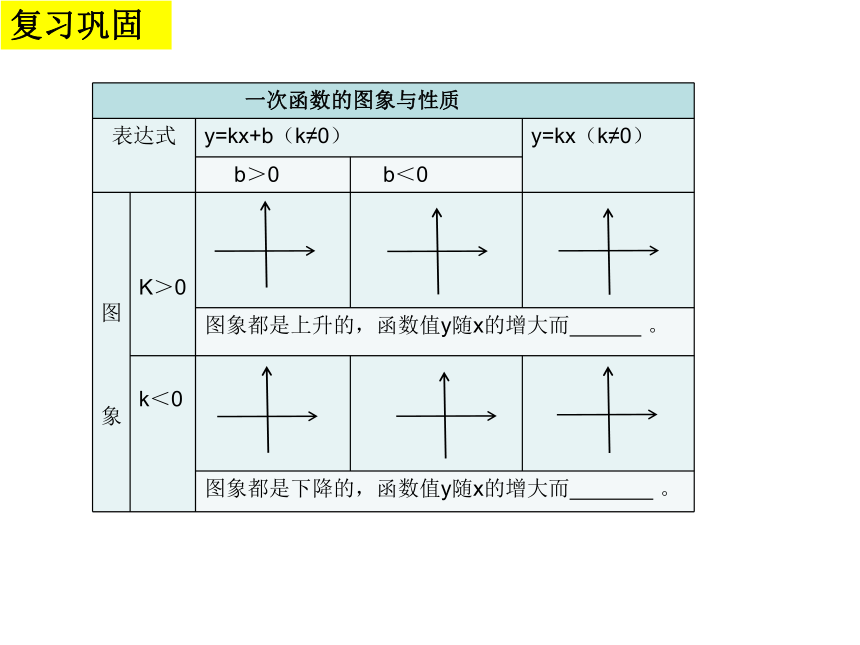
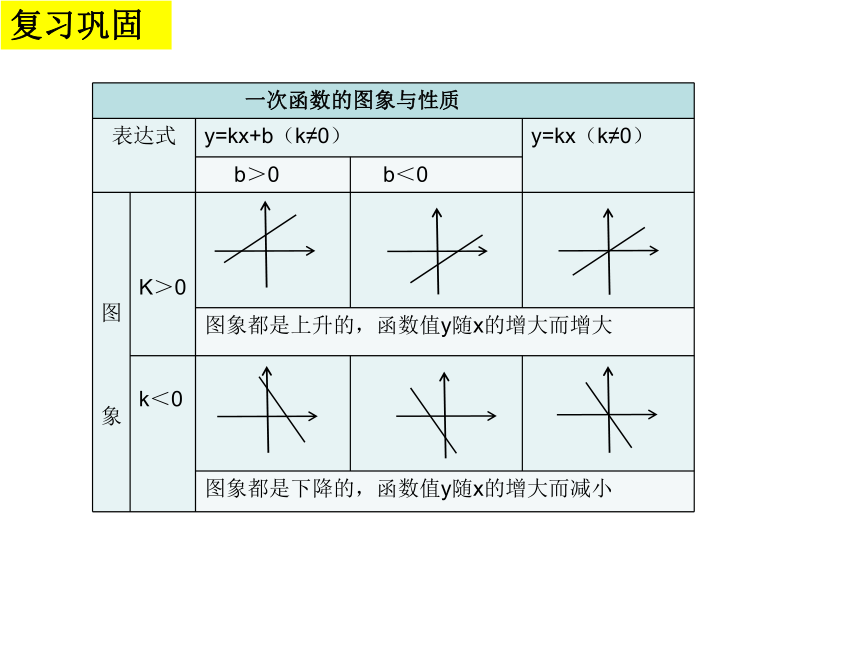
课件17张PPT。4.4 一次函数的应用 第1课时复习巩固复习巩固复习巩固1、一次函数y=2x+3中，当x=3时，y= 。当y=5时，x= 。
2.根据点（3,4）得x= ,y= 。
3、在一次函数y=kx+b的图象上有一点（4,5），

把（4,5）代入y=kx+b得 。要求：1.同桌组员说组长听，不同意见要交流 ，

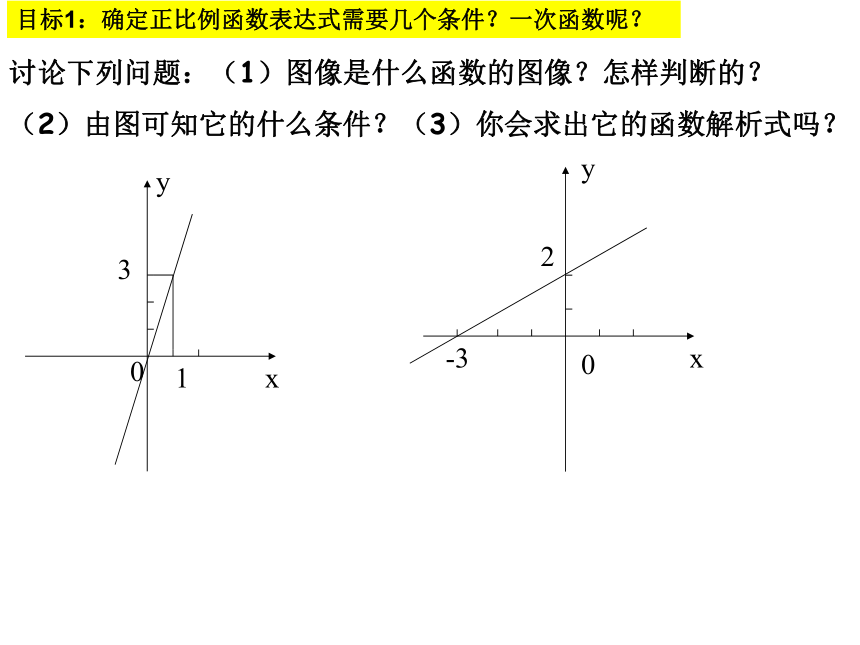
2.同桌小组有争议寻求组内帮助。1.确定正比例函数表达式需要几个条件？一次函数呢？
2.会用待定系数法解决简单的实际问题.3.能根据函数的图象确定一次函数的表达式.讨论下列问题：（1）图像是什么函数的图像？怎样判断的？
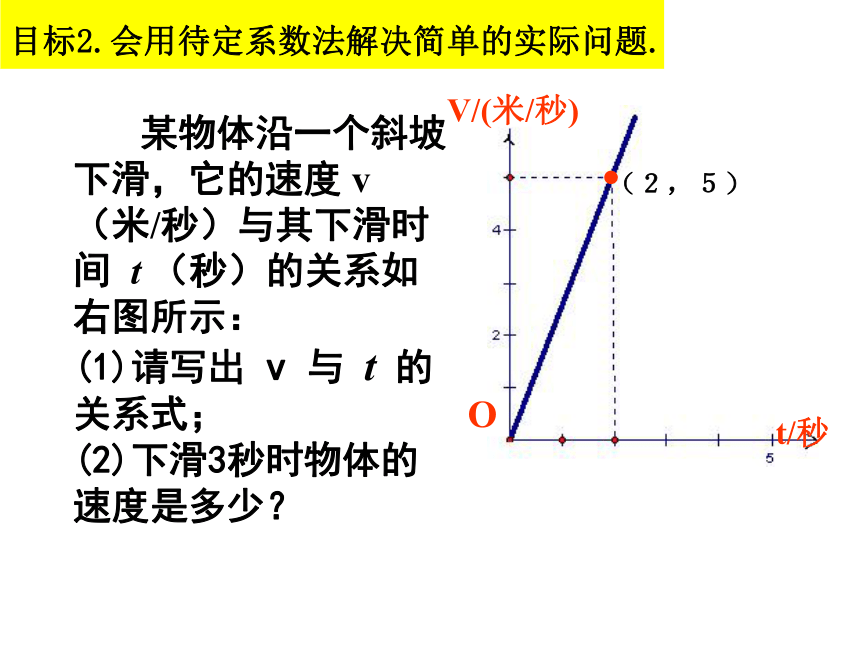
（2）由图可知它的什么条件？（3）你会求出它的函数解析式吗？目标1：确定正比例函数表达式需要几个条件？一次函数呢？目标2.会用待定系数法解决简单的实际问题.V/(米/秒)t/秒O 某物体沿一个斜坡下滑，它的速度 v （米/秒）与其下滑时间 t （秒）的关系如右图所示： (1)请写出 v 与 t 的关系式； (2)下滑3秒时物体的速度是多少？（２，５）V/(米/秒)t/秒O 某物体沿一个斜坡下滑，它的速度 v （米/秒）与其下滑时间 t （秒）的关系如右图所示： (1)请写出 v 与 t 的关系式； (2)下滑3秒时物体的速度是多少？(V=2.5t)(V=７.５米／秒)（２，５）解：设Ｖ＝kt;
∵(2,5)在图象上
∴５＝2k
k=2.5
∴V=2.5t目标2.会用待定系数法解决简单的实际问题.总结：确定 一次函数表达式所需要的步骤是什么？温馨提示：1：结合上面的解题步骤，都经历了哪些过程？

2：同桌两人交流，先组员说，后组长补充。
3：说完即坐，不到之处，其他组继续补充。解：设Ｖ＝kt;
∵(2,5)在图象上
∴５＝2k
k=2.5
∴V=2.5t思考：确定 一次函数表达式所需要的步骤是什么？1、设——设函数表达式y=kx+b
2、代——将点的坐标代入y=kx+b中，
列出关于k、b的方程3、求——解方程，求k、b4、写——把求出的k、b值
代回到表达式中即可例.在弹性限度内，弹簧的长度y（cm）是所挂物体质量
x（kg）的一次函数.一根弹簧不挂物体时长14.5 cm ；当所挂物体的质量为3 kg时，弹簧长16 cm.请写出 y 与x之间的关系式，并求当所挂物体的质量为4 kg时弹簧的长度.目标2.会用待定系数法解决简单的实际问题.解：设y=kx+b(k≠0)
把（0,14.5）和（3,16）代入，得：
14.5=b,
16=3k+b,
解得：b=14.5 ; k=0.5.所以在弹性限度内，
当x=4时，y＝０.５×４＋14.5=16.5（厘米）.
即物体的质量为４千克时，弹簧长度为１６.５厘米.目标2.会用待定系数法解决简单的实际问题.问题解决：从地面竖直向上抛射一个物体，在落地之前，物体向上的速度v(m/s)是运动时间的t(s)的一次函数，经测量，该物体的初始速度为(t=0时物体的速度）为25m/s，2s后物体的速度为5m/s，
（1）写出v,t之间的关系式；
（2）经过多长时间后，物体将达到最高点？（此时物体的速度为0）1、若一次函数的图象如图所示，求一次函数解析式。
2.如图，求直线a与两坐标轴围成的三角形的面积。
第1题第2题a数形结合：目标3.根据图象确定一次函数表达式1、如图:（1）求AB的解析式
（2）求三角形AOC的面积拓展提升Dyx1、在弹性范围内弹簧的长度y( cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )
A.8cm B.9cm
C.10.5cm D.11cm学以致用小结：１. 设——设一次函数表达式；
２. 列——根据已知条件列出有关方程；
３. 解——解方程（组）；
４.代—— 把求出的k，b代回表达式即可.
2．本节课用到的主要的数学思想方法：
数形结合、方程的思想．