4.3 相似多边形 课件

课件19张PPT。
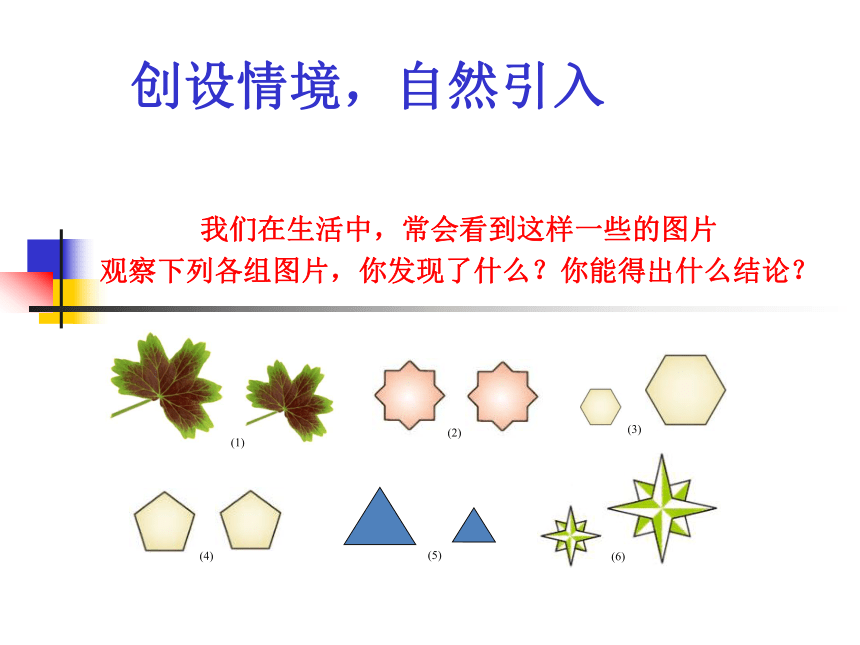
4.3 相似多边形创设情境，自然引入我们在生活中，常会看到这样一些的图片
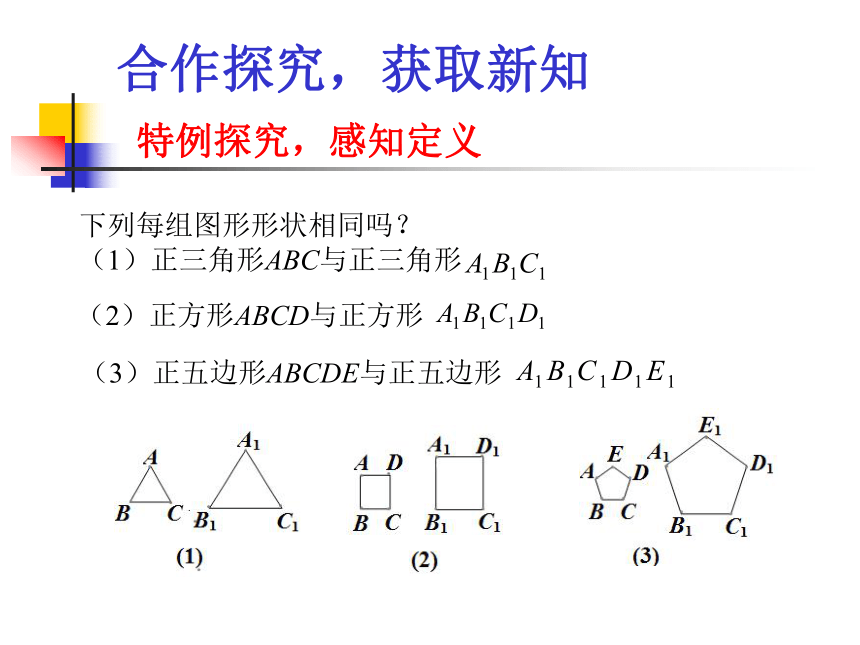
观察下列各组图片，你发现了什么？你能得出什么结论？合作探究，获取新知 特例探究，感知定义下列每组图形形状相同吗？
（1）正三角形ABC与正三角形（2）正方形ABCD与正方形 （3）正五边形ABCDE与正五边形

（1）在每组图形中，是否有对应相等的内角？设法验证你的猜测．
（2）在每组图形中，夹相等内角的两边是
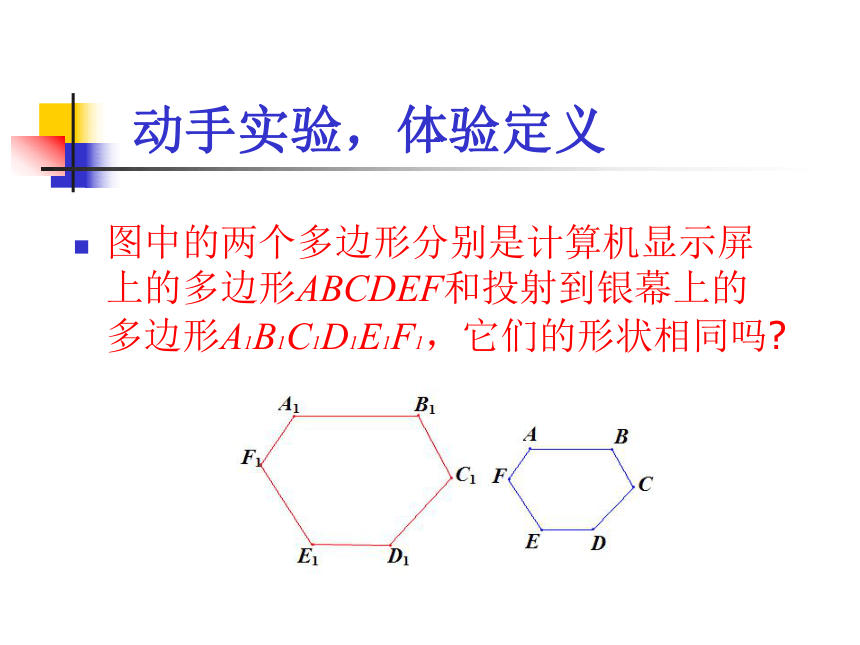
否成比例？想一想：动手实验，体验定义图中的两个多边形分别是计算机显示屏上的多边形ABCDEF和投射到银幕上的多边形A1B1C1D1E1F1，它们的形状相同吗? （1）在这两个多边形中，是否有对应相等 内角？设法验证你的猜测．
（2）在这两个多边形中，夹相等内角的两边是否成比例？ 想一想：强调说明：在上图中，六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的多边形，其中∠A与∠A1，∠B与∠B1，∠C与∠C1，∠D与∠D1，∠E与∠E1，∠F与∠F1，分别相等，称为对应角；
AB与A1B1，BC与B1C1，CD与C1D1，DE与D1E1，EF与E1F1，FA与F1 A1的比都相等，称为对应边．
归纳总结，形成概念 回忆一下我们刚才探究过的每一组多边形，你能发现它们的共同特点吗？相似多边形的概念：
各角分别相等、各边成比例的两个多边形叫做相似多边形（Similar polygons）.例如，在上图中六边形ABCDEF与六边形A1B1C1D1E1F1相似，记作六边形ABCDEF∽六边形A1B1C1D1E1F1， “∽”读作“相似于”．
相似比的概念：
相似多边形对应边的比叫做相似比（Similarity ratio）.
强调说明：(1)在记两个多边形相似时，要把对应顶点字母写在对应的位置上.
(2)相似多边形的定义既是最基本、最重要的判定方法，也是最本质、最重要的性质.
(3)相似比有顺序性.例如，五边形ABCDE∽五边形A1B1C1D1E1，对应边的比为
因此五边形ABCDE与五边形A1B1C1D1E1的相似比
五边形 A1B1C1D1E1与五边形ABCDE的相似比

(4)相似比为1的两个图形是全等形. 因此全等形是相似图形特殊情况.
反例分析，深化理解 (1)观察下面两组图形，图（1）中的两个图形相似吗？
图（2）中的两个图形呢？为什么？你从中得到什么
启发？与同桌交流. (2)如果两个多边形不相似，那么它们的各角可能对应相等吗？它们的各边可能对应成比例吗？ 典例探究，深化新知 提出问题：一块长3m、宽1.5m的矩形黑板如图所示，镶在其外围的木质边框7.5cm.边框的内外边缘所成的矩形相似吗？为什么？解:∵四边形ABCD与矩形A1B1C1D1均为矩形
∴∠A =∠A1，∠B=∠B1，∠C=∠C1，∠D=∠D1，
由题意得AB=315，BC=165
∴
∴ ≠
∴矩形ABCD和矩形A1B1C1D1不相似.在上题中，如果镶的纵向边框宽7.5cm，那么当镶的横向边框宽为多少时，边框的内外边缘所成的矩形相似？. 想一想：解：设镶的横向边框宽为xcm.
由题意得.
解得x=30.
经检验符合题意.
答当镶的横向边框宽为30cm时，边框 的内外边缘所成的矩形相似.回顾反思，提炼升华 通过这节课的学习，你有哪些收获？有何感想？学会了哪些方法？先想一想，再分享给大家．
通过本节课的学习，同学们经历从特殊到一般探究过程，认识到全等图形是相似比于1的相似图形，相似图形是全等图形的进一步的推广，理解了相似多边形的概念既是性质又是判定，运用性质时对应顶点字母写在对应的位置上，同时知道相等角所对边是对应边，对应边所对角是对应角．体会了相似比是有顺序要求．达标检测，反馈提高 1．如果四边形ABCD∽ 四边形 相似，且∠A=68°,则∠ = ．
2．一个多边形的边长分别是2、3、4、5、6，另一个和它相似的多边形的最短边长为6，则这个多边形的最长边为 ．
3．下列说法中正确的是（ ）
A、所有的矩形都相似 B、所有的正方形都相似
C、所有的菱形都相似 D、所有的正多边形都相似挑战自我，相信你能行！ 68°18B4．如图所示的两个矩形相似吗？为什么？如果相似，相似比是多少？达标检测，反馈提高 加油，你是最棒的！4．相似，2:1；1:2．布置作业，课堂延伸 基础作业：课本 P88 习题4.4 第1题，第2题．
拓展作业：课本 P88 ,习题4.4 第3题，第4题．祝愿同学们：像雄鹰一样
飞的更高，
飞的更远！