幂的乘方与积的乘方

课件13张PPT。第一章 整 式幂的乘方与积的乘方回顾与思考am · an= am+n?幂的意义:an=am+n（m,n都是正整数）推导过程 乙正方体的边长是 2 cm, 则乙正方体的体积 V乙= cm3 V甲 是 V乙 的 倍8125即 53 倍 正方体的体积比与边长比的关系边长比的立方。 甲正方体的边长是乙正方体的 5 倍，则
甲正方体的体积 V甲= cm31000 乙球的半径为 3 cm, 则
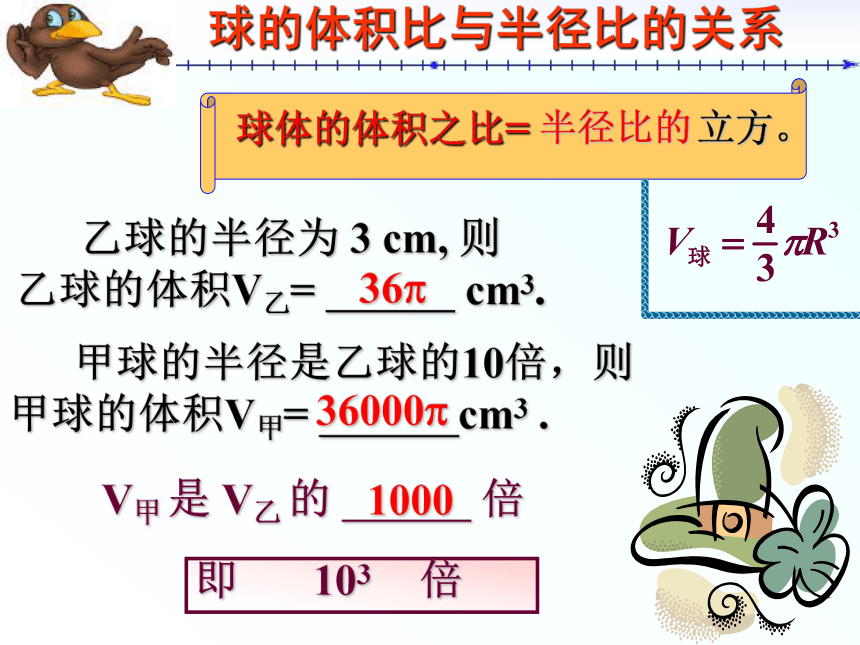
乙球的体积V乙= cm3.V甲 是 V乙 的 倍即 103 倍 球的体积比与半径比的关系半径比的立方。 甲球的半径是乙球的10倍，则
甲球的体积V甲= cm3 .100036?36000?体积扩大的倍数比半径扩大的倍数大得多.如果甲球的半径是乙球的n 倍，那么甲球体积是乙球体积的 倍。n3 103106(102)3=102×102×102=102+2+2=102×3=106太棒了(根据 ).(根据 ).同底数幂的乘法性质幂的意义(102)3=106，为什么？做一做 计算下列各式，并说明理由 .
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .解：(1) (62)4 (2) (a2)3(3) (am)2= 62·62· 62·62=62+2+2+2=68= a2·a2·a2=a2+2+2=a6=am·am=am+m(4) (am)n=am·am· … ·am=am+m+ … +m=amn（幂的意义）（同底数幂的乘法性质）（乘法的意义）amn证明nn(am)n=amn (m,n都是正整数)底数 ，指数 . 幂的乘方，幂 的 乘 方 法则不变相乘例题解析例题解析 【例1】计算：
(1) (102)3 ; (2) (b5)5 ; (3) (an)3;
(4) -(x2)m ; (5) (y2)3 · y ; (6) 2(a2)6 － (a3)4 . (6) 2(a2)6 – (a3)4=102×3=106 ;(1) (102)3解：(2) (b5)5= b5×5= b25 ;(3) (an)3= an×3=a3n ;(4) -(x2)m= -x2×m= -x2m ;(5) (y2)3 · y= y2×3 · y= y6 · y=2a2×6 - a3×4=2a12-a12=a12.= y7; 阅读 ? 体验 ?随堂练习 1、计算：
(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 . 2. 判断下面计算是否正确？如果有错误请改正：
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .本节课你的收获是什么？小结本节课你学到了什么?相乘不变联系拓广⑴ a12 ＝（a3）( ) ＝（a2）( )＝a3 a( )＝（ ）3 ＝（ ）4⑵ 32﹒9m ＝3( )⑶ y3n ＝3, y9n ＝ .
⑷ （a2）m+1 ＝ .
⑸ [（a-b）3 ]2＝（b-a ）( )
联系拓广(7)如果 2a＝3 ,2b＝6 ,2c＝12, 那么 a，b，c的关系是 .(6)若4﹒8m﹒16m ＝29 ， 则m＝ .