人教版四年级数学上《8.3赛马问题》-课件
文档属性
| 名称 | 人教版四年级数学上《8.3赛马问题》-课件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-08 09:47:11 | ||
图片预览





文档简介
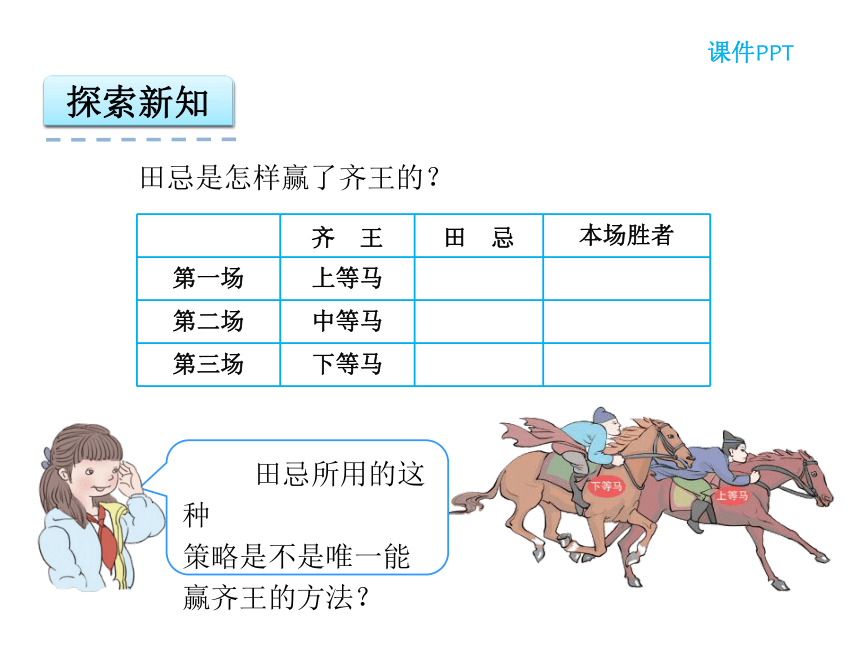
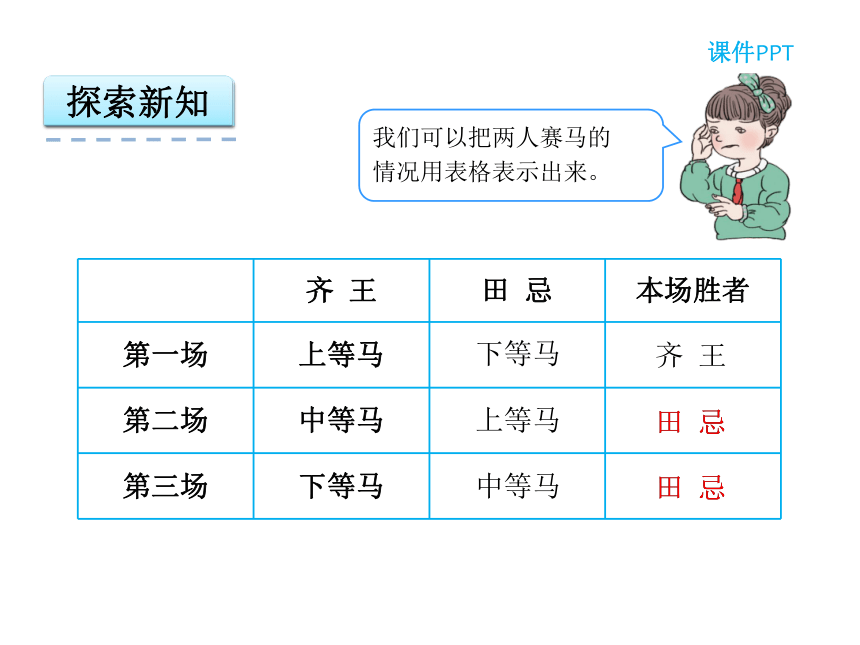
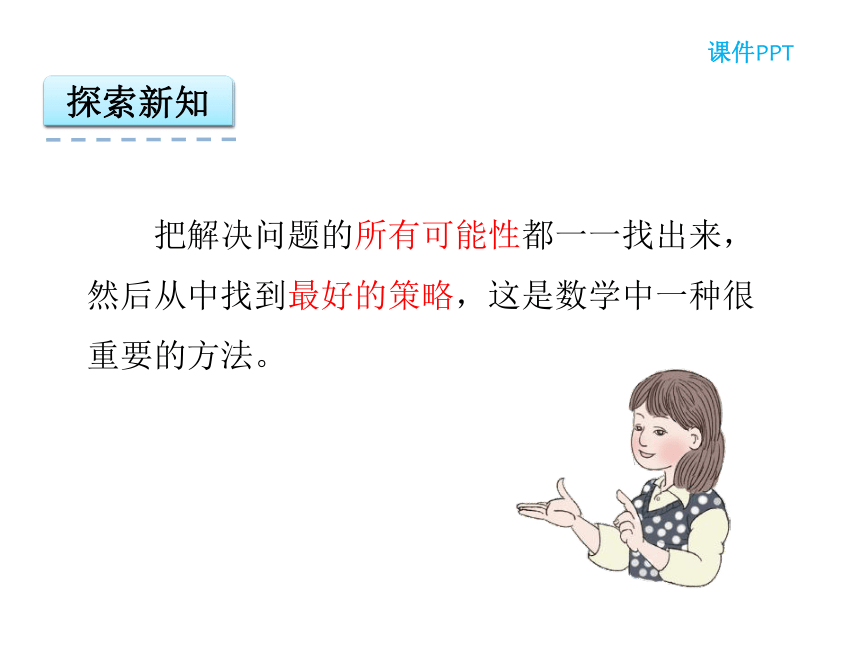
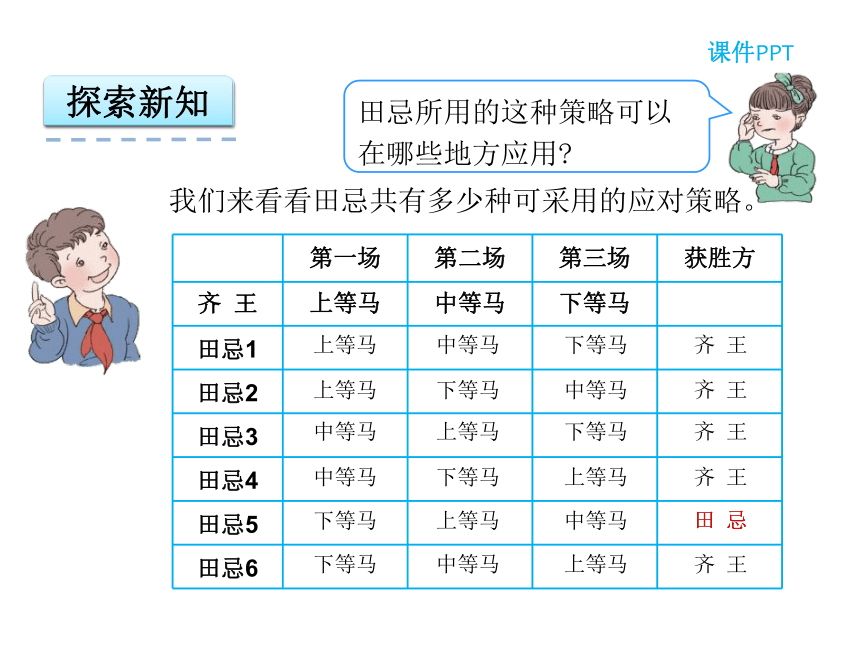
课件22张PPT。第8单元 数学广角——优化3 赛马问题学习目标3.提高应用意识,培养学习数学的兴趣。1. 通过赛马问题,初步体会统筹思想在解决实际问题中的应用。2.认识到解决同一个问题有不同的策略,能够找到解决问题的最优方案。同学们,你听过“田忌赛马”的故事吗?绿色圃中小学教育网http://www.lspjy.com情景导入课件PPT探索新知课件PPT田忌是怎样赢了齐王的?绿色圃中小学教育网http://www.lspjy.com绿色圃中小学教育网http://www.lspjy.com探索新知课件PPT田 忌田 忌田 忌田 忌下等马上等马中等马齐 王探索新知课件PPT 把解决问题的所有可能性都一一找出来,
然后从中找到最好的策略,这是数学中一种很
重要的方法。 探索新知课件PPT田 忌田 忌我们来看看田忌共有多少种可采用的应对策略。上等马中等马下等马齐 王上等马下等马中等马齐 王齐 王齐 王齐 王中等马上等马下等马中等马下等马上等马下等马下等马上等马上等马中等马中等马探索新知课件PPT典题精讲 欢欢和乐乐两人玩夺红旗的游戏。规则:两人轮流数数,每次至少数一个(如1),最多数三个(如1、2、3),后面的人要接着前面的往后数,谁数到21(得到红旗)谁就获胜。先数获胜还是后数获胜?获胜的策略是什么?典题精讲解题思路: 画图从最后的结果分析。 21为红旗,占到前面的17才能抢到红旗(给对方留下4个数,对方不能一下数到21,而对方只要数了一个,自己最终都能数到21)。同样的道理,要抢到17,就必须抢到前面的13、9、5、1这些关键数,可以看到,先数者有一定获胜的策略。 先数有必胜的策略。先数1,然后依次占到5、9、13、17这些关键数,就能抢到21。典题精讲正确解答:错误解答易错提醒刘乐军——郑小鹏
孙翔宇——周大力李向阳——王小平 班级对抗赛每人打一场,最后以三场两胜制决定班级胜负。如果你是四(1)班的班长,你如何安排才能使本班获胜的可能性大呢?错解分析:易错提醒 错误解答错在没有运用“赛马问题”的技巧,先用李向阳—郑小鹏(四(1)输的可能大),再用刘乐军—周大力(四(1)赢的可能大),最后用孙翔宇—王小平(四(1)赢的可能大)。易错提醒正确解答错误解答刘乐军——郑小鹏
孙翔宇——周大力
李向阳——王小平李向阳——郑小鹏
刘乐军——周大力
孙翔宇——王小平 我们学校下个星期举行跳绳比赛,我们班和四(2)班对阵。比赛规则是每班选派3名选手,三局两胜。
四(3)班代表队 四(2)班代表队
李 明 105个/分 齐 航 110个/分
徐 青 90个/分 王 娜 95个/分
贾梦婷 60个/分 李 萌 75个/分 请同学们帮助我排兵布阵,如何才能战胜四(2)班?学以致用课件PPT 两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁就获胜。想一想:如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报? 想:因为每次只能报1和2,那么如果一方报1,另一方就可以报2,一方报2,另一方就可以报1。这样总能保证每个回合连续报数之和是3。因为谁最后报数之和是10谁获胜,所以一定要设法最后一个回合之前所有报数之和是7,这样对方无论怎样接着报数,你都可以保证最后报数之和是10。学以致用课件PPT 两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁就获胜。想一想:如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报?10÷3=3……1 想获胜的一方应先报1。接下来对如果对方报2,你就报1;对方报1,你就报2;保证每个回合两人报数之和为3,这样你就能确保胜利。1+2=3学以致用课件PPT 有2008个棋子,两人轮流取。每次最多取4个,最少取1个,不能不取。谁取到最后一粒谁就获胜,你有什么方法能确保获胜吗?1+4=52008÷5=401……3 想获胜方应先取3个。接下来对方如果取1个,你就取4个;对方取2个,你就取3个;对方取3个,你就取2个……,保证每个回合两人取的棋子和为5。这样你就能确保胜利。学以致用课件PPT 两人玩扑克牌比大小的
游戏,每人每次出一张牌,
各出3次,赢两次者胜。 学以致用课件PPT小 红小 红小 红小 红937856对 方绿色圃中小学教育网http://www.lspjy.com学以致用课件PPT课堂小结 1.解决同一个问题可以有不同的策略,但要学会寻找解决问题的最优方案。 肯于动脑,才能寻找到最优方案。 2.在与对方进行比赛时,要详细地分析自己与对方的情况,反复研究各种对策,在所有可能采取的策略中,选择一个利多弊少的最优策略,从而使劣势变为优势,最终取得胜利。谢谢
然后从中找到最好的策略,这是数学中一种很
重要的方法。 探索新知课件PPT田 忌田 忌我们来看看田忌共有多少种可采用的应对策略。上等马中等马下等马齐 王上等马下等马中等马齐 王齐 王齐 王齐 王中等马上等马下等马中等马下等马上等马下等马下等马上等马上等马中等马中等马探索新知课件PPT典题精讲 欢欢和乐乐两人玩夺红旗的游戏。规则:两人轮流数数,每次至少数一个(如1),最多数三个(如1、2、3),后面的人要接着前面的往后数,谁数到21(得到红旗)谁就获胜。先数获胜还是后数获胜?获胜的策略是什么?典题精讲解题思路: 画图从最后的结果分析。 21为红旗,占到前面的17才能抢到红旗(给对方留下4个数,对方不能一下数到21,而对方只要数了一个,自己最终都能数到21)。同样的道理,要抢到17,就必须抢到前面的13、9、5、1这些关键数,可以看到,先数者有一定获胜的策略。 先数有必胜的策略。先数1,然后依次占到5、9、13、17这些关键数,就能抢到21。典题精讲正确解答:错误解答易错提醒刘乐军——郑小鹏
孙翔宇——周大力李向阳——王小平 班级对抗赛每人打一场,最后以三场两胜制决定班级胜负。如果你是四(1)班的班长,你如何安排才能使本班获胜的可能性大呢?错解分析:易错提醒 错误解答错在没有运用“赛马问题”的技巧,先用李向阳—郑小鹏(四(1)输的可能大),再用刘乐军—周大力(四(1)赢的可能大),最后用孙翔宇—王小平(四(1)赢的可能大)。易错提醒正确解答错误解答刘乐军——郑小鹏
孙翔宇——周大力
李向阳——王小平李向阳——郑小鹏
刘乐军——周大力
孙翔宇——王小平 我们学校下个星期举行跳绳比赛,我们班和四(2)班对阵。比赛规则是每班选派3名选手,三局两胜。
四(3)班代表队 四(2)班代表队
李 明 105个/分 齐 航 110个/分
徐 青 90个/分 王 娜 95个/分
贾梦婷 60个/分 李 萌 75个/分 请同学们帮助我排兵布阵,如何才能战胜四(2)班?学以致用课件PPT 两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁就获胜。想一想:如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报? 想:因为每次只能报1和2,那么如果一方报1,另一方就可以报2,一方报2,另一方就可以报1。这样总能保证每个回合连续报数之和是3。因为谁最后报数之和是10谁获胜,所以一定要设法最后一个回合之前所有报数之和是7,这样对方无论怎样接着报数,你都可以保证最后报数之和是10。学以致用课件PPT 两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁就获胜。想一想:如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报?10÷3=3……1 想获胜的一方应先报1。接下来对如果对方报2,你就报1;对方报1,你就报2;保证每个回合两人报数之和为3,这样你就能确保胜利。1+2=3学以致用课件PPT 有2008个棋子,两人轮流取。每次最多取4个,最少取1个,不能不取。谁取到最后一粒谁就获胜,你有什么方法能确保获胜吗?1+4=52008÷5=401……3 想获胜方应先取3个。接下来对方如果取1个,你就取4个;对方取2个,你就取3个;对方取3个,你就取2个……,保证每个回合两人取的棋子和为5。这样你就能确保胜利。学以致用课件PPT 两人玩扑克牌比大小的
游戏,每人每次出一张牌,
各出3次,赢两次者胜。 学以致用课件PPT小 红小 红小 红小 红937856对 方绿色圃中小学教育网http://www.lspjy.com学以致用课件PPT课堂小结 1.解决同一个问题可以有不同的策略,但要学会寻找解决问题的最优方案。 肯于动脑,才能寻找到最优方案。 2.在与对方进行比赛时,要详细地分析自己与对方的情况,反复研究各种对策,在所有可能采取的策略中,选择一个利多弊少的最优策略,从而使劣势变为优势,最终取得胜利。谢谢
