2017年八年级数学北师大版课件 3-2 图形的旋转 (共19张PPT)
文档属性
| 名称 | 2017年八年级数学北师大版课件 3-2 图形的旋转 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-08 15:45:12 | ||
图片预览





文档简介
课件19张PPT。3.2 图形的旋转(一)第三章 图形的平移与旋转柴门中学 王海梅●理清学习目标1.掌握旋转的有关概念,理解旋转变换是图形的一种基本变换.
2.理解旋转的性质. 以上情景中的转动现象,有什么共同特征? 钟表的指针在转动过程中,其形状、
大小、位置是否发生改变?
飞机的螺旋桨、电风扇的叶轮的转动呢?观察思考︵
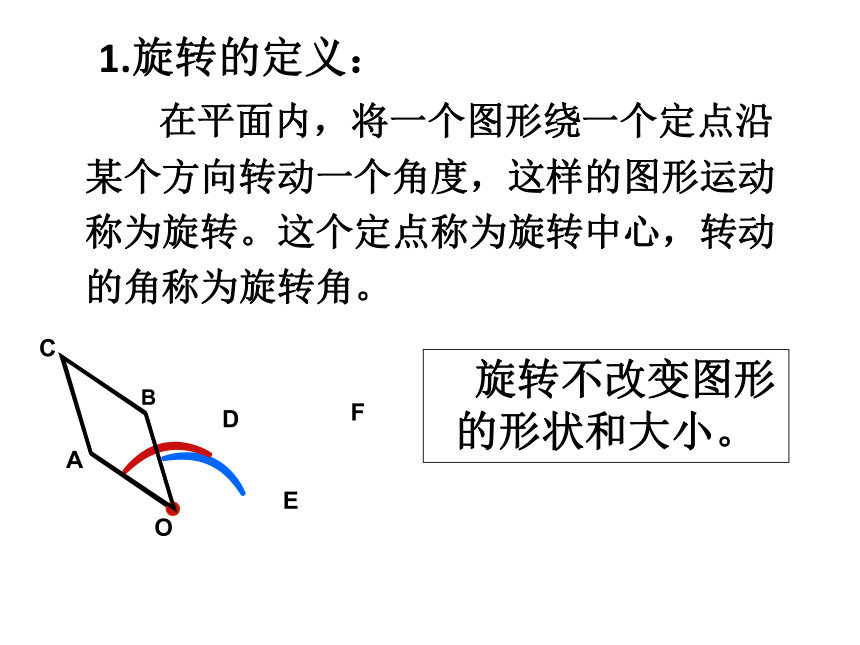
︵FABCDEO 旋转不改变图形的形状和大小。 1.旋转的定义:
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。 下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
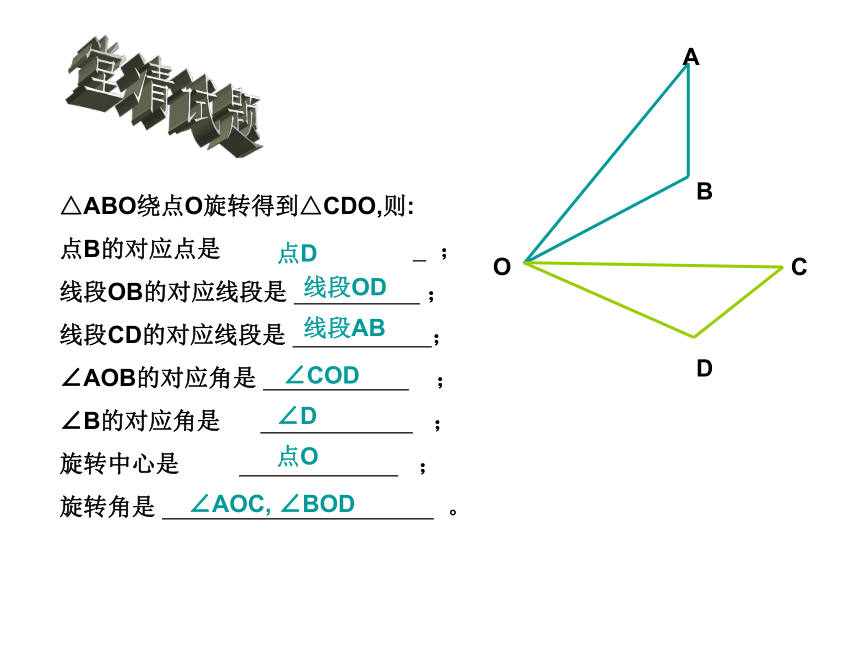
A.2 B.3 C.4 D.5 练一练ABOCD△ABO绕点O旋转得到△CDO,则:
点B的对应点是 ;
线段OB的对应线段是 ;
线段CD的对应线段是 ;
∠AOB的对应角是 ;
∠B的对应角是 ;
旋转中心是 ;
旋转角是 。堂清试题点D线段OD线段AB∠COD∠D点O∠AOC, ∠BOD动态演示OP′P 钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心是( )
(2)经过20分钟,分针旋转了( )度?想一想点O1. 任意一对对应点与旋转中心的连线所成的角都是旋转角。
2. 对应点到旋转中心的距离相等。
3. 旋转后的图形与原图形全等。
(旋转不改变图形的形状和大小)2.你能否观察发现旋转的性质?例1、 如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系? BO 与 EO 呢?
(4)∠AOD与∠BOE有什么大小关系?
例2、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?研讨应用解 (1)旋转中心是点A.(3)点M 转到了AC的中点位置上 图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?拓展练习1 答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.拓展练习2:
下图可看作是一个等腰直角三角形通过几次旋转得到的?每次旋转多少度? 答:旋转7次得到,旋转角度分别等于45°, 90°, 135°, 180°, 225°, 270 °,315°. 通过本节课的学习,请你来谈谈你的收获吧!一、这节课老师教给了你们什么?
二、这节课学到了些什么?
三、你们还有什么疑问需要老师给你们解决??知识点归纳1. 旋转的定义:“四要素”
一个图形、一个定点、一个方向、一个角度.
2. 旋转的性质:“三特点”
对应点与旋转中心的连线所成的角都是旋转角;
对应点到旋转中心的距离相等;
旋转不改变图形的形状和大小。
3. 旋转图形的形成描述:“五说明”
基本图形、旋转中心、方向、次数、旋转角.
“四、三、五”再见!
2.理解旋转的性质. 以上情景中的转动现象,有什么共同特征? 钟表的指针在转动过程中,其形状、
大小、位置是否发生改变?
飞机的螺旋桨、电风扇的叶轮的转动呢?观察思考︵
︵FABCDEO 旋转不改变图形的形状和大小。 1.旋转的定义:
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。 下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5 练一练ABOCD△ABO绕点O旋转得到△CDO,则:
点B的对应点是 ;
线段OB的对应线段是 ;
线段CD的对应线段是 ;
∠AOB的对应角是 ;
∠B的对应角是 ;
旋转中心是 ;
旋转角是 。堂清试题点D线段OD线段AB∠COD∠D点O∠AOC, ∠BOD动态演示OP′P 钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心是( )
(2)经过20分钟,分针旋转了( )度?想一想点O1. 任意一对对应点与旋转中心的连线所成的角都是旋转角。
2. 对应点到旋转中心的距离相等。
3. 旋转后的图形与原图形全等。
(旋转不改变图形的形状和大小)2.你能否观察发现旋转的性质?例1、 如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系? BO 与 EO 呢?
(4)∠AOD与∠BOE有什么大小关系?
例2、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?研讨应用解 (1)旋转中心是点A.(3)点M 转到了AC的中点位置上 图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?拓展练习1 答:旋转5次得到,旋转角度分别等于60°, 120°, 180°, 240°, 300°.拓展练习2:
下图可看作是一个等腰直角三角形通过几次旋转得到的?每次旋转多少度? 答:旋转7次得到,旋转角度分别等于45°, 90°, 135°, 180°, 225°, 270 °,315°. 通过本节课的学习,请你来谈谈你的收获吧!一、这节课老师教给了你们什么?
二、这节课学到了些什么?
三、你们还有什么疑问需要老师给你们解决??知识点归纳1. 旋转的定义:“四要素”
一个图形、一个定点、一个方向、一个角度.
2. 旋转的性质:“三特点”
对应点与旋转中心的连线所成的角都是旋转角;
对应点到旋转中心的距离相等;
旋转不改变图形的形状和大小。
3. 旋转图形的形成描述:“五说明”
基本图形、旋转中心、方向、次数、旋转角.
“四、三、五”再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
