第一章 三角函数单元综合检测题三(带解析)
文档属性
| 名称 | 第一章 三角函数单元综合检测题三(带解析) |  | |
| 格式 | zip | ||
| 文件大小 | 749.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-08 09:05:53 | ||
图片预览



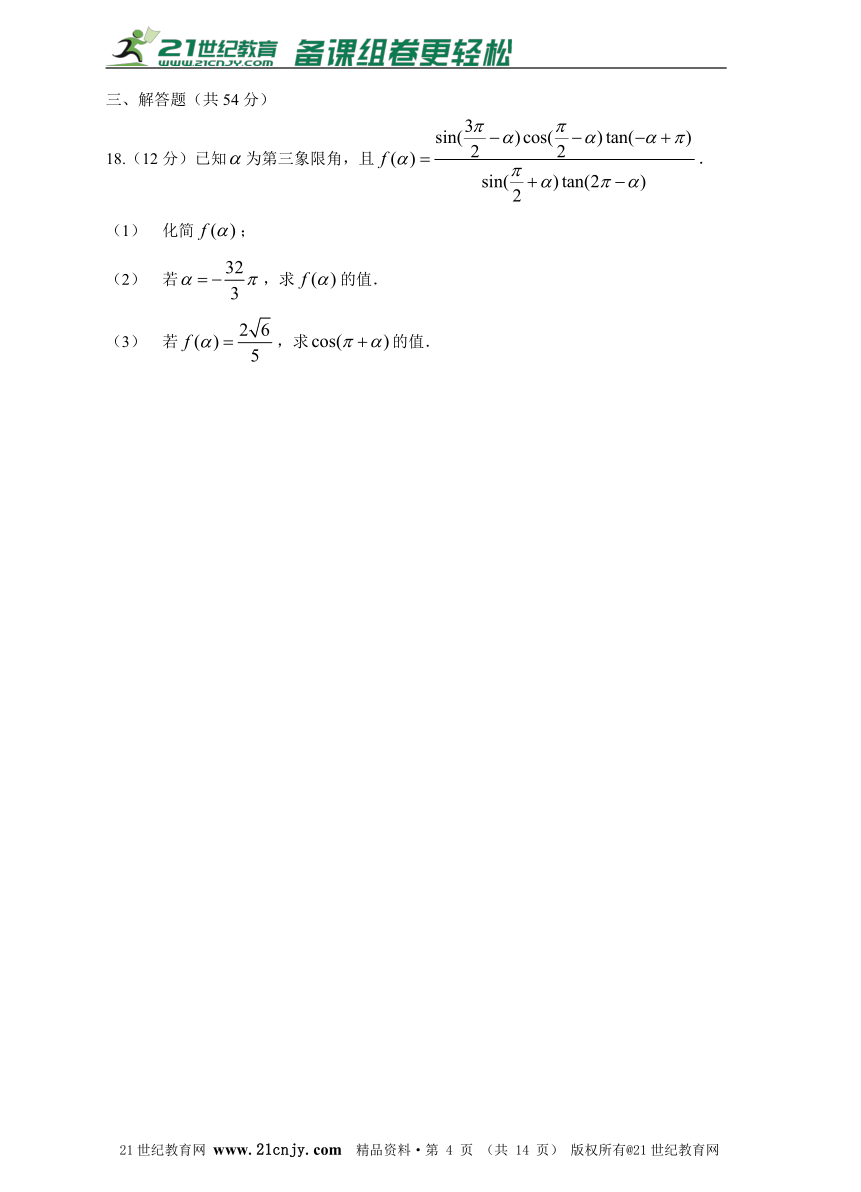

文档简介
第一章 三角函数单元综合检测题三(带解析)
一、选择题(共66分)
1.是( )
第一象限角 第二象限角 第三象限角 第四象限角
2.已知α,β为锐角,且cosα=,cosβ=,则α+β的值是( )
A. B. C. D.
3.已知角α的终边经过点(),则角α的最小正值是( )
A. B. C. D.
4.已知,则化简的结果为( )
A. B. C. D.以上都不对
5.已知,则的值为( ).
A. B. C. D.
6.下列坐标所表示的点不是函数的图象的对称中心的是 ( )
A. B. C. D.
7.下列函数中是奇函数,且最小正周期是的函数是( )
A.
B.
C.
D.
8.如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为( )
A. B. C. D.
9.下列函数中,最小正周期为的是( )
A. B. C. D.
10.已知函数,下列结论中错误的是
A.既偶函数,又是周期函数.
B.的最大值为
C.的图像关于直线对称
D.的图像关于中心对称
11.已知函数的图像如图所示,则函数的解析式是( )
A.
B.
C.
D.
二、填空题(共30分)
12.已知,则sinθ?cosθ=??? .
13.已知,则__________.
14.已知则的值为??? .
15.如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为,则cosα=??? .21教育网
16.已知函数y=Asin(ωx+φ)+n的最大值为4,最小值为0,最小正周期为,直线是其图象的一条对称轴,若A>0,ω>0,0<φ<,则函数的解析式为 .www.21-cn-jy.com
17.定义运算a*b为:,例如,1*2=1,则函数f(x)=sinx*cosx的值域为 ??? .
三、解答题(共54分)
18.(12分)已知为第三象限角,且.
(1) 化简;
(2) 若,求的值.
(3) 若,求的值.
19.(12分) 已知函数,且.
(1)求函数的最大值以及取得最大值时的集合;
(2)求函数的最小正周期和单调递增区间.
20.(15分)如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2. (1)用a,θ表示S1和S2; (2)当a固定,θ变化时,求取最小值时的角.21世纪教育网版权所有
21.(15分)已知,
(Ⅰ)求图象的对称轴方程;
(Ⅱ)若将函数的图象向右个单位长度后得到函数的图象,请写出函数的解析式;
(Ⅲ)请通过列表、描点、连线,在所给的平面直角坐标系中画出函数在上的简图.
参考答案及解析
1.D
∴sinα=-, ∴α=2kπ-或α=2kπ+,k∈Z, 又α是第四象限的角, ∴α=2kπ-, 令k=1,得角α的最小正值是. 4.A21·cn·jy·com
【解析】
5.B
【解析】
.
6.C
【解析】的对称中心为,所以的对称中心可以表示为,经检验C选项不满足条件,故选C.
7.D
【解析】函数是奇函数但周期是,故答案A错误。函数周期是,但是偶函数,故答案B错误。函数的周期为,但为偶函数,故答案C错误。函数是奇函数且周期为,故答案D正确。
8.A
【解析】先根据函数y=3cos(2x+ρ)的图象关于点中心对称,令x=代入函数使其等于0,求出ρ的值,进而可得|ρ|的最小值. ∵函数y=3cos(2x+φ)的图象关于点中心对称. ∴∴由此易得. 9.B2·1·c·n·j·y
【解析】根据三角函数的周期性可知正弦、余弦型最小正周期为T=,正切型最小正周期为
,
,
又,,故选C.
12.-
【解析】把已知的等式两边平方,利用同角三角函数的基本关系即可求得sinθcosθ的值. ∵已知,平方可得1+2sinθcosθ=,解得sinθcosθ=-, 点评:本题主要考查同角三角函数的基本关系的应用,属于基础题.【来源:21·世纪·教育·网】
13.2
【解析】因为,则
14.-
【解析】利用三角函数的转化进行求解 =cos()=-sin()=- 15.-
【解析】由三角函数的定义知sinα的值,由平方关系得cos2α,再由α角终边确定cosα的正负. 17.[-1,]21cnjy.com
【解析】依据题意可知首先看sinx≥cosx时,x的范围,进而求得函数的表达式,根据余弦函数的性质求得最大和最小值;再时,x的范围,进而求得函数的表达式sinx≤cosx,根据正弦函数的性质求得最大和最小值,最后综合可得答案. 当x∈[2k+,2kπ]时,sinx≥cosx,f(x)=cosx, 当x∈[2k+,2kπ+π]时此时函数的最大值为f(+2kπ)=,最小值为f()=-1 当x∈[2kπ,2kπ+]和x∈[2k+π,2kπ+2π]时sinx≤cosx,则f(x)=sinx,函数的最大值为f(+2kπ)=, 最小值为f(+2kπ)=- 最后综合可知函数的值域为[-1,] (3),21·世纪*教育网
又为第三象限角,
,
.
19.(1);;
(2);;
【解析】(1)由可得,确定函数解析式为,当取得最大值时,解出即可。注意写成集合形式。(2)整体思想。要求函数的增区间,只需,解出即可。注意最后必须写成区间形式。www-2-1-cnjy-com
(1) ,
用BQ+QR+RC=a列出方程求出x,算出S2; (2)由比值 称为“规划合理度”,可设t=sin2θ来化简求出S1与S2的比值,利用三角函数的增减性求出比值的最小值即可求出此时的θ. (1)在Rt△ABC中,AB=acosθ,AC=asinθ, 设正方形的边长为x则 , 由BP+AP=AB,得 ,故 所以 (2), 令t=sin2θ,因为 , 所以0<2θ<π,则t=sin2θ∈(0,1](10分) 所以 ,, 所以函数g(t)在(0,1]上递减,(11分) 因此当t=1时g(t)有最小值 , 此时 (Ⅲ)因为,所以.2-1-c-n-j-y
列表如下: 21*cnjy*com
描点、连线,得出所要求作的图象如下:
一、选择题(共66分)
1.是( )
第一象限角 第二象限角 第三象限角 第四象限角
2.已知α,β为锐角,且cosα=,cosβ=,则α+β的值是( )
A. B. C. D.
3.已知角α的终边经过点(),则角α的最小正值是( )
A. B. C. D.
4.已知,则化简的结果为( )
A. B. C. D.以上都不对
5.已知,则的值为( ).
A. B. C. D.
6.下列坐标所表示的点不是函数的图象的对称中心的是 ( )
A. B. C. D.
7.下列函数中是奇函数,且最小正周期是的函数是( )
A.
B.
C.
D.
8.如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为( )
A. B. C. D.
9.下列函数中,最小正周期为的是( )
A. B. C. D.
10.已知函数,下列结论中错误的是
A.既偶函数,又是周期函数.
B.的最大值为
C.的图像关于直线对称
D.的图像关于中心对称
11.已知函数的图像如图所示,则函数的解析式是( )
A.
B.
C.
D.
二、填空题(共30分)
12.已知,则sinθ?cosθ=??? .
13.已知,则__________.
14.已知则的值为??? .
15.如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为,则cosα=??? .21教育网
16.已知函数y=Asin(ωx+φ)+n的最大值为4,最小值为0,最小正周期为,直线是其图象的一条对称轴,若A>0,ω>0,0<φ<,则函数的解析式为 .www.21-cn-jy.com
17.定义运算a*b为:,例如,1*2=1,则函数f(x)=sinx*cosx的值域为 ??? .
三、解答题(共54分)
18.(12分)已知为第三象限角,且.
(1) 化简;
(2) 若,求的值.
(3) 若,求的值.
19.(12分) 已知函数,且.
(1)求函数的最大值以及取得最大值时的集合;
(2)求函数的最小正周期和单调递增区间.
20.(15分)如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2. (1)用a,θ表示S1和S2; (2)当a固定,θ变化时,求取最小值时的角.21世纪教育网版权所有
21.(15分)已知,
(Ⅰ)求图象的对称轴方程;
(Ⅱ)若将函数的图象向右个单位长度后得到函数的图象,请写出函数的解析式;
(Ⅲ)请通过列表、描点、连线,在所给的平面直角坐标系中画出函数在上的简图.
参考答案及解析
1.D
∴sinα=-, ∴α=2kπ-或α=2kπ+,k∈Z, 又α是第四象限的角, ∴α=2kπ-, 令k=1,得角α的最小正值是. 4.A21·cn·jy·com
【解析】
5.B
【解析】
.
6.C
【解析】的对称中心为,所以的对称中心可以表示为,经检验C选项不满足条件,故选C.
7.D
【解析】函数是奇函数但周期是,故答案A错误。函数周期是,但是偶函数,故答案B错误。函数的周期为,但为偶函数,故答案C错误。函数是奇函数且周期为,故答案D正确。
8.A
【解析】先根据函数y=3cos(2x+ρ)的图象关于点中心对称,令x=代入函数使其等于0,求出ρ的值,进而可得|ρ|的最小值. ∵函数y=3cos(2x+φ)的图象关于点中心对称. ∴∴由此易得. 9.B2·1·c·n·j·y
【解析】根据三角函数的周期性可知正弦、余弦型最小正周期为T=,正切型最小正周期为
,
,
又,,故选C.
12.-
【解析】把已知的等式两边平方,利用同角三角函数的基本关系即可求得sinθcosθ的值. ∵已知,平方可得1+2sinθcosθ=,解得sinθcosθ=-, 点评:本题主要考查同角三角函数的基本关系的应用,属于基础题.【来源:21·世纪·教育·网】
13.2
【解析】因为,则
14.-
【解析】利用三角函数的转化进行求解 =cos()=-sin()=- 15.-
【解析】由三角函数的定义知sinα的值,由平方关系得cos2α,再由α角终边确定cosα的正负. 17.[-1,]21cnjy.com
【解析】依据题意可知首先看sinx≥cosx时,x的范围,进而求得函数的表达式,根据余弦函数的性质求得最大和最小值;再时,x的范围,进而求得函数的表达式sinx≤cosx,根据正弦函数的性质求得最大和最小值,最后综合可得答案. 当x∈[2k+,2kπ]时,sinx≥cosx,f(x)=cosx, 当x∈[2k+,2kπ+π]时此时函数的最大值为f(+2kπ)=,最小值为f()=-1 当x∈[2kπ,2kπ+]和x∈[2k+π,2kπ+2π]时sinx≤cosx,则f(x)=sinx,函数的最大值为f(+2kπ)=, 最小值为f(+2kπ)=- 最后综合可知函数的值域为[-1,] (3),21·世纪*教育网
又为第三象限角,
,
.
19.(1);;
(2);;
【解析】(1)由可得,确定函数解析式为,当取得最大值时,解出即可。注意写成集合形式。(2)整体思想。要求函数的增区间,只需,解出即可。注意最后必须写成区间形式。www-2-1-cnjy-com
(1) ,
用BQ+QR+RC=a列出方程求出x,算出S2; (2)由比值 称为“规划合理度”,可设t=sin2θ来化简求出S1与S2的比值,利用三角函数的增减性求出比值的最小值即可求出此时的θ. (1)在Rt△ABC中,AB=acosθ,AC=asinθ, 设正方形的边长为x则 , 由BP+AP=AB,得 ,故 所以 (2), 令t=sin2θ,因为 , 所以0<2θ<π,则t=sin2θ∈(0,1](10分) 所以 ,, 所以函数g(t)在(0,1]上递减,(11分) 因此当t=1时g(t)有最小值 , 此时 (Ⅲ)因为,所以.2-1-c-n-j-y
列表如下: 21*cnjy*com
描点、连线,得出所要求作的图象如下:
