人教版数学八年级下册课件18.1.1 平行四边形的定义及性质 (共16张PPT)
文档属性
| 名称 | 人教版数学八年级下册课件18.1.1 平行四边形的定义及性质 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 961.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-10 16:15:25 | ||
图片预览





文档简介
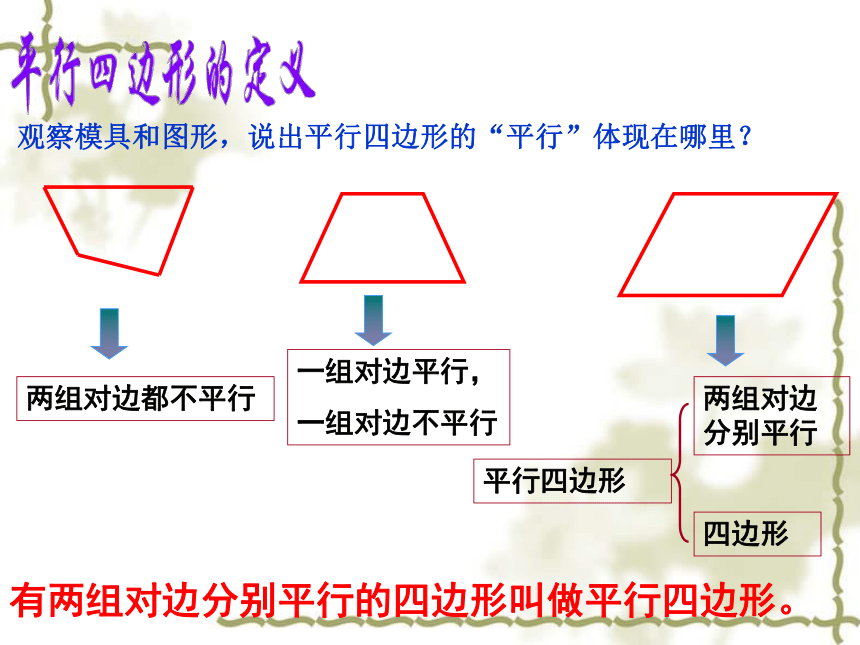
课件16张PPT。 凸四边形 凹四边形四边形的特性:1、有 条边、 个角;
2、内角和= °。第十八章
平行四边形
18.1.1 平行四边形的定义及性质举例:现实生活中的平行四边形?学习目标:1、记住平行四边形的相关概念;2、探究平行四边形的性质,会添加辅助线证明性质;3、记住性质并能应用性质解决简单的计算;4、进一步发展合情推理和演绎推理能力,增强几何直观和几何符号意识。两组对边都不平行一组对边平行,
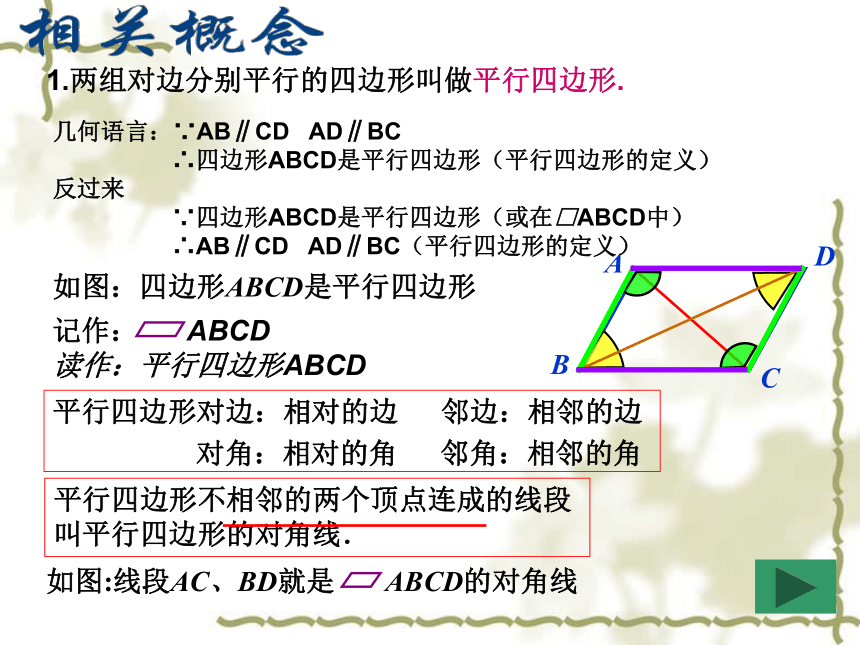
一组对边不平行有两组对边分别平行的四边形叫做平行四边形。观察模具和图形,说出平行四边形的“平行”体现在哪里? 平行四边形对边:相对的边 邻边:相邻的边
对角:相对的角 邻角:相邻的角1.两组对边分别平行的四边形叫做平行四边形.几何语言:∵AB∥CD AD∥BC
∴四边形ABCD是平行四边形(平行四边形的定义)
反过来
∵四边形ABCD是平行四边形(或在□ABCD中)
∴AB∥CD AD∥BC(平行四边形的定义)探究平行四边形的性质1、平行四边形除了内角和是360°、两组对边分别平行外,还有没有其它性质?
2、画一个 ABCD
3、度量对边AB与CD的长,BC与DA的长,可得什么结论?
AB=CD BC=DA 对边相等
4、度量对角∠A与∠C, ∠B与∠D的大小,可得什么结论?
∠A=∠C ∠B=∠D ∠A+ ∠B=180°
对角相等 邻角互补平行四边形的对边相等、对角相等?怎样证明?证明:连接AC在□ ABCD中,AD∥BC、AB∥CD( )∴∠1=∠2,∠3=∠4( )∴AD=BC,AB=CD,∠B=∠D( )又∵∠1=∠2,∠3 =∠4
∴ ∠1+∠3= ∠2 +∠4
即∠BAD=∠BCD求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.平行四边形的定义两直线平行,内错角相等在△ABC和△CDA中 ∴△ABC≌ △CDA (ASA) 全等三角形的对应边、对应角相等思考:不添加辅助线你能证明平行四边形的对角相等吗?性质1:平行四边形的对边相等.几何语言:
∵四边形ABCD为平行四边形
∴∠A=∠C,∠B=∠D.
周长: 面积:性质2:平行四边形的对角相等.几何语言:
∵四边形ABCD为平行四边形
∴AB=CD,AD=BC.性质应用例:如图,在若∠A=130°,则∠B=_____、∠C=____、∠D=____若∠A+ ∠C= 200°,则∠A=______ 、∠B=______若∠A:∠B= 5:4,则∠C=______ 、∠D=______50°130°50°100°80°100°80°返回若AB=1㎝,BC=2 ㎝6cm5cm若AB:BC=3:4,周长为14㎝,则CD=——,DA=——3cm4cm平行四边形定义:1、边:2、角:内角和等于360°
对角相等,
邻角互补3、周长:两邻边之和×2对边平行且相等4、面积:边长×边长上的高课堂小结有两组对边分别平行的平行四边形。性质:相关的几何符号语言、转化思想。
证明平行、线段相等、角相等的新方法。课后作业
P43第1题、第2题
P49第1题小试身手1、如图,在□ABCD中,根据已知填空,并说明理由。 ?∠A= ,∠C= ,∠D= ,
AD= CD= .120°60°120°10810米、8米、10米例:如图在若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____8cm28cm返回性质应用选择:∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3连接AC,若∠D=80°, ∠DAC=40°则, ∠B=___ ∠BAC=____,80°60°B综合发散AB=5,BC=9,BE平分∠ABC,
4如图,则DE= _________123返回ABCD如图, □ ABCD中,BC=5,AC=4,
∠BAC=90.则□ ABCD的面积为 12543返回
2、内角和= °。第十八章
平行四边形
18.1.1 平行四边形的定义及性质举例:现实生活中的平行四边形?学习目标:1、记住平行四边形的相关概念;2、探究平行四边形的性质,会添加辅助线证明性质;3、记住性质并能应用性质解决简单的计算;4、进一步发展合情推理和演绎推理能力,增强几何直观和几何符号意识。两组对边都不平行一组对边平行,
一组对边不平行有两组对边分别平行的四边形叫做平行四边形。观察模具和图形,说出平行四边形的“平行”体现在哪里? 平行四边形对边:相对的边 邻边:相邻的边
对角:相对的角 邻角:相邻的角1.两组对边分别平行的四边形叫做平行四边形.几何语言:∵AB∥CD AD∥BC
∴四边形ABCD是平行四边形(平行四边形的定义)
反过来
∵四边形ABCD是平行四边形(或在□ABCD中)
∴AB∥CD AD∥BC(平行四边形的定义)探究平行四边形的性质1、平行四边形除了内角和是360°、两组对边分别平行外,还有没有其它性质?
2、画一个 ABCD
3、度量对边AB与CD的长,BC与DA的长,可得什么结论?
AB=CD BC=DA 对边相等
4、度量对角∠A与∠C, ∠B与∠D的大小,可得什么结论?
∠A=∠C ∠B=∠D ∠A+ ∠B=180°
对角相等 邻角互补平行四边形的对边相等、对角相等?怎样证明?证明:连接AC在□ ABCD中,AD∥BC、AB∥CD( )∴∠1=∠2,∠3=∠4( )∴AD=BC,AB=CD,∠B=∠D( )又∵∠1=∠2,∠3 =∠4
∴ ∠1+∠3= ∠2 +∠4
即∠BAD=∠BCD求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.平行四边形的定义两直线平行,内错角相等在△ABC和△CDA中 ∴△ABC≌ △CDA (ASA) 全等三角形的对应边、对应角相等思考:不添加辅助线你能证明平行四边形的对角相等吗?性质1:平行四边形的对边相等.几何语言:
∵四边形ABCD为平行四边形
∴∠A=∠C,∠B=∠D.
周长: 面积:性质2:平行四边形的对角相等.几何语言:
∵四边形ABCD为平行四边形
∴AB=CD,AD=BC.性质应用例:如图,在若∠A=130°,则∠B=_____、∠C=____、∠D=____若∠A+ ∠C= 200°,则∠A=______ 、∠B=______若∠A:∠B= 5:4,则∠C=______ 、∠D=______50°130°50°100°80°100°80°返回若AB=1㎝,BC=2 ㎝6cm5cm若AB:BC=3:4,周长为14㎝,则CD=——,DA=——3cm4cm平行四边形定义:1、边:2、角:内角和等于360°
对角相等,
邻角互补3、周长:两邻边之和×2对边平行且相等4、面积:边长×边长上的高课堂小结有两组对边分别平行的平行四边形。性质:相关的几何符号语言、转化思想。
证明平行、线段相等、角相等的新方法。课后作业
P43第1题、第2题
P49第1题小试身手1、如图,在□ABCD中,根据已知填空,并说明理由。 ?∠A= ,∠C= ,∠D= ,
AD= CD= .120°60°120°10810米、8米、10米例:如图在若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____8cm28cm返回性质应用选择:∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3连接AC,若∠D=80°, ∠DAC=40°则, ∠B=___ ∠BAC=____,80°60°B综合发散AB=5,BC=9,BE平分∠ABC,
4如图,则DE= _________123返回ABCD如图, □ ABCD中,BC=5,AC=4,
∠BAC=90.则□ ABCD的面积为 12543返回
