9.2 幂的乘方与积的乘方

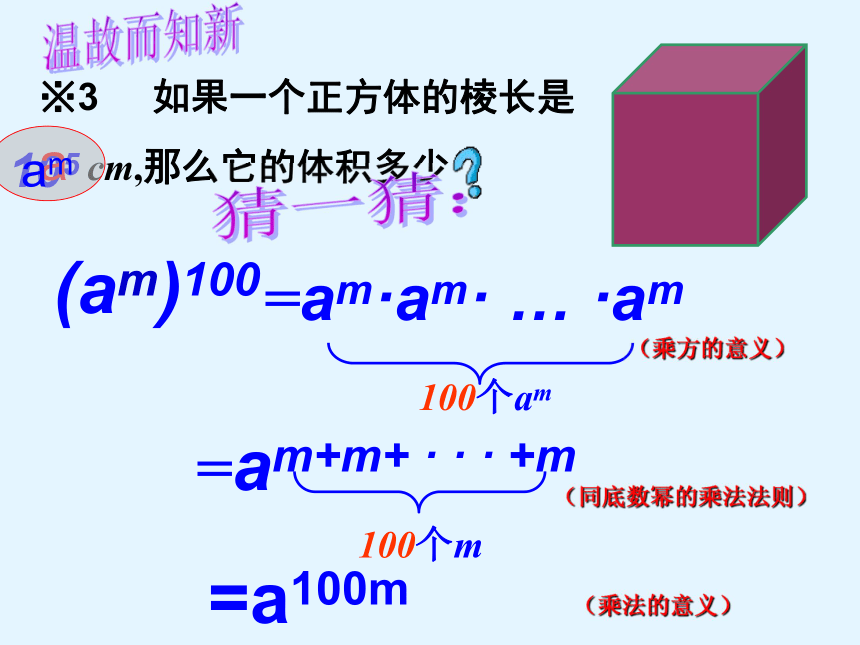
课件16张PPT。8.2幂的乘方与积的乘方(1)am · an= am+nan=am · an=am+n（m , n都是正整数）推导：温故而知新同底数幂的乘法※2※1幂的意义※3 如果一个正方体的棱长是
cm,那么它的体积多少
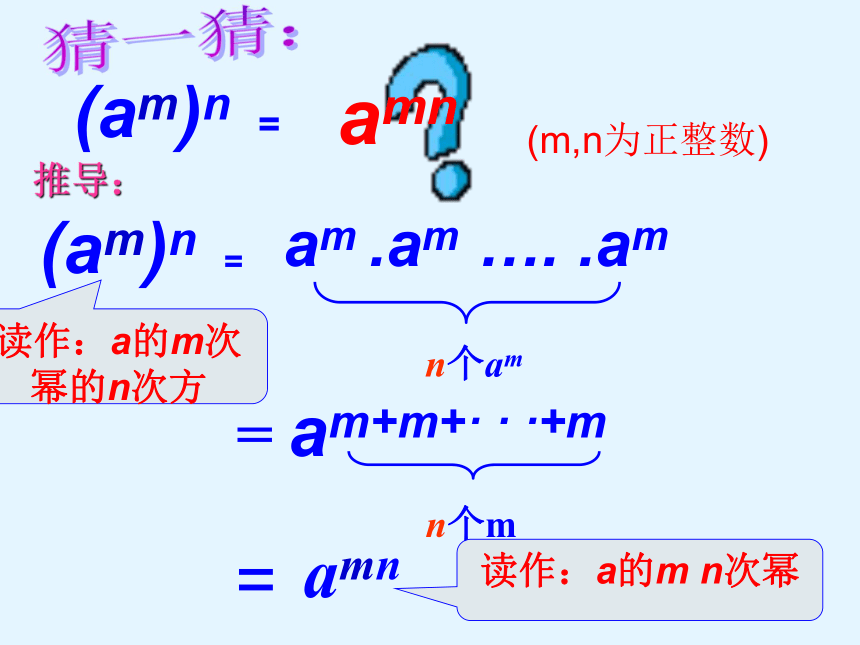
100个m=am+m+ · · · +m100个am105a am猜一猜：=am·am· … ·am=a100m(am)100温故而知新（乘方的意义）（同底数幂的乘法法则）（乘法的意义）amn n个m= am+m+· · ·+mn个am猜一猜：am .am …. .am读作：a的m次幂的n次方=(am)n =读作：a的m n次幂(am)n =amn(m,n为正整数)推导：(am)n = amn (m,n都是正整数)底数 , 幂的乘方，不变相乘结论：幂 的 乘 方的运算 法 则:指数 . 用语言叙述：公式的应用【例1】计算： (4) (－ x6+m)3 =解：(3)(－xm)2= xm×2=x2m(5) －(ym)n= － ym×n= － ymn- x(6+m) ×3=-x18+3m(6) [(x-y)m]3 = (x – y)3m(1)(106)20=106×20=10120(2)(y4)n= y4×n= y4n=(x-y)m×3幂的底数和指数不仅可以是单项式,也可以是多项式. (am)n = amn (m,n都是正整数)注意符号看谁答的快！1、判断并改正：
(a3)2 = a3+2 = a5 ( )
(2) (-a5)2 = - a10 ( )2、直接说出结果：××a6a10=1020 =m10a=x4n+8=(x-2y) 6m=-a10+5m=a28（1）下列各式中，与(xm+1)3相等的是（　　）
A. 3xm+1 B. x3m+x3
C. x3·xm+1 D. x3m·x3DC3、选择：(2). 9m·27n可以写为： ( )
A. 9m+3n B. 27m+n
C. 32m+3n D. 33m+2n
【例2】计算：[(am)n]p=幂的乘方的推导(amn)p=amnp（m,n,p为正整数）(am)n = amn (m,n都是正整数)
若 (am) n=am n=an m=(a m)n则 a mn=(a n)m公式的逆向应用例如:
x12=(x2)( ) =(x6)( )
=(x3)( ) =(x4)( )
=x7?x( ) =x?x( )6245113【例3】计算1、若am=2,an=3,求① am+n 的值。② a3m+2n的值。2、若9×27x = 34x+1，求x的值解：∵am=2,an=3∴a 3m+2n=a3m·a2n=(am)3·(an)2=23×32=72∴ am+n=am·an=2×3=6∴ 32 ×33x = 34x+1即 33x+2 = 34x+1∴ 3x+2 = 4x+1x = 1构建方程化归思想解： ∵ 9×27x = 34x+1逆用公式这节课，我的收获是---小结与回顾知识树(am)n = amn
am?an=am+n
例3:第2题公式应用这节课，我的收获是---例3:第1题习题《学与练》P31.四作业再 见思考题：3、比较3555 、4444 、5333的大小.