12.3 探索三角形全等的条件

课件23张PPT。11.3探索三角形全等的条件（一）说课稿 一 教材分析 二 教法及学法分析三 教学过程分析四 教学评价1、 教材的地位与作用 （1）本节《探索三角形全等的条件一》既是对前面所学的全等三角形的特征的延伸与拓展，又是后继学习探索相似三角形的条件的基础，并且是说明线段相等、两角相等的重要方法。因此，本节课的知识具有承上启下的作用，同时，苏科版教材将“边角边” 作为五个识别方法之首，说明本节的内容对学生学习三角形全等的识别具有举足轻重的作用。 （2）通过探索三角形全等的“边角边”条件，可以让学生了解研究数学问题的方法，感知数学知识的形成过程，领会数学思想，同时发展学生的空间想象能力，培养学生逻辑推理的能力。 教材分析教法及学法教学过程教学评价2、 教学目标（1） 知识与技能：
①掌握边角边的判定方法，会运用边角边判定方法证明两个三角形全等。
②掌握两边一角画三角形的方法。
③体会证明两线段相等，两个角相等可以转化为“证明两三角形全等”来解决的数学方法。（2）过程与方法：
从动手操作到理性证明探索出三角形全等的判定方法：“边角边”，通过“边角边”的应用，掌握转化的数学方法。（3）情感、态度与价值观：
①培养学生的动手实践能力。
②培养学生严密的逻辑推理能力。
教材分析教法及学法教学过程教学评价 3、 教学重点和难点 由于本节课是第一次探索三角形全等的条件，故我确立了以“探究全等三角形的必要条件的个数及探究边角边这一识别方法作为教学的重点，而将边角边，边边角的辨析和边角边的应用作为教学的难点。同时，我将采用让学生动手操作、合作探究、媒体演示的方式以及渗透分类讨论的数学思想方法来突出重点、突破难点。 教材分析教法及学法教学过程教学评价教材分析教法及学法教学过程教学评价教法及学法：遵循“学生为主体，教师为主导”的教学原则，按照学生从感性认识到理性认识，借助于多媒体课件演示及学生动手操作确认发现新知。启发式的引导学生展开思维、探究证明思路，规范几何语言的书学，循序渐进的教学方法。教学准备教法及学法教学评价教材分析教学过程
教师方面：课件、三角板、圆规
学生方面：三角板，圆规，剪刀，手工纸。
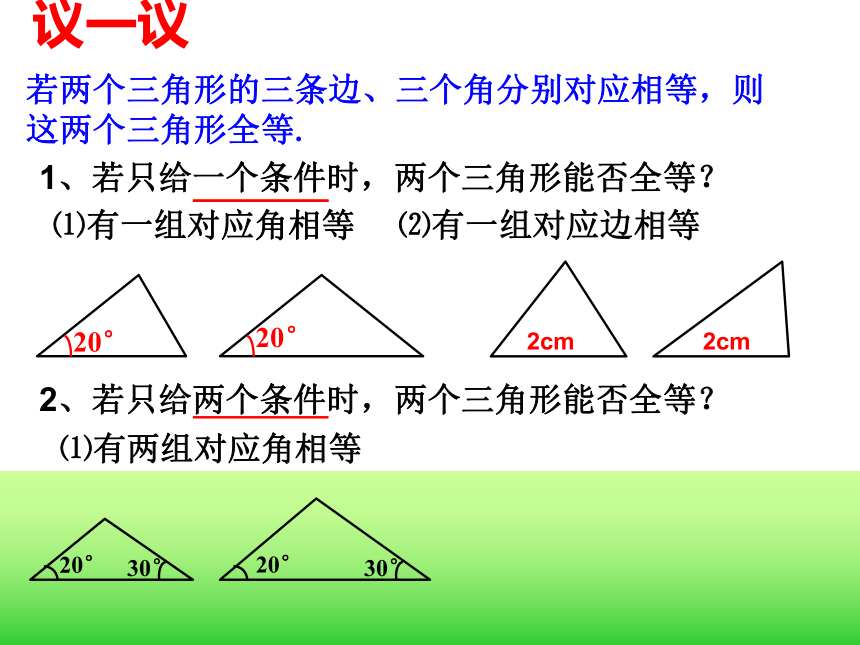
?先复习全等三角形的特征（全等三角形对应边，对应角相等）议一议1、若只给一个条件时，两个三角形能否全等？若两个三角形的三条边、三个角分别对应相等，则这两个三角形全等. ⑴有一组对应角相等 ⑵有一组对应边相等 2、若只给两个条件时，两个三角形能否全等？⑴有两组对应角相等 ⑵有一组对应角相等、一组对应边相等 议一议
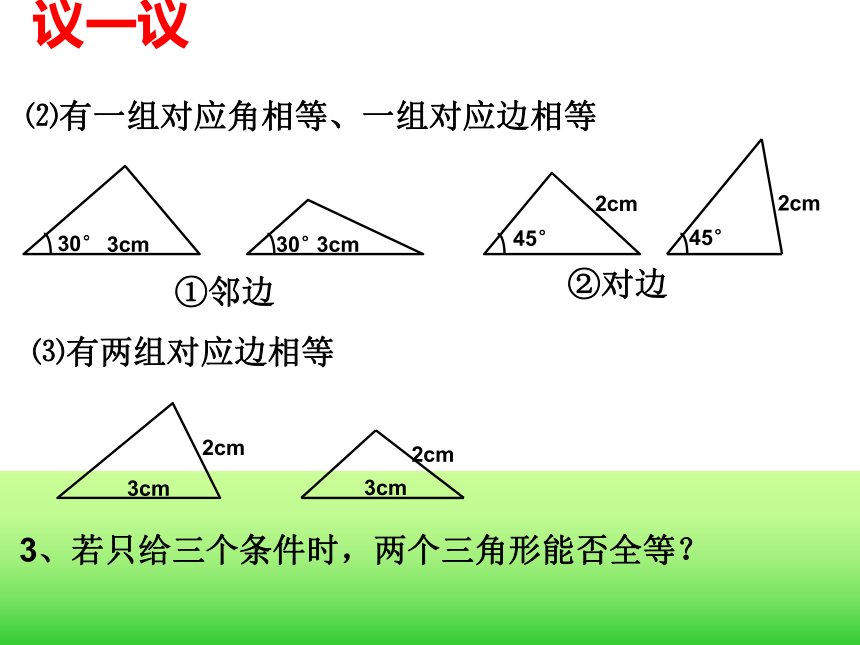
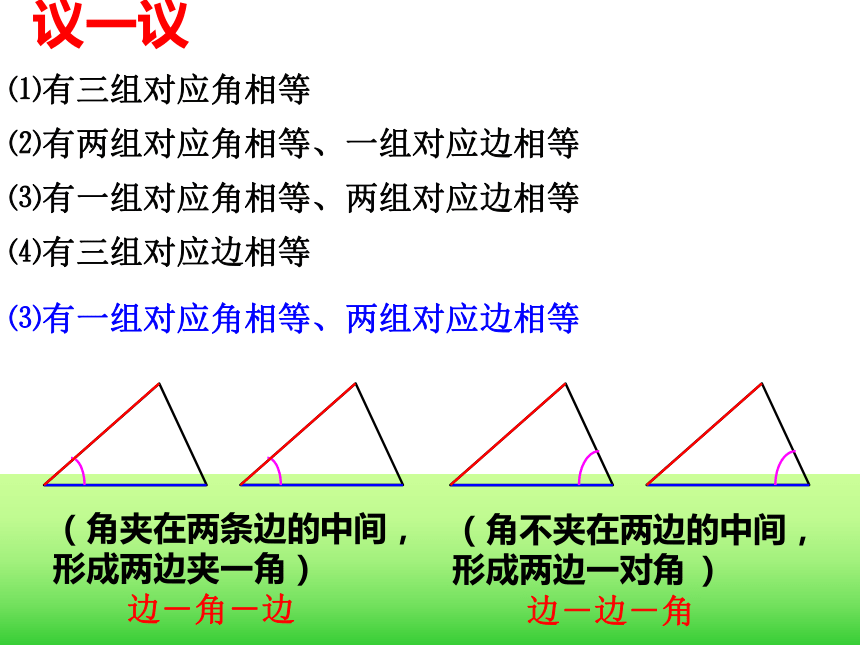
①邻边②对边⑶有两组对应边相等 3、若只给三个条件时，两个三角形能否全等？⑴有三组对应角相等 ⑵有两组对应角相等、一组对应边相等 ⑶有一组对应角相等、两组对应边相等 ⑷有三组对应边相等 议一议
⑶有一组对应角相等、两组对应边相等 边－角－边边－边－角（角夹在两条边的中间，形成两边夹一角） （角不夹在两边的中间，形成两边一对角 ） 探究新知⑴⑴边－角－边（角夹在两条边的中间，形成两边夹一角） 做一做已知两条线段和一个角，以这两条线段为边，以这个角为这两条边的夹角，画一个三角形． 步骤：　
1、画一线段AB，使它等于4cm；
2、画∠MAB＝45°；
3、在射线AM上截取AC＝3cm；
4、连结BC．
△ABC即为所求．ABMC4cm45°3cm探究新知⑵⑵边－边－角（角不夹在两边的中间，形成两边一对角 ） 做一做已知两条线段和一个角，以长的线段为已知角的邻边，短的线段为已知角的对边，画一个三角形． 步骤：　
1、画一线段AB,使它等于4cm ；
2、画∠ BAM= 45° ；
3、以B为圆心, 3cm长为半径画弧,交AM于点C ；
4、连结CB ．
△ABC即为所求．把你画的三角形与其他同学画的三角形进行比较，所有的三角形都全等吗？探究新知⑵ABMCD结论：两边及其一边所对的角相等，两
个三角形不能全等.把你画的三角形与其他同学画的三角形进行比较，所有的三角形都全等吗？如果两个三角形有两边及其夹角分别对应相等，那么这两个三角形全等．简记为SAS（或边角边）．三角形全等的判定方法（1）：几何语言：在△ABC与△DEF中AB=DE∠B=∠EBC=EF∴△ABC≌△DEF（SAS）探究新知⑴∵例题讲解例1如图，在△ABC中，AB＝AD， ∠BAD＝∠CAD ，△ABD和△ACD全等吗？为什么？．证明: 　 AD＝AD∴△ABD≌△ACD（SAS）在△ABD与△ACD中∵AB＝AC∠BAD＝∠CAD∴△ABD≌△ACD例题推广1、如图，在△ABC中，AB＝AC，AD平分∠BAC，求证： ∠B＝∠C ．证明: ∵∴　∠BAD＝∠CAD　 AD＝AD∴△ABD≌△ACD（SAS）∵　AD平分∠BAC在△ABD与△ACD中AB＝AC∠BAD＝∠CAD∴∠B＝∠C（全等三角形的对应角相等）利用“SAS”和“全等三角形的对应角相等”这两条公理证明两个角相等若题目的已知条件不变，你还能证得哪些结论？例题推广2、如图，在△ABC中，AB＝AC，AD平分∠BAC，求证： ．BD=CD证明: ∴BD＝CD（全等三角形的对应边相等）这就说明了点D是BC的中点，从而AD是底边BC上的中线。
1、在下列图中找出全等的三角形。
答案：1——3； 2——5； 4——6巩固训练2、根据题目条件，判断下面的三角形是否全等．
（1）　AC＝DF，∠C＝∠F，BC＝EF；
（2）　BC＝BD，∠ABC＝∠ABD．
(1)全等(2)全等巩固训练(1)(2)3、已知，如图，AB＝AC,AD=AE,
求证: △ABE ≌ △ACD.


ABCDE证明：在△ABE 和△ACD中，
∵ AB=AC
∠A= ∠A(公共角）
AD=AE
∴ △ABE ≌ △ACD.(S.A.S)巩固训练4、已知：如图，AB和CD相交于E ,EA=EB.ED=EC,求证：（1）△AED ≌ △BEC.
（2）∠D= ∠C
(3) AD=BC
证明：在△AED和△BEC中，
∵ EA=EB
∠AED= ∠BEC
ED=EC
∴ △AED ≌ △BEC（S.A.S)
∴ ∠D= ∠C （全等三角形对应角相等)
∴ AD=BC (全等三角形对应线段相等)巩固训练课堂小结今天你学到了什么?1、今天我们学习了哪种方法判定两个三角形全等？通过证明三角形全等可以证明两条线段相等等、两个角相等。答：SAS(边角边)（角夹在两条边的中间，形成两边夹一角） 2、 “边边角”能不能判定两个三角形全等？答：不能布置作业目标实验手册90页1-5. 本节课我将始终关注学生能否在老师的引导下积极主动地按所给的条件进行探索，能否在活动中大胆尝试并表达自己的想法从而发现结论。对不同的学生有不同的评价标准，尊重学生的个体差异，把评价贯穿于探索活动的全过程，发挥评价的功能，以帮助学生认识自我，建立信心，共同进步。教材分析教法及学法教学过程教学评价