图形的平移

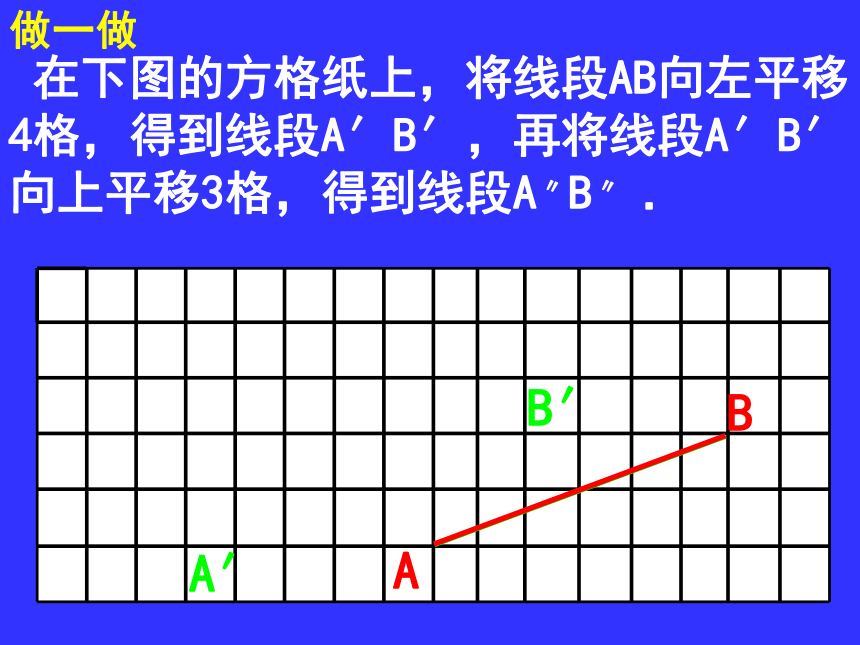
课件20张PPT。图形的平移（2） 在下图的方格纸上，将线段AB向左平移4格，得到线段A′B′，再将线段A′B′向上平移3格，得到线段A〃B〃 ．
做一做A′B′ 在下图的方格纸上，将线段AB向左平移4格，得到线段A′B′，再将线段A′B′向上平移3格，得到线段A〃B〃 ．
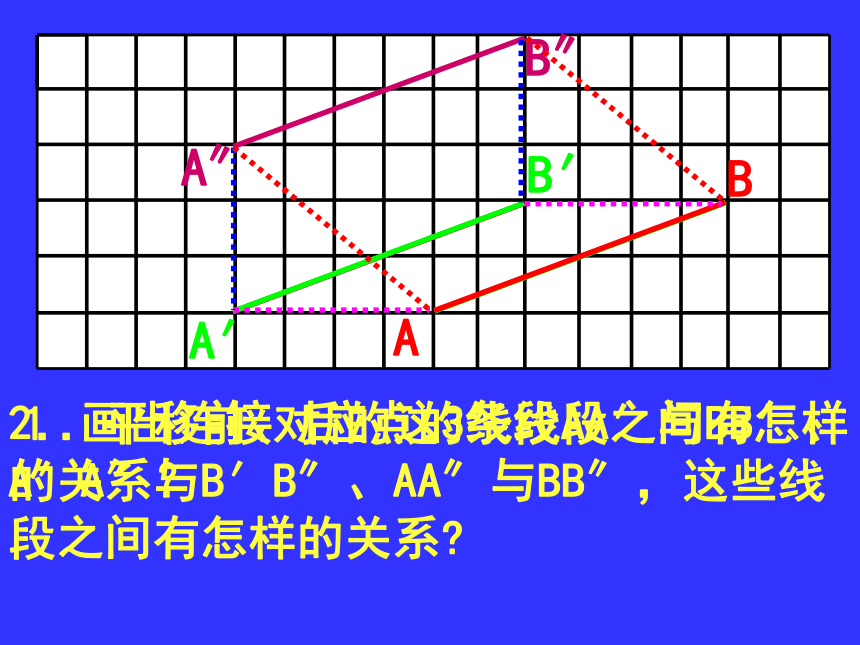
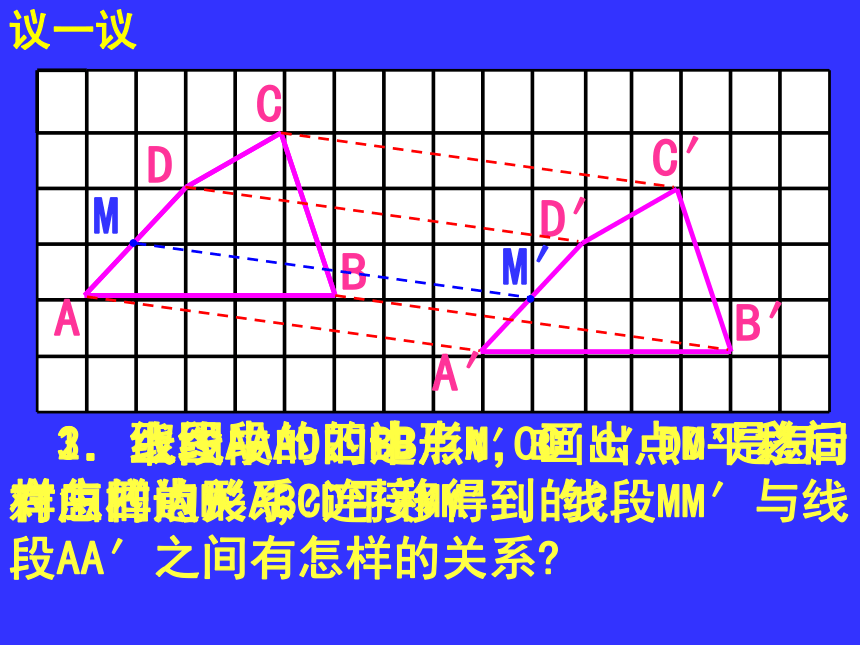
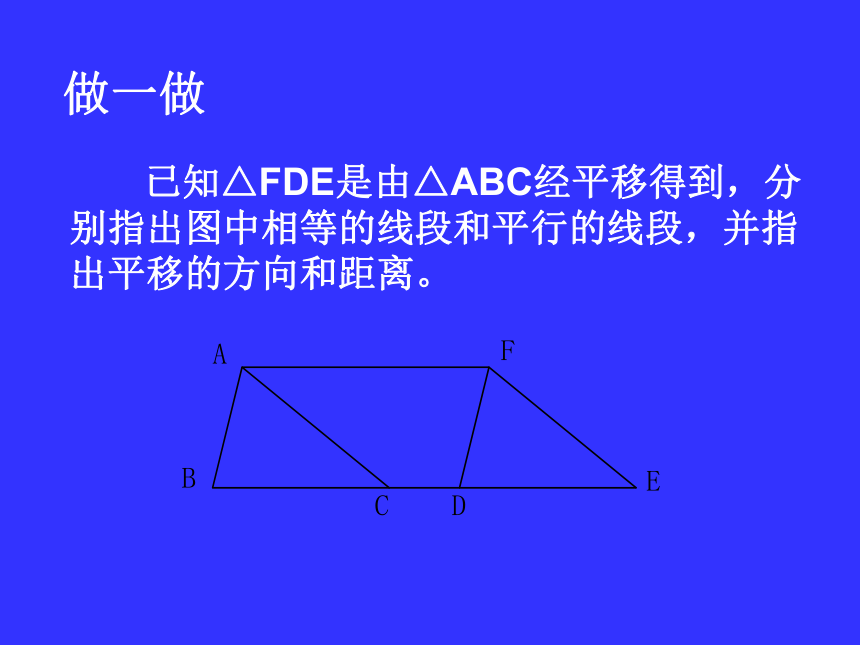
做一做A′B′A″B″A′B′A″B″１．平移前、后的这3条线段之间有怎样的关系？2．画出连接对应点的线段AA′与BB′、 A′A″与B′B″、AA″与BB″，这些线段之间有怎样的关系?议一议 1．上图中的四边形A′B′C′D′是怎样由四边形ABCD平移得到的?ABCDA′B′C′D′ 2．线段AA′、BB′、CC′、DD′之间有怎样的关系?　3．取线段AD的中点M，画出点M平移后对应的点M′，连接MM′．线段MM′与线段AA′之间有怎样的关系?M′ 1．上图中的线段MN是怎样由线段AB平移得到的? 2．线段AM与线段BN有什么关系呢? 图形经过平移，连接各组对应点所得的线段互相平行(或在同一条直线上)并且相等．图形平移的基本性质：做一做 已知△FDE是由△ABC经平移得到，分别指出图中相等的线段和平行的线段，并指出平移的方向和距离。平移的特征２： （１）若干次的平移都可以通过一次平移　　　达到同样的效果 将三角尺ABC沿直尺的一边b平移：AA′BB′CC′ab (1)三角尺的顶点A、B移动所形成的两条直线a、b是否平行?为什么? (2)在平移过程中，AC是否始终垂直于直线a、b ? 如图：直线a与直线b平行． (1)在直线a上任意取两点A、A′，分别过点A、A′作直线b的垂线，垂足分别为C、C′；ab．A′ (2)分别度量点A、A′到直线b的距离,你发现了什么?C′CA．． 如图：直线a与直线b不平行． (1)在直线a上任意取两点A、A′，分别过点A、A′作直线b的垂线，垂足分别为C、C′；ab．A′ (2)分别度量点A、A′到直线b的距离,你发现了什么?C′CA．． 定义：如果两条直线互相平行，那么其中一条直线上任意两点到另一条直线的距离相等，这个距离称为平行线之间的距离．例1 如图所示，在长方形ABCD中，AD=2AB，E、F分别为AD及BC的中点，扇形BFE、FCD的半径FB与CF的长度均为1cm，求阴影部分的面积.∴S阴影=S图形ABE+S扇形DFC
=S图形ABE+S扇形EBF
=S正方形ABFE
=AB·AE
=1(cm2)要正确利用图形平移，
巧妙求出阴影部分面积. 解:如图所示:
∵扇形EBF由扇形DFC平移得到例2:如图，先将两个直角梯形重叠在一起，再将其中一个直角梯形沿AD的方向平移，平移距离为AE长.求阴影部分面积(单位：厘米). 例3.如图，ABCD是一个长方形，E、F、G、H分别是边AD及BC边上的三等分点，图中矩形内的两条曲线都是图示的四分之一圆周.求阴影部分面积(单位：厘米).1.求图中阴影部分面积(单位：厘米).练习例2 如图，原来是重叠的两个直角三角形，将其中一个三角形沿着BC方向平移BE的距离，就得到此图形，求阴影部分面积(单位：厘米). 1264小结　　通过本节课的学习，你有何收获呢？　 (1)通过操作活动，探索了图形平移的基本性质：图形经过平移，连接各组对应点的线段平行(或在同一条直线上)并且相等； (2)通过操作活动，探索了两条直线平行的一个性质：若两条直线互相平行，则其中一条直线上任意两点到另一条直线的距离相等．