2.1.2 三角形高、角平分线、中线 课件
文档属性
| 名称 | 2.1.2 三角形高、角平分线、中线 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 491.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-09 20:27:52 | ||
图片预览





文档简介
课件12张PPT。1.由_______________的三条线段________
所构成的图形叫做三角形.2.____________的三角形叫做等腰三角形,
其中______________叫做腰,另一边
叫做_____.3.三角形的 ______ 大于第三边.不在同一直线上首尾相接两条边相等相等的两边底边任意两边之和 从三角形的一个顶点向它的对边所在的直
线作垂线,顶点和垂足之间的线段叫作三角形
的高线,简称三角形的高. 如图,AH⊥BC,垂足为点H,
则线段AH是△ABC的BC边上的高.如图,试画出图中△ABC的BC边上的高.D 在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线. 如图,∠BAD=∠CAD,
则线段AD是△ABC的一条角平分线. 在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线. 如图,BE=EC,
则线段AE是△ABC的BC边上的中线.想一想:
任何一个三角形有几条高?几条
角平分线?有几条中线? 请同学们猜想一下:
三角形的角平分线,中线,高分别有
几条?它们是在三角形内还是在三角形外?
答:三角形有三条角平分线,三条中
线,三条高. 三条角平分线和三条中线是
在三角形内,而三条高不一定都在三角形
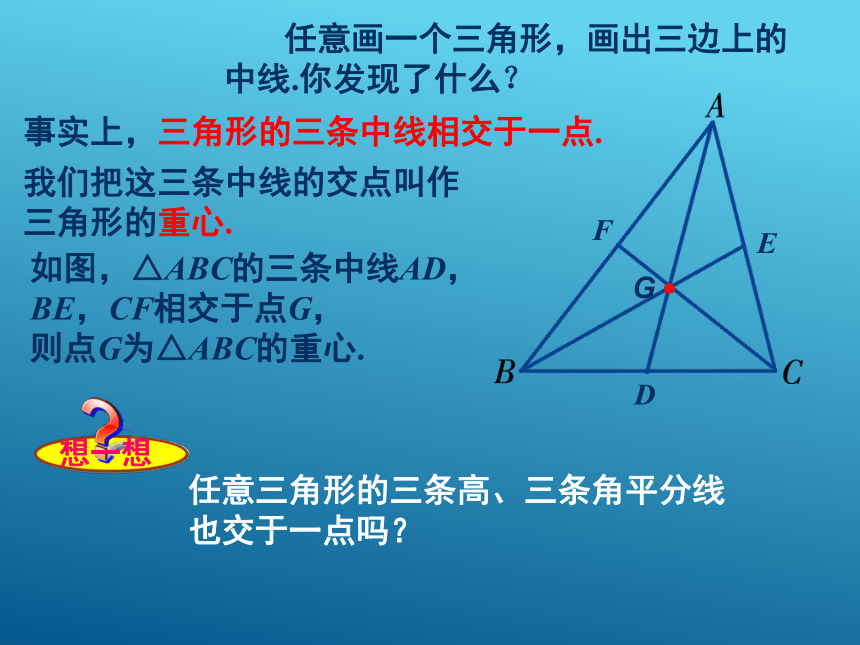
内,但至少有一条高是在三角形内. 任意画一个三角形,画出三边上的中线.你发现了什么?G事实上,三角形的三条中线相交于一点.我们把这三条中线的交点叫作
三角形的重心.如图,△ABC的三条中线AD,
BE,CF相交于点G,
则点G为△ABC的重心.任意三角形的三条高、三条角平分线
也交于一点吗?例2 如图AD是△ABC的中线,AE是△ABC的高.(1)图中共有几个三角形?请分别列举出来.解 (1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.(2)其中哪些三角形的面积相等?解 ∵AD是△ABC的中线,∴BD=DC. ∵AE是△ABC的高,也是△ABD和 △ADC的高, ∴S△ABD = S△ADC .三角形中线把三角形平分成面积相等的两部分.1. 利用三角尺(或直尺)、量角器任意画出一
个三角形,并画出其中一条边上的中线、高以
及这条边所对的角的平分线.2. 如图,AD是△ABC的高,DE是△ADB的中线,
BF是△EBD的角平分线,根据已知条件填空:ADC90AEABEBFDBE3.如图,AD,BE,CF 是△ABC
的三条角平分线,则:
∠1 = ; ∠3 = ;
∠ACB = 2 .∠2∠422BD6 cm2 4.如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ; AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .5、在ΔABC中,CD是中线,已知
BC-AC=5cm,ΔDBC的周长为25cm,
求ΔADC的周长. 1. 如图:AD,AE分别是△ABC的高和中线,且AB=8㎝ ,AC=6㎝,BC=10 cm,∠CAB=90°.试求:(1)AD的长;
(2)△ABE的面积;
(3)△ABE和△ACE的周长差.
(3) ∵ C△AEC =AC+CE+AE
C△ABE =AB+BE+AE ,
∴ C△AEC-C△ABE=AC+CE+AE-(AB+BE+AE)
=AC-AB=8-6=2 cm.
感悟与反思通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
有什么需要同学们帮助解决的问题吗?从知识上,在小学学习的基础上,我们又学习了什么?从方法上,我们是怎么认识这些重要线段的。对你后续的学习有什么启示吗?作业:P49 A 3 B 6
所构成的图形叫做三角形.2.____________的三角形叫做等腰三角形,
其中______________叫做腰,另一边
叫做_____.3.三角形的 ______ 大于第三边.不在同一直线上首尾相接两条边相等相等的两边底边任意两边之和 从三角形的一个顶点向它的对边所在的直
线作垂线,顶点和垂足之间的线段叫作三角形
的高线,简称三角形的高. 如图,AH⊥BC,垂足为点H,
则线段AH是△ABC的BC边上的高.如图,试画出图中△ABC的BC边上的高.D 在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线. 如图,∠BAD=∠CAD,
则线段AD是△ABC的一条角平分线. 在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线. 如图,BE=EC,
则线段AE是△ABC的BC边上的中线.想一想:
任何一个三角形有几条高?几条
角平分线?有几条中线? 请同学们猜想一下:
三角形的角平分线,中线,高分别有
几条?它们是在三角形内还是在三角形外?
答:三角形有三条角平分线,三条中
线,三条高. 三条角平分线和三条中线是
在三角形内,而三条高不一定都在三角形
内,但至少有一条高是在三角形内. 任意画一个三角形,画出三边上的中线.你发现了什么?G事实上,三角形的三条中线相交于一点.我们把这三条中线的交点叫作
三角形的重心.如图,△ABC的三条中线AD,
BE,CF相交于点G,
则点G为△ABC的重心.任意三角形的三条高、三条角平分线
也交于一点吗?例2 如图AD是△ABC的中线,AE是△ABC的高.(1)图中共有几个三角形?请分别列举出来.解 (1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.(2)其中哪些三角形的面积相等?解 ∵AD是△ABC的中线,∴BD=DC. ∵AE是△ABC的高,也是△ABD和 △ADC的高, ∴S△ABD = S△ADC .三角形中线把三角形平分成面积相等的两部分.1. 利用三角尺(或直尺)、量角器任意画出一
个三角形,并画出其中一条边上的中线、高以
及这条边所对的角的平分线.2. 如图,AD是△ABC的高,DE是△ADB的中线,
BF是△EBD的角平分线,根据已知条件填空:ADC90AEABEBFDBE3.如图,AD,BE,CF 是△ABC
的三条角平分线,则:
∠1 = ; ∠3 = ;
∠ACB = 2 .∠2∠422BD6 cm2 4.如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ; AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .5、在ΔABC中,CD是中线,已知
BC-AC=5cm,ΔDBC的周长为25cm,
求ΔADC的周长. 1. 如图:AD,AE分别是△ABC的高和中线,且AB=8㎝ ,AC=6㎝,BC=10 cm,∠CAB=90°.试求:(1)AD的长;
(2)△ABE的面积;
(3)△ABE和△ACE的周长差.
(3) ∵ C△AEC =AC+CE+AE
C△ABE =AB+BE+AE ,
∴ C△AEC-C△ABE=AC+CE+AE-(AB+BE+AE)
=AC-AB=8-6=2 cm.
感悟与反思通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
有什么需要同学们帮助解决的问题吗?从知识上,在小学学习的基础上,我们又学习了什么?从方法上,我们是怎么认识这些重要线段的。对你后续的学习有什么启示吗?作业:P49 A 3 B 6
同课章节目录
