22.1比例线段4课件
图片预览

文档简介
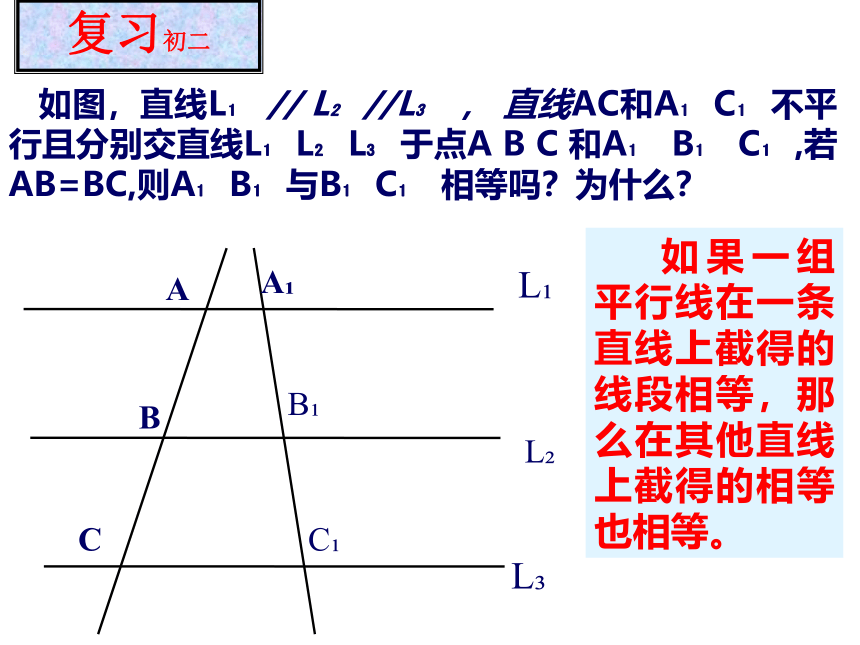
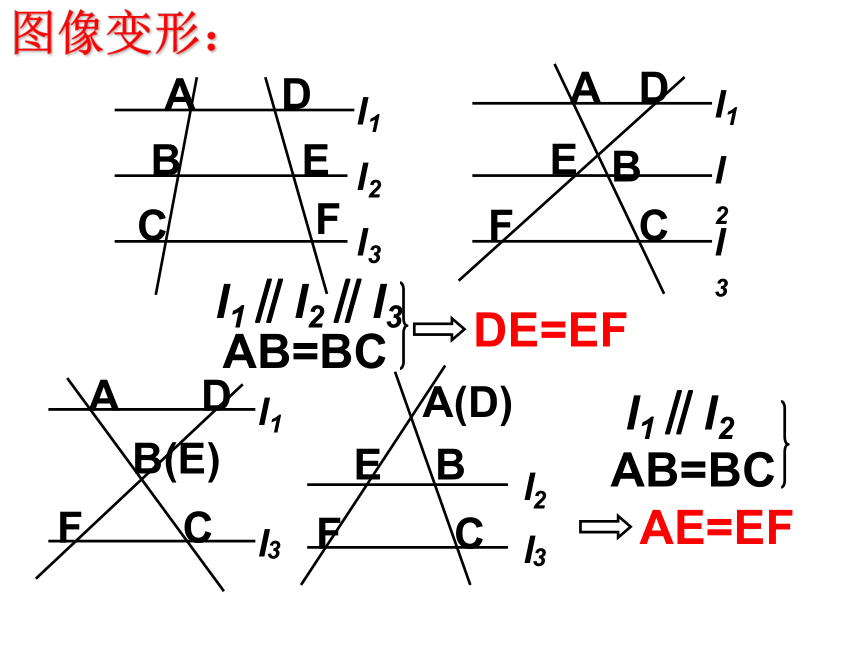
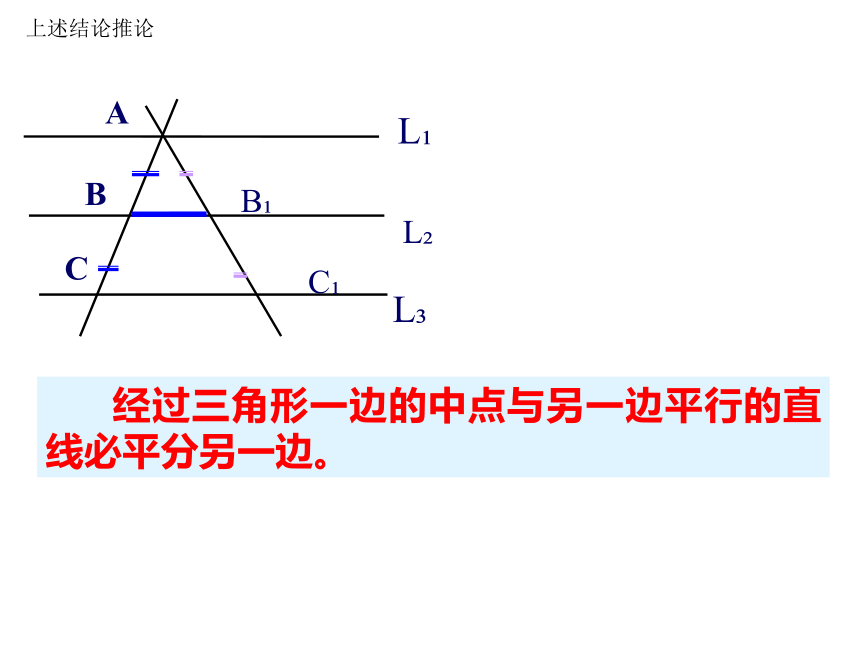
课件17张PPT。平行线分线段成比例定理 如图,直线L? // L?//L? , 直线AC和A?C?不平行且分别交直线L?L?L?于点A B C 和A? B? C?,若AB=BC,则A?B?与B?C? 相等吗?为什么?复习初二 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的相等也相等。图像变形:上述结论推论L?L?CB?ABL?C? 经过三角形一边的中点与另一边平行的直线必平分另一边。如果再取AD中点G,过点G作GH//DE交AC于点H,GH·由平行线等分线段定理可知:∴AG=GD: 上面的例子告诉我们,在三角形
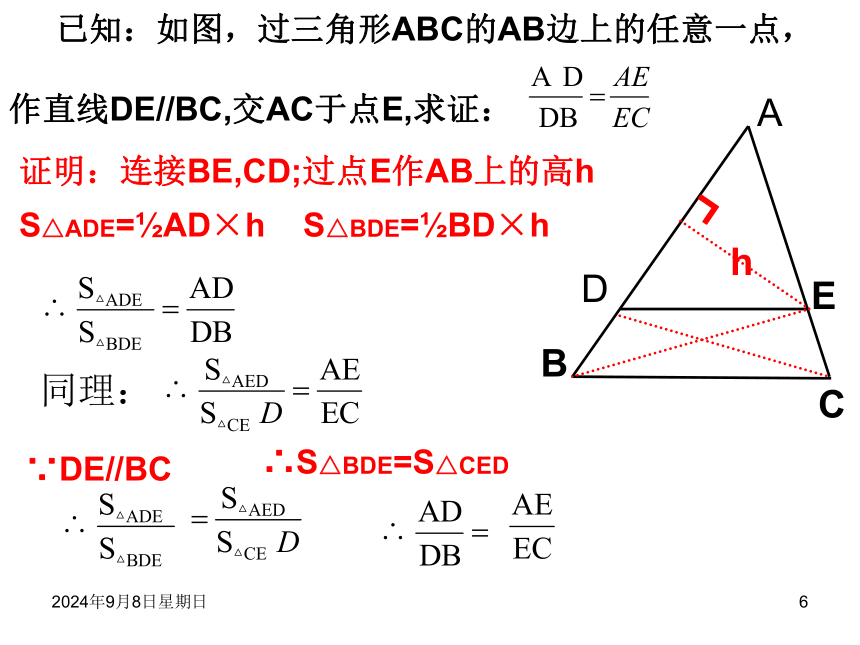
ABC的AB边上取特殊点G 、D,
过它们作直线平行于BC,并分别
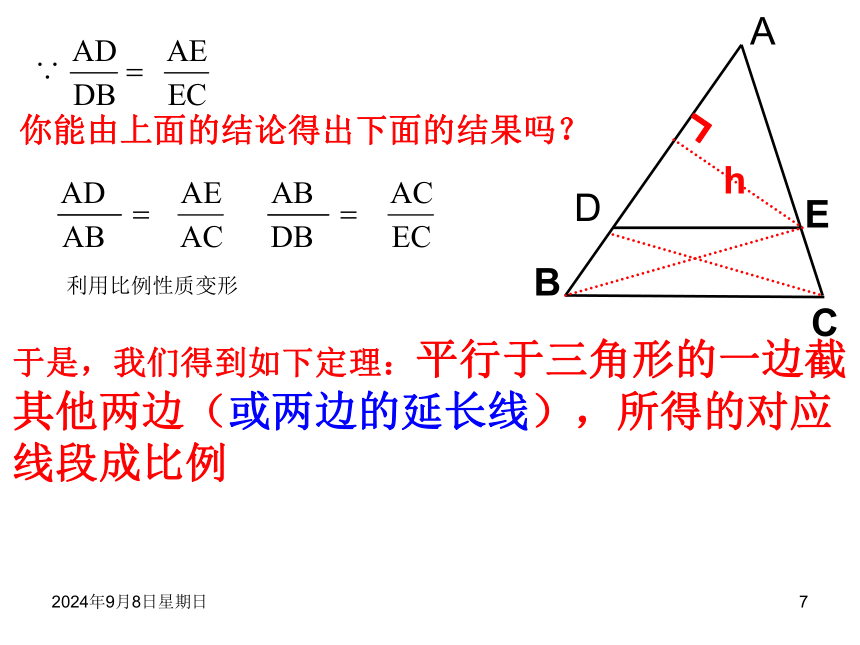
交AC与点H、E时,则有: 于是,我们猜想:当D点为AB上的任意一点,上述性质是否成立呢?证明:连接BE,CD;过点E作AB上的高hh┓S△ADE=?AD×hS△BDE=?BD×h同理:∵DE//BC∴S△BDE=S△CED2018年10月26日星期五1你能由上面的结论得出下面的结果吗?利用比例性质变形于是,我们得到如下定理:平行于三角形的一边截其他两边(或两边的延长线),所得的对应线段成比例2018年10月26日星期五1图形变形:2018年10月26日星期五1证明:过A作DF的平行线,分别交L?、L?于E′、F′ 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,求证:E′F′这时有而四边形AE′ED和四边形E′F′FE都是平行四边形所以 AE′=DE,E′F′=EF平行线分线段成比例定理:两条直线被三条平行线所截,截得的对应线段成比例2018年10月26日星期五1证明:过A作DF的平行线,分别交L?、L?于E′、F′ 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,求证:L?E′F′这时有而四边形AE′ED和四边形E′F′FE都是平行四边形所以 AE′=DE,E′F′=EF2018年10月26日星期五1 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,求证:E′F′E′F′平行线分线段成比例定理:两条直线被三条平行线所截,截得的对应线段成比例2018年10月26日星期五1 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,则:E′F′E′F′平行线等分线段成比例定理:两条直线被三条平行线所截,如果在其中一条直线上线段相等,那么在另一条直线上截得的线段也线段。若则即:当AB=BC时,有DE=EF2018年10月26日星期五1若两条直线被一组平行线所截,有该如何呢?有一组平行线:L1//L2/L3//....LK//..LN-1//LN根据已学定理,如果A1A2=A2A3=...AN-1AN1另外,直线A1AN与直线B1BN被这一组平行直线分别截于点A1,A2,A3...AK...AN-1,AN和B1,B2,B3...BK...BN-1,BN那么,B1B2=B2B3=...BN-1BN1这时,如果设A1A2=A2A3=...AN-1AN=aB1B2=B2B3=...BN-1BN=b平行线等分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。例1. (1)如图: l1∥l2∥l3 , ∴BC=6(1)若AB=3 , DE=2, EF=4,求BC.2018年10月26日星期五1例1. (1)如图: l1∥l2∥l3 , (2)若AC=8,DE=2,EF=3,求AB.∴AB=3.22018年10月26日星期五1同学们再见!同学们再见!
ABC的AB边上取特殊点G 、D,
过它们作直线平行于BC,并分别
交AC与点H、E时,则有: 于是,我们猜想:当D点为AB上的任意一点,上述性质是否成立呢?证明:连接BE,CD;过点E作AB上的高hh┓S△ADE=?AD×hS△BDE=?BD×h同理:∵DE//BC∴S△BDE=S△CED2018年10月26日星期五1你能由上面的结论得出下面的结果吗?利用比例性质变形于是,我们得到如下定理:平行于三角形的一边截其他两边(或两边的延长线),所得的对应线段成比例2018年10月26日星期五1图形变形:2018年10月26日星期五1证明:过A作DF的平行线,分别交L?、L?于E′、F′ 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,求证:E′F′这时有而四边形AE′ED和四边形E′F′FE都是平行四边形所以 AE′=DE,E′F′=EF平行线分线段成比例定理:两条直线被三条平行线所截,截得的对应线段成比例2018年10月26日星期五1证明:过A作DF的平行线,分别交L?、L?于E′、F′ 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,求证:L?E′F′这时有而四边形AE′ED和四边形E′F′FE都是平行四边形所以 AE′=DE,E′F′=EF2018年10月26日星期五1 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,求证:E′F′E′F′平行线分线段成比例定理:两条直线被三条平行线所截,截得的对应线段成比例2018年10月26日星期五1 已知:如图直线L?//L?//L?,直线AC、DF被这三条平行线分别截于点A、B、C和D、E、F,则:E′F′E′F′平行线等分线段成比例定理:两条直线被三条平行线所截,如果在其中一条直线上线段相等,那么在另一条直线上截得的线段也线段。若则即:当AB=BC时,有DE=EF2018年10月26日星期五1若两条直线被一组平行线所截,有该如何呢?有一组平行线:L1//L2/L3//....LK//..LN-1//LN根据已学定理,如果A1A2=A2A3=...AN-1AN1另外,直线A1AN与直线B1BN被这一组平行直线分别截于点A1,A2,A3...AK...AN-1,AN和B1,B2,B3...BK...BN-1,BN那么,B1B2=B2B3=...BN-1BN1这时,如果设A1A2=A2A3=...AN-1AN=aB1B2=B2B3=...BN-1BN=b平行线等分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。例1. (1)如图: l1∥l2∥l3 , ∴BC=6(1)若AB=3 , DE=2, EF=4,求BC.2018年10月26日星期五1例1. (1)如图: l1∥l2∥l3 , (2)若AC=8,DE=2,EF=3,求AB.∴AB=3.22018年10月26日星期五1同学们再见!同学们再见!
