22.2 相似三角形的判定课件
图片预览




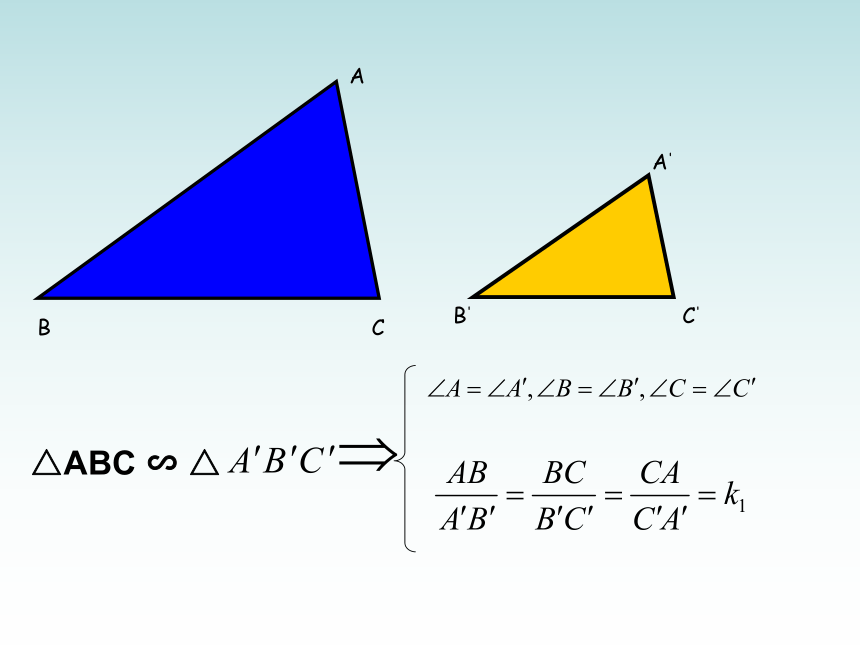
文档简介
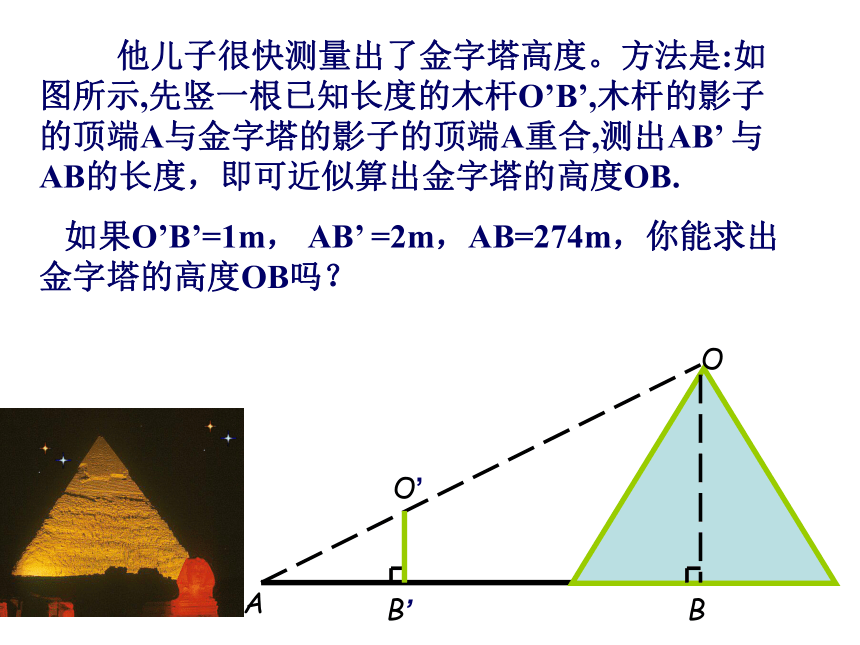
课件21张PPT。相似三角形的判定 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 走近金字塔 埃及著名的考古专家穆罕穆德,在一个烈日高照的上午.和儿子小穆罕穆德来到了金字塔脚下,他要他14岁的儿子用一根1米高的木杆,一把皮尺测出胡夫金字塔的高度.1米木杆皮尺 他儿子很快测量出了金字塔高度。方法是:如图所示,先竖一根已知长度的木杆O’B’,木杆的影子的顶端A与金字塔的影子的顶端A重合,测出AB’ 与AB的长度,即可近似算出金字塔的高度OB.
如果O’B’=1m, AB’ =2m,AB=274m,你能求出金字塔的高度OB吗?两个三角形应具有哪些条件才是相似的呢?你能给相似三角形下个定义吗? 三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形
△ ABC与△ DEF相似,就记作:
△ ABC∽ △DEF
注意:要把表示对应顶点的字母写在对应的位置上!
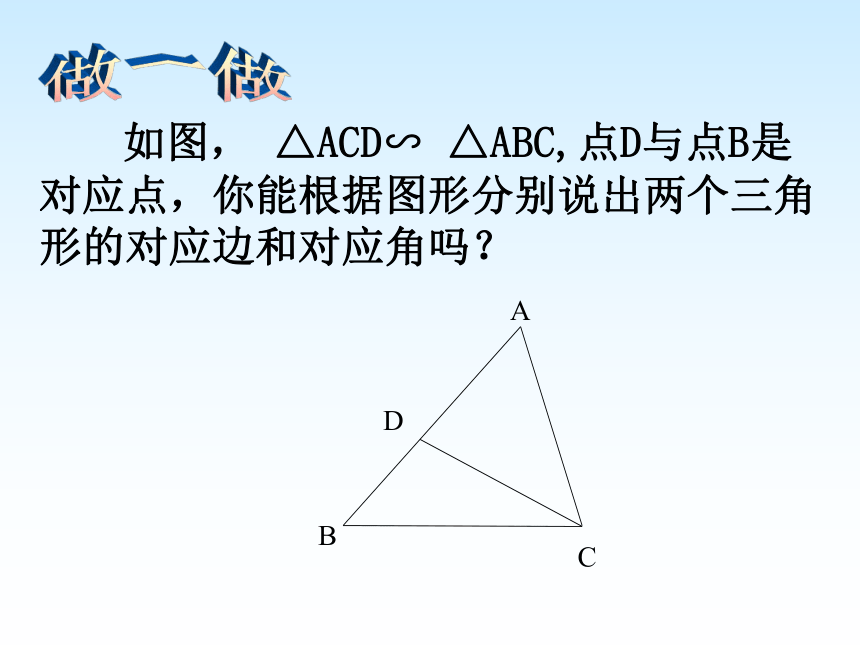
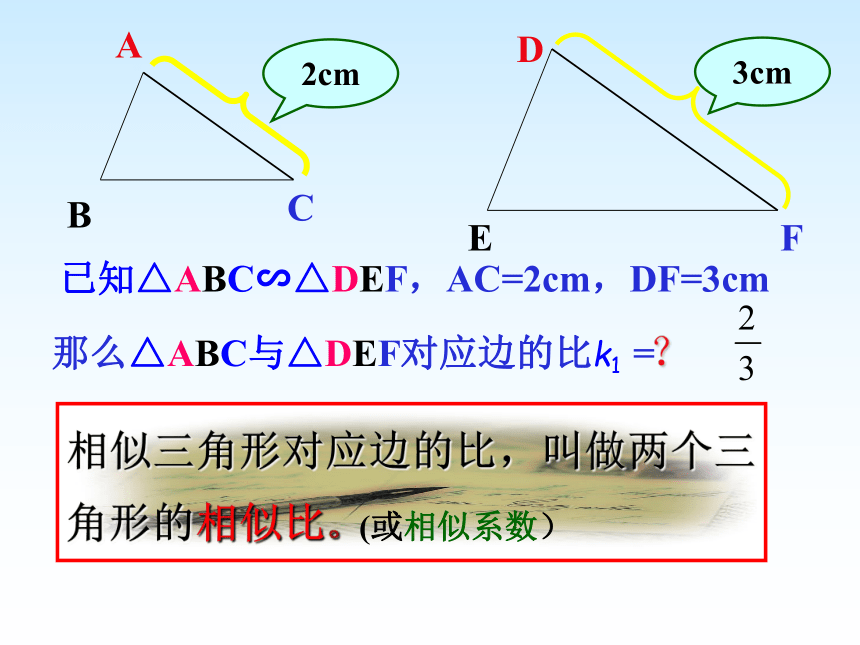
如图, △ACD∽ △ABC,点D与点B是对应点,你能根据图形分别说出两个三角形的对应边和对应角吗?做一做ABCDEF2cm3cm那么△ABC与△DEF对应边的比k1 =已知△ABC∽△DEF,AC=2cm,DF=3cm相似三角形对应边的比,叫做两个三角形的相似比。(或相似系数)?ABCDEF2cm3cm那么△ABC与△DEF对应边的比k1 =已知△ABC∽△DEF,AC=2cm,DF=3cm△DEF与△ABC对应边的比k2=
三角形的前后次序不同,所得相似比不同。K1与k2之间是什么关系?ABC在什么条件下有K1=k2呢?B'C'A'两个全等三角形一定相似,全等是相似的一种特例。原来我们学习过全等三角形的定义可以用来判定两个三角形是否全等,那相似三角形的定义有什么用?作用:
可以利用定义来判定两个三角形相似,反过来,如果两个三角形相似,有对应角相等,对应边成比例的性质。动脑筋,想一想1、如图,在△ABC中,点D是边AB的中点,DE∥BC,DE交AC于点E ,△ADE与△ABC有什么关系?ABCDE我们通过相似的定义证明这个结论.活动2直觉告诉我们,△ADE与△ABC相似.这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似,相似比为先证明两个三角形的对应角相等.在△ADE与△ABC中,∠A=∠A∵DE∥BC∴∠ADE=∠B,∠AED=∠C再证明两个三角形的对应边的比相等.过点E作EF∥AB,EF交BC于点F.在 BFED中,DE=BF,DB=EF∵AD=BD= AB∴AD=EF又∠A=∠1,∠2=∠C∴△ADE≌△EFC∴AE=EC= ACDE=FC=BF= BCABCDEF122、如果点D1、D2是边AB的三等分点, D1E1 、D2E2都与BC平行,此时△AD1E1、 △AD2E2与△ABC是否还相似呢?ABCD1E1F1D2F2E2猜测:如果点D为边AB的任意一点, △ADE与△ABC也相似吗?定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.∵ DE∥BC∴△ADE∽△ABC1、由DE∥BC你还能得出哪些比例式?2、如果 ,AC=8cm,求AE的长。小试牛刀3.如图,点D在△ABC的边AB的反向延长线上,DE∥BC,交AC的延长线于点E,写出所有可能的比例式。小试牛刀 如果O’B’=1m, AB’ =2m,AB=274m,你能求出金字塔的高度OB吗?小结1、内容总结 本节课你学到了哪些知识?2、方法归纳 在本节课的探索过程中,哪些方法你觉得较好?从一般到特殊、从特殊到一般、类比、转化相似三角形定义:对应角相等,对应边成比例
表示法: △ABC∽△A′B′C′
相似比:对应边的比三角形相似判定定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
如果O’B’=1m, AB’ =2m,AB=274m,你能求出金字塔的高度OB吗?两个三角形应具有哪些条件才是相似的呢?你能给相似三角形下个定义吗? 三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形
△ ABC与△ DEF相似,就记作:
△ ABC∽ △DEF
注意:要把表示对应顶点的字母写在对应的位置上!
如图, △ACD∽ △ABC,点D与点B是对应点,你能根据图形分别说出两个三角形的对应边和对应角吗?做一做ABCDEF2cm3cm那么△ABC与△DEF对应边的比k1 =已知△ABC∽△DEF,AC=2cm,DF=3cm相似三角形对应边的比,叫做两个三角形的相似比。(或相似系数)?ABCDEF2cm3cm那么△ABC与△DEF对应边的比k1 =已知△ABC∽△DEF,AC=2cm,DF=3cm△DEF与△ABC对应边的比k2=
三角形的前后次序不同,所得相似比不同。K1与k2之间是什么关系?ABC在什么条件下有K1=k2呢?B'C'A'两个全等三角形一定相似,全等是相似的一种特例。原来我们学习过全等三角形的定义可以用来判定两个三角形是否全等,那相似三角形的定义有什么用?作用:
可以利用定义来判定两个三角形相似,反过来,如果两个三角形相似,有对应角相等,对应边成比例的性质。动脑筋,想一想1、如图,在△ABC中,点D是边AB的中点,DE∥BC,DE交AC于点E ,△ADE与△ABC有什么关系?ABCDE我们通过相似的定义证明这个结论.活动2直觉告诉我们,△ADE与△ABC相似.这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似,相似比为先证明两个三角形的对应角相等.在△ADE与△ABC中,∠A=∠A∵DE∥BC∴∠ADE=∠B,∠AED=∠C再证明两个三角形的对应边的比相等.过点E作EF∥AB,EF交BC于点F.在 BFED中,DE=BF,DB=EF∵AD=BD= AB∴AD=EF又∠A=∠1,∠2=∠C∴△ADE≌△EFC∴AE=EC= ACDE=FC=BF= BCABCDEF122、如果点D1、D2是边AB的三等分点, D1E1 、D2E2都与BC平行,此时△AD1E1、 △AD2E2与△ABC是否还相似呢?ABCD1E1F1D2F2E2猜测:如果点D为边AB的任意一点, △ADE与△ABC也相似吗?定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.∵ DE∥BC∴△ADE∽△ABC1、由DE∥BC你还能得出哪些比例式?2、如果 ,AC=8cm,求AE的长。小试牛刀3.如图,点D在△ABC的边AB的反向延长线上,DE∥BC,交AC的延长线于点E,写出所有可能的比例式。小试牛刀 如果O’B’=1m, AB’ =2m,AB=274m,你能求出金字塔的高度OB吗?小结1、内容总结 本节课你学到了哪些知识?2、方法归纳 在本节课的探索过程中,哪些方法你觉得较好?从一般到特殊、从特殊到一般、类比、转化相似三角形定义:对应角相等,对应边成比例
表示法: △ABC∽△A′B′C′
相似比:对应边的比三角形相似判定定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
