沪科版九数上22.2.6直角三角形相似判定课件
文档属性
| 名称 | 沪科版九数上22.2.6直角三角形相似判定课件 |  | |
| 格式 | zip | ||
| 文件大小 | 179.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-11 19:26:36 | ||
图片预览





文档简介
课件16张PPT。22.2.6直角三角形相似的判定ABCabcA′B′C′∟九(1)是我家,我爱我家!一、复习提问1、到目前为止我们总共学过几种判定两 个三
角形相似的方法?答:
(1)两角对应相等的两个三角形相似。
(2)两边对应成比例且夹角相等的两个三角形相似。
(3)三边对应成比例的两个三角形相似。
2、判定两个直角三角形相似有几种方法?答:一个锐角对应相等或两直角边对应成比例。课堂练习
填空:(填相似或不相似)
1、一个三角形有两个角分别是60°和35°,另一个三角形的两个角分别是60°和85°,那么这两个三角形 。
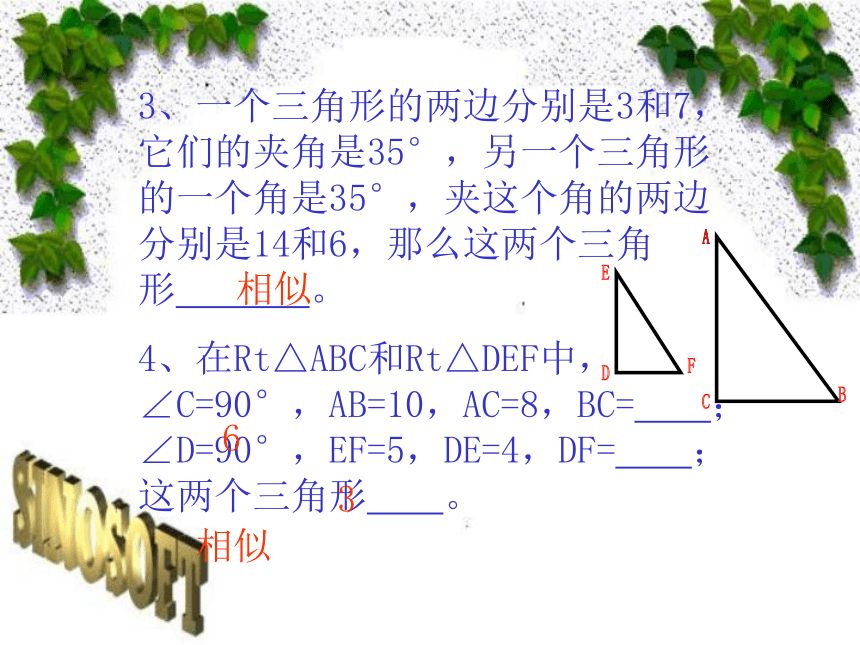
2、一个三角形的三边分别是3、4、5,另一个三角形的三边分别是6、8、10,那么这两个三角形 。相似相似3、一个三角形的两边分别是3和7,它们的夹角是35°,另一个三角形的一个角是35°,夹这个角的两边分别是14和6,那么这两个三角形 。
4、在Rt△ABC和Rt△DEF中,∠C=90°,AB=10,AC=8,BC= ;∠D=90°,EF=5,DE=4,DF= ;这两个三角形 。相似相似63BDEFACA返回上一张下一张4、在Rt△ABC和Rt△DEF中,∠C=90°,AB=10,AC=8,BC= ;∠D=90°,EF=5,DE=4,DF= ;这两个直角三角形 。
问题:1、这两个直角三角形的已知边(共四条)有什么关系?
2、你是如何证明这两个直角三角形相似的?相似 63二、学习内容
直角三角形相似判定定理;
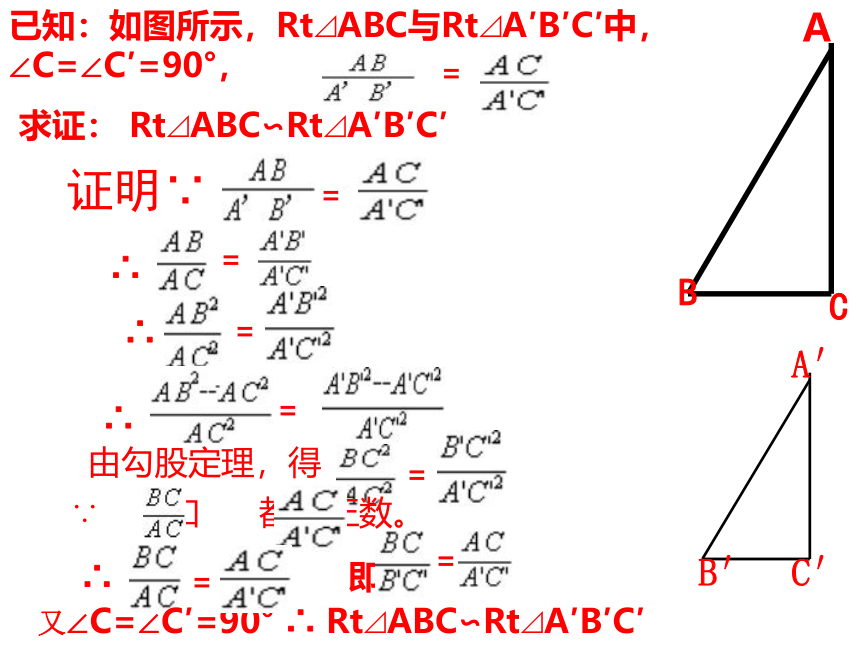
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。已知:如图所示,Rt⊿ABC与Rt⊿A′B′C′中,∠C=∠C′=90°,
求证: Rt⊿ABC∽Rt⊿A′B′C′BCA′B′C′A证明∵ =∴=∴==∴=由勾股定理,得=∵ 和 都是正数。∴ 即==又∠C=∠C′=90° ∴ Rt⊿ABC∽Rt⊿A′B′C′直角三角形相似的判定定理:
一直角边和斜边对应成比例的两个直角三角形相似。
练习一
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。依据下列各组条件判定这两个三角形是不是相似,并说明为什么。
1、∠A=25°,∠B′=65°。
2、AC=3,BC=4,A′C′=6,B′C′=8。
3、AB=10,AC=8,A′B′=15, B′C′=9。①解:∵∠A=25°, ∠C=90°。
∴ ∠B=65 °。
于是∠B′=65°=∠B ,
∠C′= 90°=∠C。
∴△ABC∽△A′B′C′。1、∠A=25°,∠B′=65°。②解:∵AC=3,BC=4,
A′C′=6,B′C′=8。
∴
∴
且∠C=∠C′=90°
∴ △ABC∽△A′B′C′
AC=3,BC=4,A′C′=6,B′C′=8。③解:∵AB=10,AC=8,∠C=90°。
∴BC=
∴
∴ 且∠C′=90°=∠C
∴ Rt△ABC∽Rt△A′B′C′3、AB=10,AC=8,A′B′=15, B′C′=9。练习二
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。要使Rt△ABC∽ Rt△A′B′C′,应加什么条件?
1、∠A=35° ,∠B′=________。
2、AC=5,BC=4,A′C′=15,B′C′=___。
3、AB=5,AC=___,A′B′=10, A′C′=6。
4、AB=10,BC=6, A′B′=5, A′C′=______.
5、AC:AB=1:3, A′C′=a, A′B′=_____ 55°12343a例:如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,⊿ABC∽ ⊿CDB?ABDCab分析:要使R t⊿ABC∽ R t⊿CDB
而题中已经知道R t⊿ABC的斜边和一直角边及R t⊿CDB的斜边,利用今天讲的这个定理可知只须加上条件 = 即可。解:∵ ∠ABC=∠CDB=90°
∴当 = 时, ⊿ABC∽ ⊿CDB。
即当 = 时, ⊿ABC∽ ⊿CDB
∴BD=
答:当BD= 时, ⊿ABC∽ ⊿CDB
问:若改为⊿ABC∽ ⊿BDC,结果如何?
CBD三、小结1、如何判定两个直角三角形相似呢?
答:一个锐角对应相等或两边对应成比例的两个直角三角形相似。
2、直角三角形相似的判定定理的简单应用。3、初步了解转移比例的证法。再见!作业:
1.课堂作业:P86 8,9,10题。
2.草稿纸作业:P84 练习
角形相似的方法?答:
(1)两角对应相等的两个三角形相似。
(2)两边对应成比例且夹角相等的两个三角形相似。
(3)三边对应成比例的两个三角形相似。
2、判定两个直角三角形相似有几种方法?答:一个锐角对应相等或两直角边对应成比例。课堂练习
填空:(填相似或不相似)
1、一个三角形有两个角分别是60°和35°,另一个三角形的两个角分别是60°和85°,那么这两个三角形 。
2、一个三角形的三边分别是3、4、5,另一个三角形的三边分别是6、8、10,那么这两个三角形 。相似相似3、一个三角形的两边分别是3和7,它们的夹角是35°,另一个三角形的一个角是35°,夹这个角的两边分别是14和6,那么这两个三角形 。
4、在Rt△ABC和Rt△DEF中,∠C=90°,AB=10,AC=8,BC= ;∠D=90°,EF=5,DE=4,DF= ;这两个三角形 。相似相似63BDEFACA返回上一张下一张4、在Rt△ABC和Rt△DEF中,∠C=90°,AB=10,AC=8,BC= ;∠D=90°,EF=5,DE=4,DF= ;这两个直角三角形 。
问题:1、这两个直角三角形的已知边(共四条)有什么关系?
2、你是如何证明这两个直角三角形相似的?相似 63二、学习内容
直角三角形相似判定定理;
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。已知:如图所示,Rt⊿ABC与Rt⊿A′B′C′中,∠C=∠C′=90°,
求证: Rt⊿ABC∽Rt⊿A′B′C′BCA′B′C′A证明∵ =∴=∴==∴=由勾股定理,得=∵ 和 都是正数。∴ 即==又∠C=∠C′=90° ∴ Rt⊿ABC∽Rt⊿A′B′C′直角三角形相似的判定定理:
一直角边和斜边对应成比例的两个直角三角形相似。
练习一
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。依据下列各组条件判定这两个三角形是不是相似,并说明为什么。
1、∠A=25°,∠B′=65°。
2、AC=3,BC=4,A′C′=6,B′C′=8。
3、AB=10,AC=8,A′B′=15, B′C′=9。①解:∵∠A=25°, ∠C=90°。
∴ ∠B=65 °。
于是∠B′=65°=∠B ,
∠C′= 90°=∠C。
∴△ABC∽△A′B′C′。1、∠A=25°,∠B′=65°。②解:∵AC=3,BC=4,
A′C′=6,B′C′=8。
∴
∴
且∠C=∠C′=90°
∴ △ABC∽△A′B′C′
AC=3,BC=4,A′C′=6,B′C′=8。③解:∵AB=10,AC=8,∠C=90°。
∴BC=
∴
∴ 且∠C′=90°=∠C
∴ Rt△ABC∽Rt△A′B′C′3、AB=10,AC=8,A′B′=15, B′C′=9。练习二
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。要使Rt△ABC∽ Rt△A′B′C′,应加什么条件?
1、∠A=35° ,∠B′=________。
2、AC=5,BC=4,A′C′=15,B′C′=___。
3、AB=5,AC=___,A′B′=10, A′C′=6。
4、AB=10,BC=6, A′B′=5, A′C′=______.
5、AC:AB=1:3, A′C′=a, A′B′=_____ 55°12343a例:如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,⊿ABC∽ ⊿CDB?ABDCab分析:要使R t⊿ABC∽ R t⊿CDB
而题中已经知道R t⊿ABC的斜边和一直角边及R t⊿CDB的斜边,利用今天讲的这个定理可知只须加上条件 = 即可。解:∵ ∠ABC=∠CDB=90°
∴当 = 时, ⊿ABC∽ ⊿CDB。
即当 = 时, ⊿ABC∽ ⊿CDB
∴BD=
答:当BD= 时, ⊿ABC∽ ⊿CDB
问:若改为⊿ABC∽ ⊿BDC,结果如何?
CBD三、小结1、如何判定两个直角三角形相似呢?
答:一个锐角对应相等或两边对应成比例的两个直角三角形相似。
2、直角三角形相似的判定定理的简单应用。3、初步了解转移比例的证法。再见!作业:
1.课堂作业:P86 8,9,10题。
2.草稿纸作业:P84 练习
