22.2相似三角形2课件
图片预览


文档简介
课件13张PPT。相似三角形2复习:
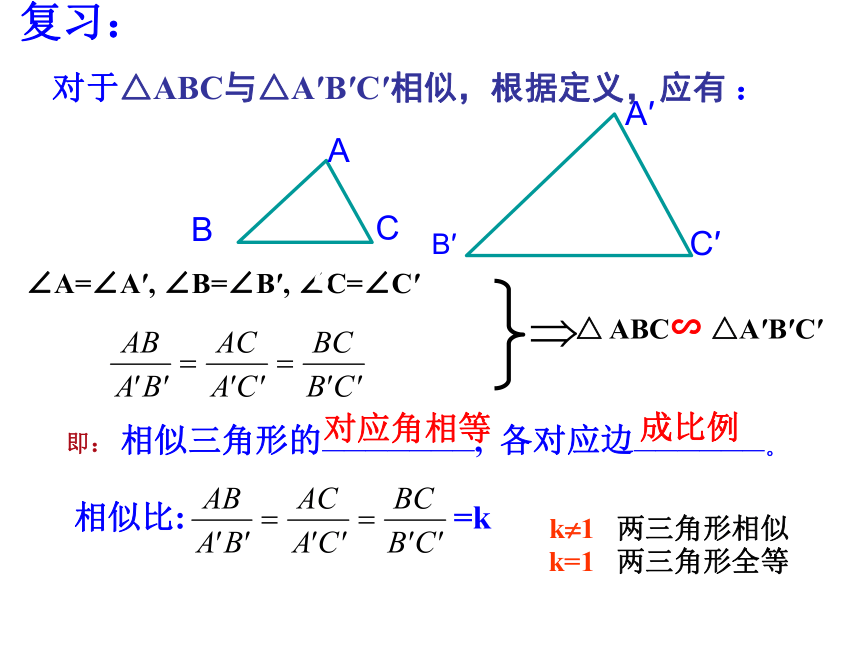
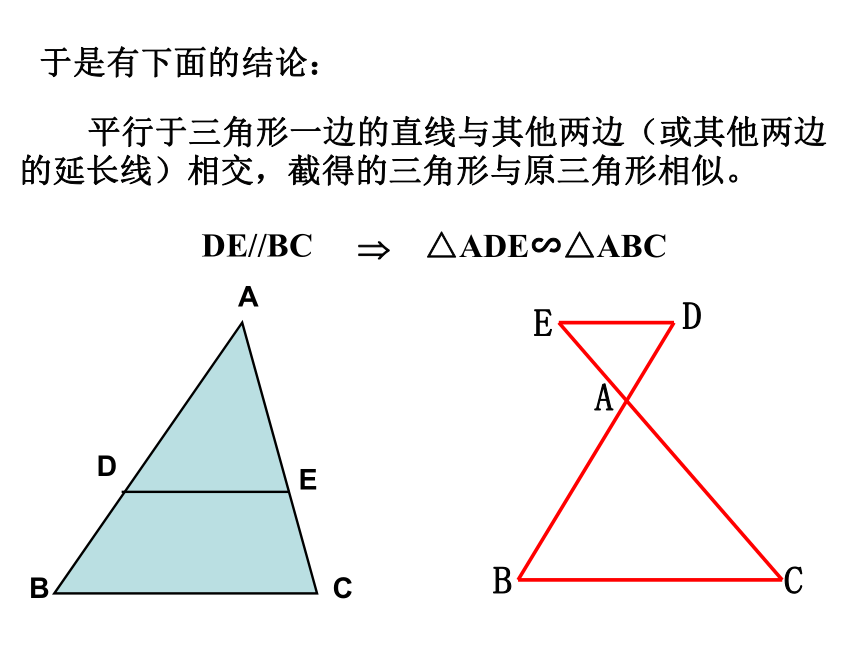
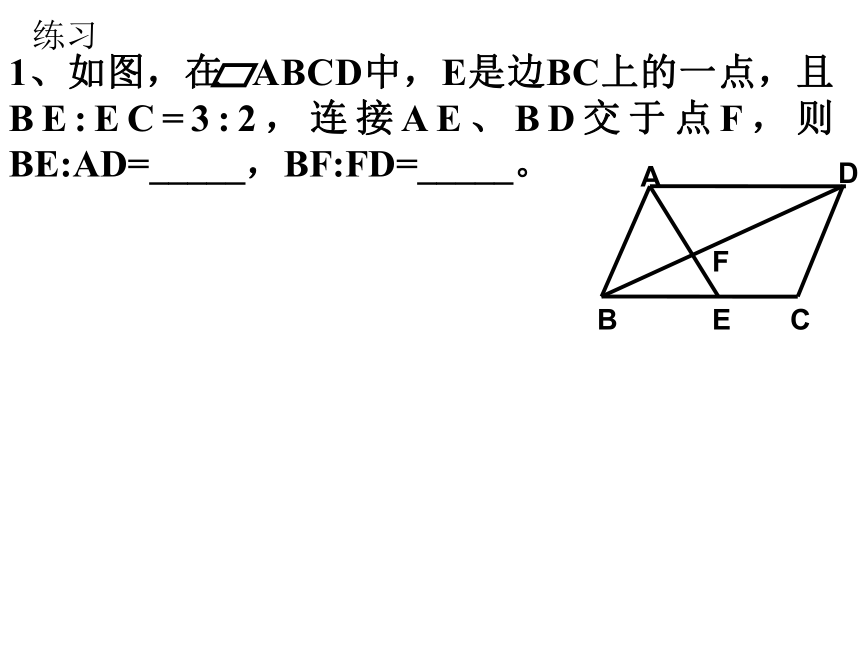
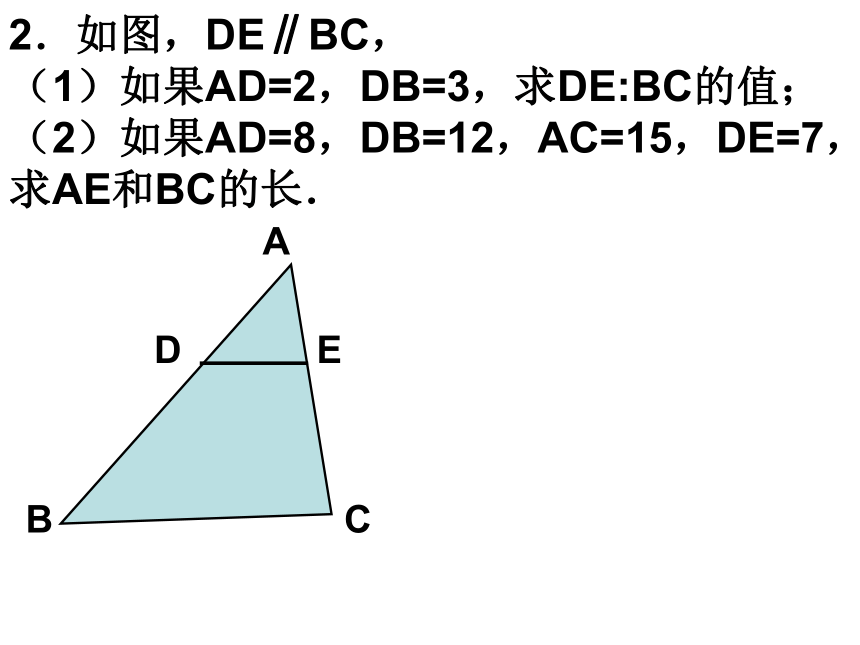
对于△ABC与△A′B′C′相似,根据定义,应有 :即: 相似三角形的———————, 各对应边——————。对应角相等成比例∠A=∠A′, ∠B=∠B′, ∠C=∠C′△ ABC∽ △A′B′C′k?1 两三角形相似 k=1 两三角形全等 相似比: =k 当且仅当两个三角形全等时,才有k?=k?;所以全等三角形是相似三角形的特例。这里的结论,对于任意两个相似多边形都成立可得:将△ ABC与 △A′B′C′的相似比记做为k?则△A′B′C′与△ ABC的相似比记做为k?于是有下面的结论: 平行于三角形一边的直线与其他两边(或其他两边的延长线)相交,截得的三角形与原三角形相似。练习2.如图,DE∥BC,
(1)如果AD=2,DB=3,求DE:BC的值;
(2)如果AD=8,DB=12,AC=15,DE=7,求AE和BC的长.3.如图,在□ABCD中,EF∥AB,DE:EA=2:3,EF=4,求CD的长. 4.已知EF∥BC,求证:5.已知EF∥BC,求证:6、如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=______。7、已知:DE//BC,DF//AC,若 BF=3,CF=2,DF=6,你能求出线段AE的长度吗?∴△BDF∽△BAC∵DF∥AC∴∴解:∵DE∥BC,DF∥AC∴四边形DFCE为平行四边形∴FC=DE=2,EC=DF=6∴AE=AC-CE=10-6=4∴△BDM∽△BAC解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB同学们再见
对于△ABC与△A′B′C′相似,根据定义,应有 :即: 相似三角形的———————, 各对应边——————。对应角相等成比例∠A=∠A′, ∠B=∠B′, ∠C=∠C′△ ABC∽ △A′B′C′k?1 两三角形相似 k=1 两三角形全等 相似比: =k 当且仅当两个三角形全等时,才有k?=k?;所以全等三角形是相似三角形的特例。这里的结论,对于任意两个相似多边形都成立可得:将△ ABC与 △A′B′C′的相似比记做为k?则△A′B′C′与△ ABC的相似比记做为k?于是有下面的结论: 平行于三角形一边的直线与其他两边(或其他两边的延长线)相交,截得的三角形与原三角形相似。练习2.如图,DE∥BC,
(1)如果AD=2,DB=3,求DE:BC的值;
(2)如果AD=8,DB=12,AC=15,DE=7,求AE和BC的长.3.如图,在□ABCD中,EF∥AB,DE:EA=2:3,EF=4,求CD的长. 4.已知EF∥BC,求证:5.已知EF∥BC,求证:6、如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=______。7、已知:DE//BC,DF//AC,若 BF=3,CF=2,DF=6,你能求出线段AE的长度吗?∴△BDF∽△BAC∵DF∥AC∴∴解:∵DE∥BC,DF∥AC∴四边形DFCE为平行四边形∴FC=DE=2,EC=DF=6∴AE=AC-CE=10-6=4∴△BDM∽△BAC解:∵MD∥AC,又∵ ME∥AB,∴△CEM∽△CAB同学们再见
