22.2直角三角形相似的判定导学案(无答案)
文档属性
| 名称 | 22.2直角三角形相似的判定导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 12.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-11 00:00:00 | ||
图片预览

文档简介
直角三角形相似的判定导学案
导学目标:
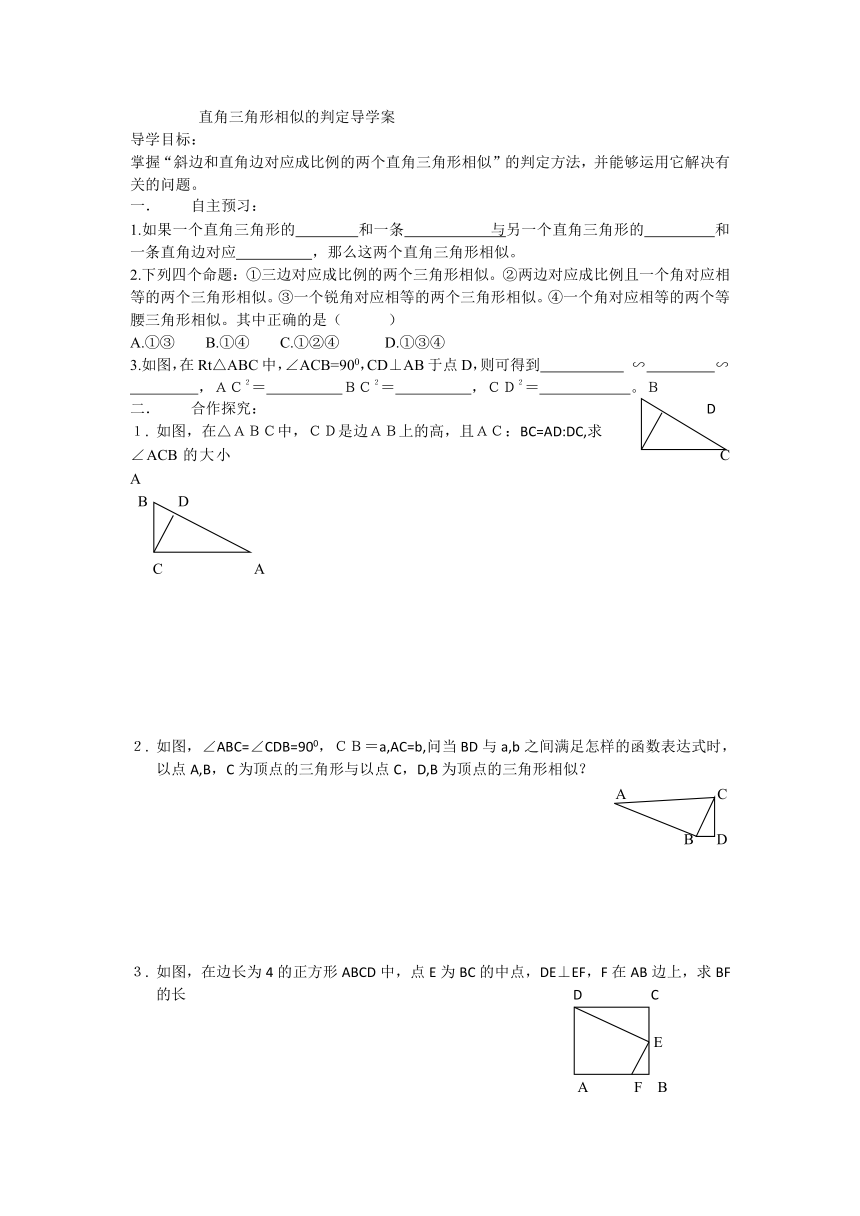
掌握“斜边和直角边对应成比例的两个直角三角形相似”的判定方法,并能够运用它解决有关的问题。
自主预习:
1.如果一个直角三角形的 和一条 与另一个直角三角形的 和 一条直角边对应 ,那么这两个直角三角形相似。
2.下列四个命题:①三边对应成比例的两个三角形相似。②两边对应成比例且一个角对应相等的两个三角形相似。③一个锐角对应相等的两个三角形相似。④一个角对应相等的两个等腰三角形相似。其中正确的是( )
A.①③ B.①④ C.①②④ D.①③④
3.如图,在Rt△ABC中,∠ACB=900,CD⊥AB于点D,则可得到 ∽ ∽
,AC2= BC2= ,CD2= 。B
合作探究: D
如图,在△ABC中,CD是边AB上的高,且AC:BC=AD:DC,求
∠ACB的大小 C A
B D
C A
如图,∠ABC=∠CDB=900,CB=a,AC=b,问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似?
A C
B D
如图,在边长为4的正方形ABCD中,点E为BC的中点,DE⊥EF,F在AB边上,求BF的长 D C
E
A F B
展评提升:
1.如图,在△ABC中,AD⊥BC于D,P是AD上任意一点,PE⊥AB于E,PF⊥AC于F,求证:AE●AB=AF●AC A
E
P F
B D C
2.如图,已知∠ACB=900,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F
①求证:△CEB≌△ADC ② 若AD=9cm,DE=6cm,求BE及EF的长
B E
F
D D
C A
自我检测:
依据下列条件,判断△ABC与△A1B1C1是否相似,并说明理由
∠C=∠C1=900,∠A=750,∠B1=150
②∠C=900,AC=3,BC=4,∠C1=900,A1C1=5,B1C1=12
C=900,AB=13 ,BC=5,∠C1=900,A1B1=26,A1C1=24
2.△ABC的三边长分别是3,4,5.与其相似的△DEF的最大边长为15 ,那么S△DEF=
3.课本练习P84.第1,2,3,4,题
五.课堂小结:
1判定三角形相似有哪些方法?
2.通过本节课学习,你有哪些收获,还有什么疑惑?请与同学交流!
导学目标:
掌握“斜边和直角边对应成比例的两个直角三角形相似”的判定方法,并能够运用它解决有关的问题。
自主预习:
1.如果一个直角三角形的 和一条 与另一个直角三角形的 和 一条直角边对应 ,那么这两个直角三角形相似。
2.下列四个命题:①三边对应成比例的两个三角形相似。②两边对应成比例且一个角对应相等的两个三角形相似。③一个锐角对应相等的两个三角形相似。④一个角对应相等的两个等腰三角形相似。其中正确的是( )
A.①③ B.①④ C.①②④ D.①③④
3.如图,在Rt△ABC中,∠ACB=900,CD⊥AB于点D,则可得到 ∽ ∽
,AC2= BC2= ,CD2= 。B
合作探究: D
如图,在△ABC中,CD是边AB上的高,且AC:BC=AD:DC,求
∠ACB的大小 C A
B D
C A
如图,∠ABC=∠CDB=900,CB=a,AC=b,问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似?
A C
B D
如图,在边长为4的正方形ABCD中,点E为BC的中点,DE⊥EF,F在AB边上,求BF的长 D C
E
A F B
展评提升:
1.如图,在△ABC中,AD⊥BC于D,P是AD上任意一点,PE⊥AB于E,PF⊥AC于F,求证:AE●AB=AF●AC A
E
P F
B D C
2.如图,已知∠ACB=900,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F
①求证:△CEB≌△ADC ② 若AD=9cm,DE=6cm,求BE及EF的长
B E
F
D D
C A
自我检测:
依据下列条件,判断△ABC与△A1B1C1是否相似,并说明理由
∠C=∠C1=900,∠A=750,∠B1=150
②∠C=900,AC=3,BC=4,∠C1=900,A1C1=5,B1C1=12
C=900,AB=13 ,BC=5,∠C1=900,A1B1=26,A1C1=24
2.△ABC的三边长分别是3,4,5.与其相似的△DEF的最大边长为15 ,那么S△DEF=
3.课本练习P84.第1,2,3,4,题
五.课堂小结:
1判定三角形相似有哪些方法?
2.通过本节课学习,你有哪些收获,还有什么疑惑?请与同学交流!
