人教版数学九年级上册22.1二次函数图象与性质复习课件
文档属性
| 名称 | 人教版数学九年级上册22.1二次函数图象与性质复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 601.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-11 20:50:35 | ||
图片预览





文档简介
课件14张PPT。二次函数的图象与性质复习课
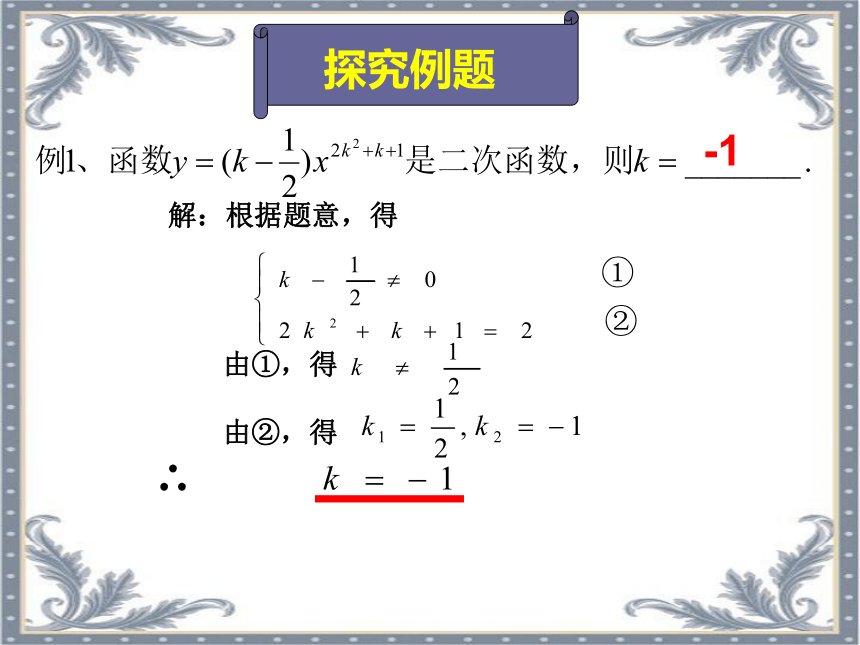
二次函数定义注意:1. 自变量的最高次数是2。2. 二次项的系数a≠0。3. 二次函数解析式必须是整式。①②由①,得由②,得∴解:根据题意,得-1探究例题1、下列函数中,是二次函数的是 .
① ② ③
④ ⑤ ⑥
⑦ ⑧
2.当m_______时,函数y=(m+1)χ - 2χ+1
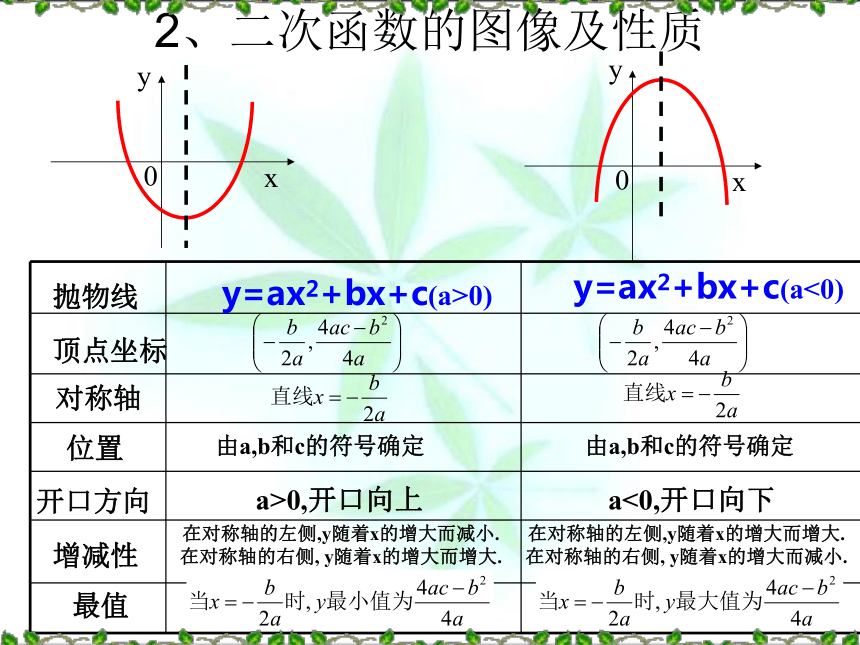
是二次函数?① ② ③ ⑦=2随堂练习2、二次函数的图像及性质 抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定a>0,开口向上a<0,开口向下在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 例2:
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
(3)x为何值时,y随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。例2:已知二次函数解:
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
例2:已知二次函数0xx=-1???(-3,0)(1,0)?解解0xx=-1??(0,-–)??(-3,0)(1,0)3 2:(3)?(-1,-2)当x=-1时,y有最小值为
y最小值=-2
当x<-1时,y随x的增大
而减少;
(3)x为何值时,y 随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
例2:已知二次函数解:0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx由图象可知(4) 当x< -3或x>1时,y > 0当-3 < x < 1时,y < 0
(4)x为何值时,y<0?x为何值时,y>0?
例2:已知二次函数4、3、抛物线 的对称轴及顶点坐标分别是( )
A、y轴,(0,-4) B、x=3,(0,4)
C、x轴,(0,0) D、y轴, (0,3)
D二次函数 的最值为( )
A、最大值1 B、最小值1
C、最大值2 D、最小值2D5、二次函数y=ax2+bx+c,当a>0时,在对称轴右侧,y随x的增大而 ,在对称轴左侧,y随x的增大而 ;当a<0时,在对称轴右侧,y随x的增大而 , 在对称轴左侧,y随x的增大而 。增大减小减小增大0????xy小结反思: 1、二次函数的概念
2、二次函数的图象及性质
作业:祝愿智慧花结出
丰硕果!
二次函数定义注意:1. 自变量的最高次数是2。2. 二次项的系数a≠0。3. 二次函数解析式必须是整式。①②由①,得由②,得∴解:根据题意,得-1探究例题1、下列函数中,是二次函数的是 .
① ② ③
④ ⑤ ⑥
⑦ ⑧
2.当m_______时,函数y=(m+1)χ - 2χ+1
是二次函数?① ② ③ ⑦=2随堂练习2、二次函数的图像及性质 抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定a>0,开口向上a<0,开口向下在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 例2:
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
(3)x为何值时,y随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标。例2:已知二次函数解:
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
例2:已知二次函数0xx=-1???(-3,0)(1,0)?解解0xx=-1??(0,-–)??(-3,0)(1,0)3 2:(3)?(-1,-2)当x=-1时,y有最小值为
y最小值=-2
当x<-1时,y随x的增大
而减少;
(3)x为何值时,y 随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
例2:已知二次函数解:0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx由图象可知(4) 当x< -3或x>1时,y > 0当-3 < x < 1时,y < 0
(4)x为何值时,y<0?x为何值时,y>0?
例2:已知二次函数4、3、抛物线 的对称轴及顶点坐标分别是( )
A、y轴,(0,-4) B、x=3,(0,4)
C、x轴,(0,0) D、y轴, (0,3)
D二次函数 的最值为( )
A、最大值1 B、最小值1
C、最大值2 D、最小值2D5、二次函数y=ax2+bx+c,当a>0时,在对称轴右侧,y随x的增大而 ,在对称轴左侧,y随x的增大而 ;当a<0时,在对称轴右侧,y随x的增大而 , 在对称轴左侧,y随x的增大而 。增大减小减小增大0????xy小结反思: 1、二次函数的概念
2、二次函数的图象及性质
作业:祝愿智慧花结出
丰硕果!
同课章节目录
