人教版数学九年级上册第22章《二次函数》复习课件
文档属性
| 名称 | 人教版数学九年级上册第22章《二次函数》复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-11 00:00:00 | ||
图片预览



文档简介
课件12张PPT。聪谜语专题复习
教材典型题拓展
(孙悟空七十二变)1、立足于新理念 抓学习习惯
2、立足于新课标 抓能力培养
3、立足于课堂 抓复习效率
4、立足于教材 抓习题变换
5、立足于反思 抓解题本质
6、立足于数学思想 抓综合运用
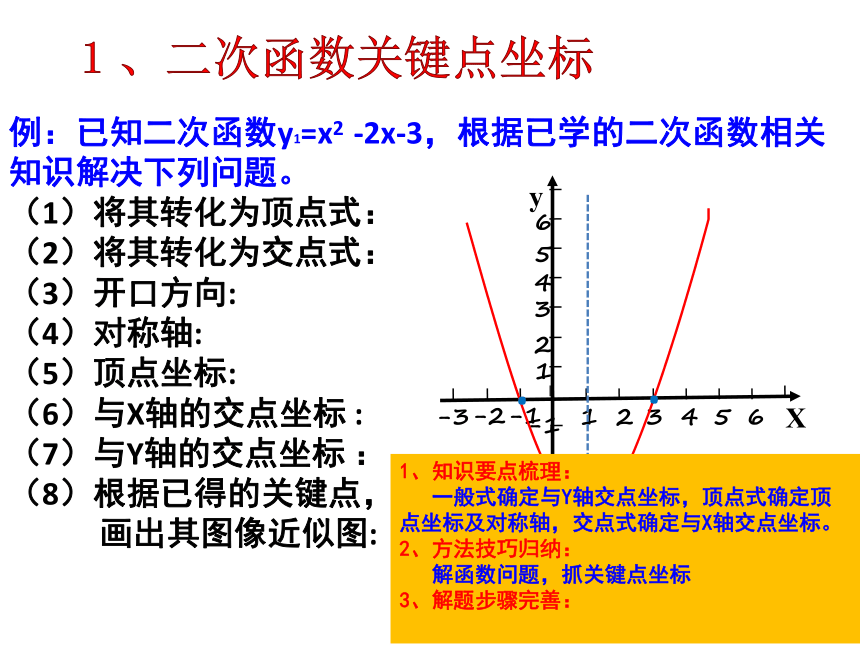
中考数学复习的策略例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(1)将其转化为顶点式:
(2)将其转化为交点式:
(3)开口方向:
(4)对称轴:
(5)顶点坐标:
(6)与X轴的交点坐标 :
(7)与Y轴的交点坐标 :
(8)根据已得的关键点,
画出其图像近似图:
·····1、二次函数关键点坐标1、知识要点梳理:
一般式确定与Y轴交点坐标,顶点式确定顶点坐标及对称轴,交点式确定与X轴交点坐标。
2、方法技巧归纳:
解函数问题,抓关键点坐标
3、解题步骤完善:
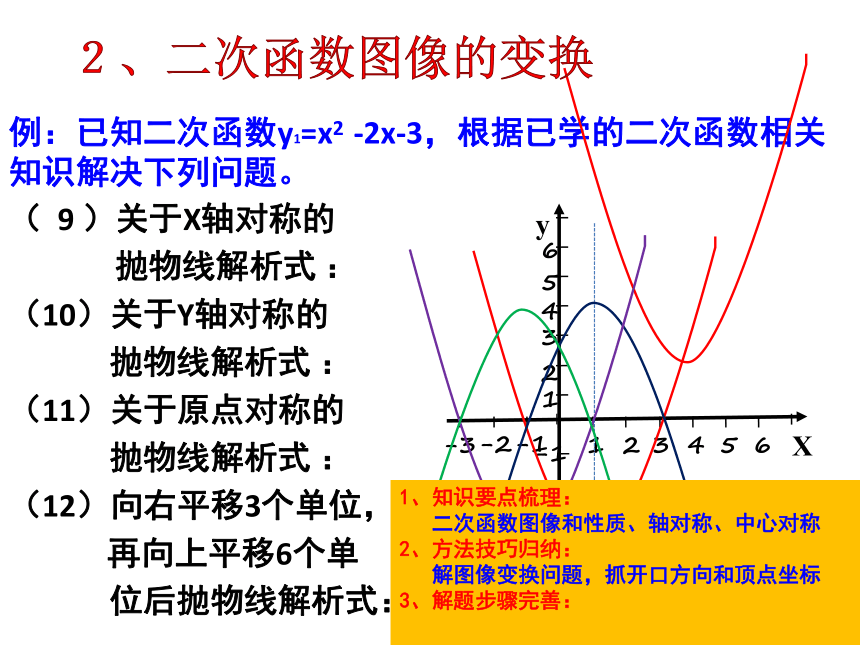
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
( 9 )关于X轴对称的
抛物线解析式 :
(10)关于Y轴对称的
抛物线解析式 :
(11)关于原点对称的
抛物线解析式 :
(12)向右平移3个单位,
再向上平移6个单
位后抛物线解析式:
2、二次函数图像的变换1、知识要点梳理:
二次函数图像和性质、轴对称、中心对称
2、方法技巧归纳:
解图像变换问题,抓开口方向和顶点坐标
3、解题步骤完善:
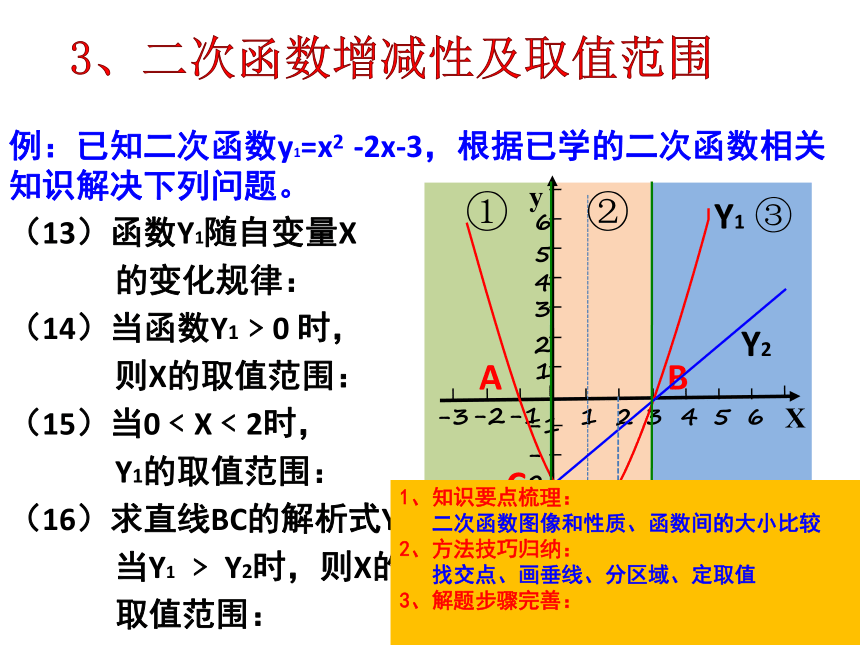
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(13)函数Y1随自变量X
的变化规律:
(14)当函数Y1﹥0 时,
则X的取值范围:
(15)当0﹤X﹤2时,
Y1的取值范围:
(16)求直线BC的解析式Y2,
当Y1 ﹥ Y2时,则X的
取值范围:3、二次函数增减性及取值范围①②③1、知识要点梳理:
二次函数图像和性质、函数间的大小比较
2、方法技巧归纳:
找交点、画垂线、分区域、定取值
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(17)m取何值时,直线Y=m
与抛物线有两个交点?
m取何值时,直线Y=m
与抛物线有一个交点?
m取何值时,直线Y=m
与抛物线没有交点?
4、二次函数中的交点问题1、知识要点梳理:
二次函数图像和性质、图像间的公共点
2、方法技巧归纳:
求交点的问题、就是构建方程组的问题
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(18)若平行于BC的直线与
抛物线 只有一个交点,
求交点D的坐标?
变型题:D5、二次函数的极值问题●在线段BC下方的
抛物线上有一动点D,
当△ BCD的面积最大
时,求点D的坐标?1、知识要点梳理:
二次函数图像和性质、极值
2、方法技巧归纳:
求极值问题,就是构建二次函数问题
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(19)在抛物线上是否存在
一点D,使△ BCD的
面积等于6,若存在,
求出所有符合条件
的点D的坐标。
若不存在,说明理由?ADBCD6、二次函数中的面积计算1、知识要点梳理:
二次函数图像和性质、求面积相关知识
2、方法技巧归纳:
底已知、确定高、画平行线、注意多解
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(20)在对称轴上是否存
在一点P,使以
A、C、P为顶点
的三角形为等腰
三角形,若存在
求出所有符合条
件的点P的坐标。
若不存在,说明理由。PPPPP7、二次函数与等腰三角形1、知识要点梳理:
二次函数图像和性质、等腰三角形知识
2、方法技巧归纳:
依次寻找、防止遗漏、准确解答
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(21)若平行于X轴的直线
与抛物线交于M、N
两点,且以MN为直
径的圆与X轴相切,
求圆的半径?NMONMO8、二次函数于圆(课后探究)1、知识要点梳理:
二次函数图像和性质、圆的切线性质
2、方法技巧归纳:
准确设点的坐标、寻找等量关系列方程
3、解题步骤完善:
谢谢大家
祝老师和同学们
幸福快乐
2、立足于新课标 抓能力培养
3、立足于课堂 抓复习效率
4、立足于教材 抓习题变换
5、立足于反思 抓解题本质
6、立足于数学思想 抓综合运用
中考数学复习的策略例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(1)将其转化为顶点式:
(2)将其转化为交点式:
(3)开口方向:
(4)对称轴:
(5)顶点坐标:
(6)与X轴的交点坐标 :
(7)与Y轴的交点坐标 :
(8)根据已得的关键点,
画出其图像近似图:
·····1、二次函数关键点坐标1、知识要点梳理:
一般式确定与Y轴交点坐标,顶点式确定顶点坐标及对称轴,交点式确定与X轴交点坐标。
2、方法技巧归纳:
解函数问题,抓关键点坐标
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
( 9 )关于X轴对称的
抛物线解析式 :
(10)关于Y轴对称的
抛物线解析式 :
(11)关于原点对称的
抛物线解析式 :
(12)向右平移3个单位,
再向上平移6个单
位后抛物线解析式:
2、二次函数图像的变换1、知识要点梳理:
二次函数图像和性质、轴对称、中心对称
2、方法技巧归纳:
解图像变换问题,抓开口方向和顶点坐标
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(13)函数Y1随自变量X
的变化规律:
(14)当函数Y1﹥0 时,
则X的取值范围:
(15)当0﹤X﹤2时,
Y1的取值范围:
(16)求直线BC的解析式Y2,
当Y1 ﹥ Y2时,则X的
取值范围:3、二次函数增减性及取值范围①②③1、知识要点梳理:
二次函数图像和性质、函数间的大小比较
2、方法技巧归纳:
找交点、画垂线、分区域、定取值
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(17)m取何值时,直线Y=m
与抛物线有两个交点?
m取何值时,直线Y=m
与抛物线有一个交点?
m取何值时,直线Y=m
与抛物线没有交点?
4、二次函数中的交点问题1、知识要点梳理:
二次函数图像和性质、图像间的公共点
2、方法技巧归纳:
求交点的问题、就是构建方程组的问题
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(18)若平行于BC的直线与
抛物线 只有一个交点,
求交点D的坐标?
变型题:D5、二次函数的极值问题●在线段BC下方的
抛物线上有一动点D,
当△ BCD的面积最大
时,求点D的坐标?1、知识要点梳理:
二次函数图像和性质、极值
2、方法技巧归纳:
求极值问题,就是构建二次函数问题
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(19)在抛物线上是否存在
一点D,使△ BCD的
面积等于6,若存在,
求出所有符合条件
的点D的坐标。
若不存在,说明理由?ADBCD6、二次函数中的面积计算1、知识要点梳理:
二次函数图像和性质、求面积相关知识
2、方法技巧归纳:
底已知、确定高、画平行线、注意多解
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(20)在对称轴上是否存
在一点P,使以
A、C、P为顶点
的三角形为等腰
三角形,若存在
求出所有符合条
件的点P的坐标。
若不存在,说明理由。PPPPP7、二次函数与等腰三角形1、知识要点梳理:
二次函数图像和性质、等腰三角形知识
2、方法技巧归纳:
依次寻找、防止遗漏、准确解答
3、解题步骤完善:
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关知识解决下列问题。
(21)若平行于X轴的直线
与抛物线交于M、N
两点,且以MN为直
径的圆与X轴相切,
求圆的半径?NMONMO8、二次函数于圆(课后探究)1、知识要点梳理:
二次函数图像和性质、圆的切线性质
2、方法技巧归纳:
准确设点的坐标、寻找等量关系列方程
3、解题步骤完善:
谢谢大家
祝老师和同学们
幸福快乐
同课章节目录
