等可能情况下的概率计算
图片预览



文档简介
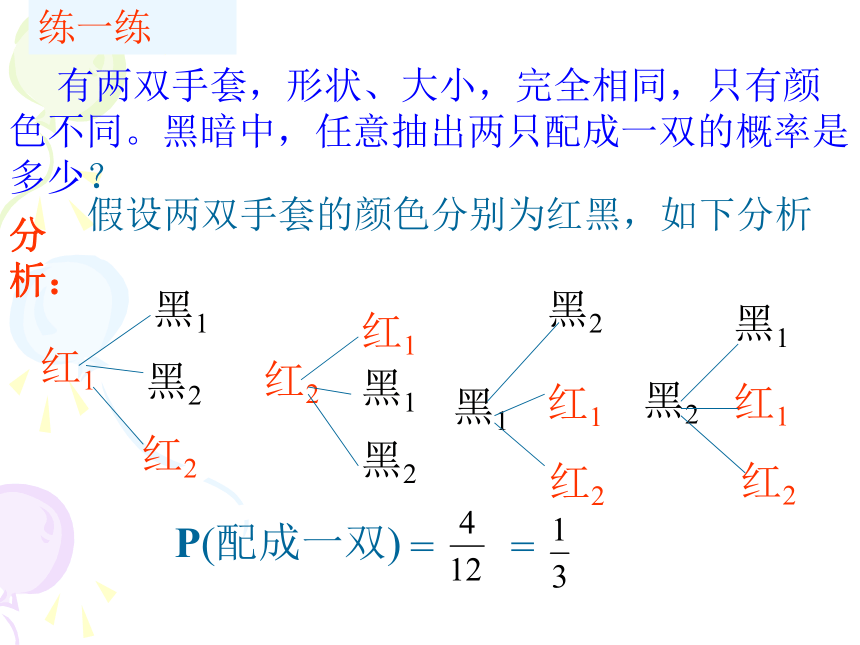
课件13张PPT。等可能情况下的概率计算画树状图求概率1 要清楚所有等可能结果2 要清楚我们所关注的是发生哪个或哪些结果3 概率的计算公式:关注结果数所有等可能的结果数回忆:这节课我们将学习根据树状图理性分析预测概率 有两双手套,形状、大小,完全相同,只有颜色不同。黑暗中,任意抽出两只配成一双的概率是多少?分析:练一练假设两双手套的颜色分别为红黑,如下分析红1
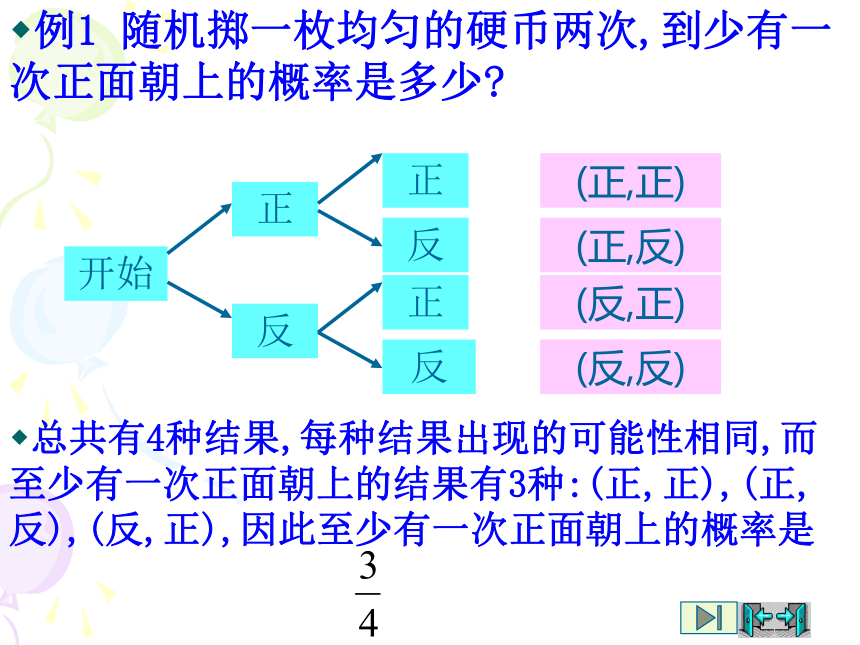
黑1黑2红2红2红1黑1黑1黑1黑2黑2黑2红1红1红2红2P(配成一双)==例1 随机掷一枚均匀的硬币两次,到少有一次正面朝上的概率是多少?总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是开始正反正反正反(正,正)(正,反)(反,正)(反,反)驶向胜利的彼岸例4 抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
?
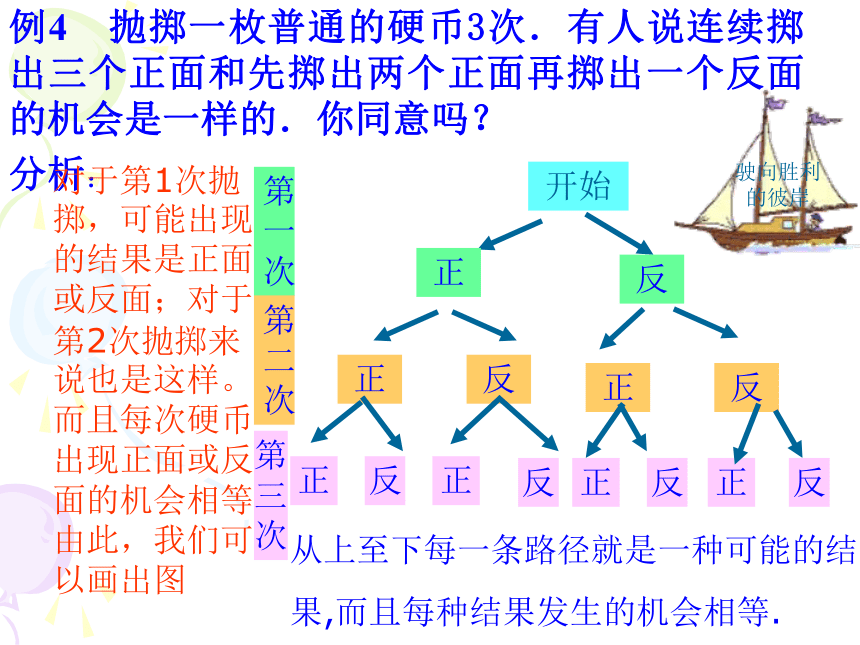
分析:对于第1次抛掷,可能出现的结果是正面或反面;对于第2次抛掷来说也是这样。而且每次硬币出现正面或反面的机会相等。由此,我们可以画出图开始第一次正反第二次正反正反第三次正反正正正反反反从上至下每一条路径就是一种可能的结
果,而且每种结果发生的机会相等.例4 抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
?
解:抛掷一枚普通的硬币三次,共有以下八种机会均等的结果: 正正正 正正反 正反正 反正正 正反反 反正反 反反正 反反反 解P(正正正)=P(正正反)= 所以,这一说法正确. 以上在分析问题的过程中,我们采用了画图的方法,这幅图好象一棵倒立的树,因此我们常把它称为树状图,也称树形图、树图。它可以帮助我们分析问题,而且可以避免重复和遗漏,既直观又条理分明。开始第一次正反第二次正反正反第三次正反正正正反反反有的同学认为:抛三枚普通硬币,硬币落地后只可能出现4种情况(1)全是正面;(2)两正一反;(3)两反一正;(4)全是反面。因些这四个事件出现的概率相等,你同意这种说法吗?解:画树状图分析如下开始硬币1正反硬币2硬币3正反正反正反正反正反正反 口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,会出现哪些可能的结果?问题2 有人说,摸出的不是红球就是白球,因此摸出红球和摸出白球这两个事件是等可能的。
也有人说,如果给小球编号,就可以说:摸出红球,摸出白1球,摸出白2球,这三个事件是等可能的。
你认为哪种说法比较有理呢? 如果将摸出的第一个球放回搅匀再摸出第二个球,两次摸球就可能出现3种可能:(1)都是红球;(2)都是白球;(3)一红一白。
这三个事件发生的概率相等吗? 先用树状图的方法看看有哪些等可能的结果分析开始红白1白2红白1白2红白1白2红白1白2第一次第二次从图中可以看出,一共有9种可能的结果,这9个事件出
现的概率相等,在摸出“两红”、“两白”、“一红一白”这个
事件中,“摸出_____”概率最小,等于___,“摸出一红
一白”和“摸出_____”的概率相等,都是____两红两白思考在分析问题2时,一们同学画出如下图所示的树状图。开始第一次红白红白红白第二次 从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大。
他的分析有道理吗?为什么?
黑1黑2红2红2红1黑1黑1黑1黑2黑2黑2红1红1红2红2P(配成一双)==例1 随机掷一枚均匀的硬币两次,到少有一次正面朝上的概率是多少?总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是开始正反正反正反(正,正)(正,反)(反,正)(反,反)驶向胜利的彼岸例4 抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
?
分析:对于第1次抛掷,可能出现的结果是正面或反面;对于第2次抛掷来说也是这样。而且每次硬币出现正面或反面的机会相等。由此,我们可以画出图开始第一次正反第二次正反正反第三次正反正正正反反反从上至下每一条路径就是一种可能的结
果,而且每种结果发生的机会相等.例4 抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
?
解:抛掷一枚普通的硬币三次,共有以下八种机会均等的结果: 正正正 正正反 正反正 反正正 正反反 反正反 反反正 反反反 解P(正正正)=P(正正反)= 所以,这一说法正确. 以上在分析问题的过程中,我们采用了画图的方法,这幅图好象一棵倒立的树,因此我们常把它称为树状图,也称树形图、树图。它可以帮助我们分析问题,而且可以避免重复和遗漏,既直观又条理分明。开始第一次正反第二次正反正反第三次正反正正正反反反有的同学认为:抛三枚普通硬币,硬币落地后只可能出现4种情况(1)全是正面;(2)两正一反;(3)两反一正;(4)全是反面。因些这四个事件出现的概率相等,你同意这种说法吗?解:画树状图分析如下开始硬币1正反硬币2硬币3正反正反正反正反正反正反 口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,会出现哪些可能的结果?问题2 有人说,摸出的不是红球就是白球,因此摸出红球和摸出白球这两个事件是等可能的。
也有人说,如果给小球编号,就可以说:摸出红球,摸出白1球,摸出白2球,这三个事件是等可能的。
你认为哪种说法比较有理呢? 如果将摸出的第一个球放回搅匀再摸出第二个球,两次摸球就可能出现3种可能:(1)都是红球;(2)都是白球;(3)一红一白。
这三个事件发生的概率相等吗? 先用树状图的方法看看有哪些等可能的结果分析开始红白1白2红白1白2红白1白2红白1白2第一次第二次从图中可以看出,一共有9种可能的结果,这9个事件出
现的概率相等,在摸出“两红”、“两白”、“一红一白”这个
事件中,“摸出_____”概率最小,等于___,“摸出一红
一白”和“摸出_____”的概率相等,都是____两红两白思考在分析问题2时,一们同学画出如下图所示的树状图。开始第一次红白红白红白第二次 从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大。
他的分析有道理吗?为什么?
