新人教A版高中数学必修五3.3.1二元一次不等式(组)与平面区域 同步训练(含答案)
文档属性
| 名称 | 新人教A版高中数学必修五3.3.1二元一次不等式(组)与平面区域 同步训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 610.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-11 18:23:50 | ||
图片预览



文档简介
3.3.1二元一次不等式(组)与平面区域 同步训练(含答案)
1.不等式3x-y-5>0表示的平面区域在直线3x-y-5=0的( )
A.左上方 B.右上方 C.左下方 D.右下方
2.不等式组表示的平面区域是一个( )
A.矩形 B.三角梯形 C.直角形 D.梯形
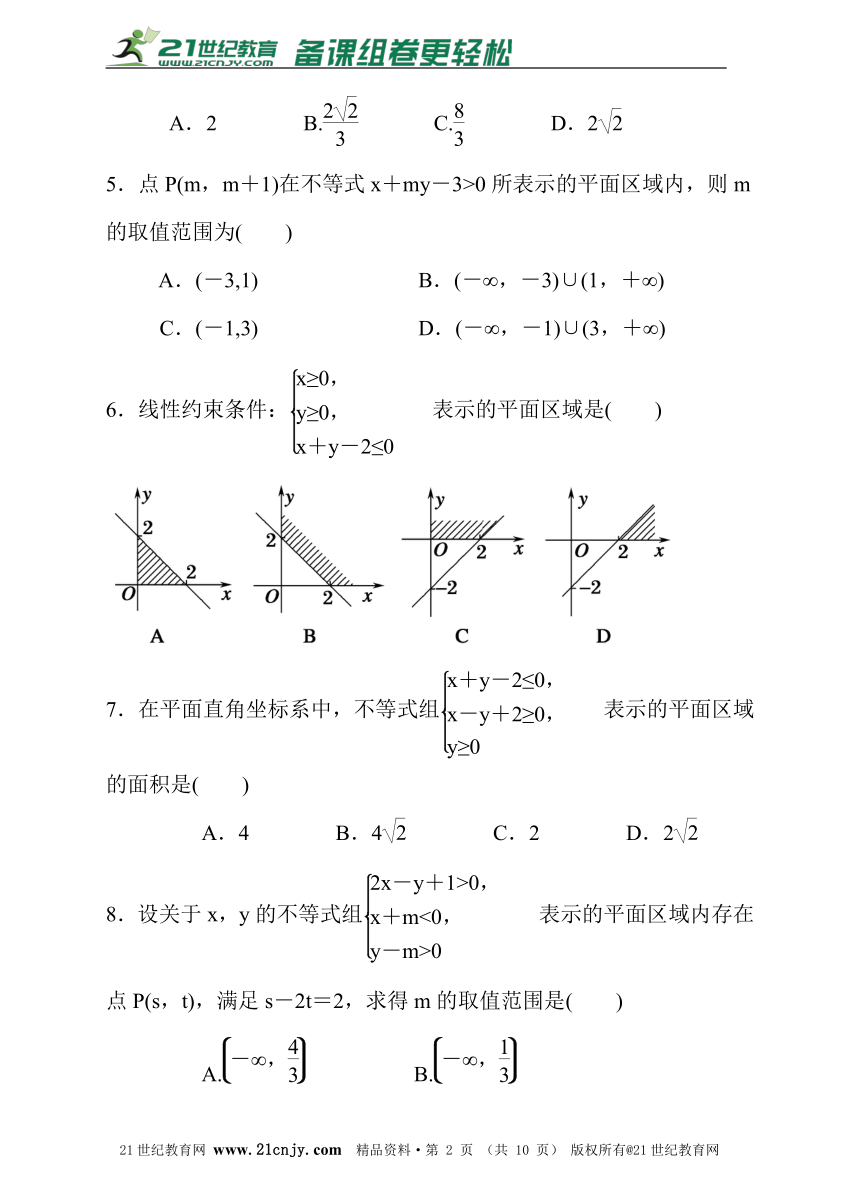
3.能正确表示满足不等式(x-y)(x+2y-3)≥0的点所在的区域的是( )
4.在坐标平面上,不等式组所表示的平面区域的面积为( )
A.2 B. C. D.2
5.点P(m,m+1)在不等式x+my-3>0所表示的平面区域内,则m的取值范围为( )
A.(-3,1) B.(-∞,-3)∪(1,+∞)
C.(-1,3) D.(-∞,-1)∪(3,+∞)
6.线性约束条件:表示的平面区域是( )
7.在平面直角坐标系中,不等式组表示的平面区域的面积是( )
A.4 B.4 C.2 D.2
8.设关于x,y的不等式组表示的平面区域内存在点P(s,t),满足s-2t=2,求得m的取值范围是( )
A. B.
C. D.
9.已知点P(1,-2)及其关于原点的对称点中有且只有一个在不等式2x-ay+1>0表示的平面区域内,则a的取值范围是________.
10.适合下图中阴影部分所示表示的平面区域的不等式组是________.
11.若不等式组表示的平面区域是一个三角形,则m的取值范围是________.
12.若关于x,y的不等式组(k是常数)所表示的平面区域的边界是一个直角三角形,则k=________.21世纪教育网版权所有
13.若x,y满足约束条件则的最大值为________.
14.设不等式组表示的平面区域是M.
(1)求M的面积S;
(2)若点P(t,1)在平面区域M内,求整数t的取值的集合.
15.配制A、B两种饮品,需要甲、乙两种原料,已知配一剂A种饮品需甲原料3 mg,乙原料5 mg;配一剂B种饮品需甲原料5 mg,乙原料4 mg.今有甲原料20 mg,乙原料25 mg,若A、B两种饮品至少各配一剂,问共有多少种不同的配制方法?21cnjy.com
参考答案:
1.解析:将(0,0)代入3x-y-5,得-5<0,(0,0)点在不等式3x-y-5>0表示的平面区域的异侧.则所求区域在对应直线的右下方.答案:D
2.解析:不等式组等价于或答案:D
3.解析:∵(0,0)在(x-y)(x+2y-3)≥0表示的平面区域内,∴可排除
C,D.又∵(-5,0)也在(x-y)(x+2y-3)≥0表示的平面区域内,∴排除B.答案:A
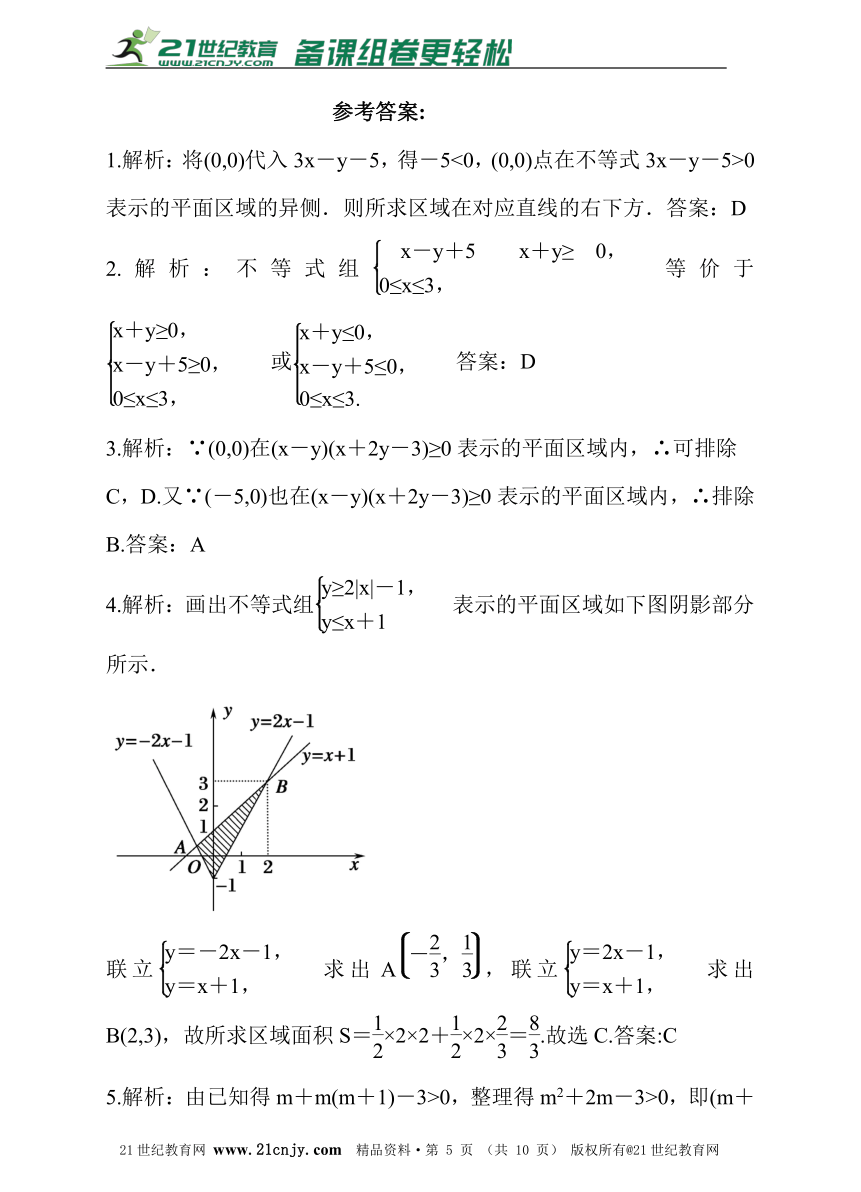
4.解析:画出不等式组表示的平面区域如下图阴影部分所示.
联立求出A,联立求出B(2,3),故所求区域面积S=×2×2+×2×=.故选C.答案:C
5.解析:由已知得m+m(m+1)-3>0,整理得m2+2m-3>0,即(m+3)(m-1)>0,解得m<-3或m>1.故选B.答案:B21·cn·jy·com
6.解析:在直角坐标系内作出直线x+y-2=0,不等式组表示的平面区域就是该直线与两坐标轴所围成的三角形区域,故选A.答案:A
7.解析:首先画出不等式组所表示的平面区域,如图所示的阴影部分.
又B(-2,0),C(2,0),A(0,2)∴S△ABC=×4×2=4.答案:A
8.解析:
作出不等式组表示的平面区域,根据题设条件分析求解当m≥0时,若平面区域存在,则平面区域内的点在第二象限,平面区域内不可能存在点P(s,t)满足s-2t=2,因此m<0.如图所示的阴影部分为不等式组表示的平面区域.要使可行域内包含直线y=x-1上的点,只需可行域边界点(-m,m)在直线y=x-1的下方即可,即m<-m-1,解得m<-.答案:C21教育网
9.解析:设P(1,-2)关于原点的对称点为P′(-1,2),因为点P与点P′有且只有一个适合不等式,www.21-cn-jy.com
所以或得a≥-或a≤-.答案:∪
10.解析:由所给的图形容易知道,点(3,1)在相应的平面区域内,将点(3,1)的坐标分别代入3x+2y-6、2x-3y-6、2x+3y-12中,分别使得3x+2y-6>0、2x-3y-6<0、2x+3y-12<0,再注意到包括各边界,故图中阴影部分所示平面区域的不等式组是答案:【来源:21·世纪·教育·网】
11.解析:
不等式组表示的平面区域如上图所示,当y=a过点A(0,5)时表示的平面区域为三角形,即△ABC,当512.解析:作出不等式组表示的区域如图.由图可知,要使平面区域的边界是一个直角三角形,则k=
答案:-1或0
13.解析:画出可行域如图阴影部分所示,∵表示过点(x,y)与原点(0,0)的直线的斜率,∴点(x,y)在点A处时最大.由得∴A(1,3).∴的最大值为3.答案:32·1·c·n·j·y
14.解:(1)作出平面区域M,它是一个等腰直角三角形(如图所示).
由解得A(4,-4),由解得B(4,12),由解得C(-4,4).于是可得|AB|=16,AB边上的高d=8.∴S=×16×8=64.21·世纪*教育网
(2)由已知得即亦即得t=-1,0,1,2,3,4.故整数t的取值集合是{-1,0,1,2,3,4}.
15.解:设A、B两种饮品分别配x剂、y剂(x,y∈N*).由题意得,
甲原料
乙原料
A饮品/剂
3 mg
5 mg
B饮品/剂
5 mg
4 mg
共计
20 mg
25 mg
则有作出平面区域,如图阴影部分所示,
∵x,y∈N*,∴在区域内作出所有格点(整数点).
由图示可知,区域内的所有整点为(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)、(3,2)、(4,1),共8个点.所以在至少各配一剂的情况下,共有8种不同的配制方法.www-2-1-cnjy-com
1.不等式3x-y-5>0表示的平面区域在直线3x-y-5=0的( )
A.左上方 B.右上方 C.左下方 D.右下方
2.不等式组表示的平面区域是一个( )
A.矩形 B.三角梯形 C.直角形 D.梯形
3.能正确表示满足不等式(x-y)(x+2y-3)≥0的点所在的区域的是( )
4.在坐标平面上,不等式组所表示的平面区域的面积为( )
A.2 B. C. D.2
5.点P(m,m+1)在不等式x+my-3>0所表示的平面区域内,则m的取值范围为( )
A.(-3,1) B.(-∞,-3)∪(1,+∞)
C.(-1,3) D.(-∞,-1)∪(3,+∞)
6.线性约束条件:表示的平面区域是( )
7.在平面直角坐标系中,不等式组表示的平面区域的面积是( )
A.4 B.4 C.2 D.2
8.设关于x,y的不等式组表示的平面区域内存在点P(s,t),满足s-2t=2,求得m的取值范围是( )
A. B.
C. D.
9.已知点P(1,-2)及其关于原点的对称点中有且只有一个在不等式2x-ay+1>0表示的平面区域内,则a的取值范围是________.
10.适合下图中阴影部分所示表示的平面区域的不等式组是________.
11.若不等式组表示的平面区域是一个三角形,则m的取值范围是________.
12.若关于x,y的不等式组(k是常数)所表示的平面区域的边界是一个直角三角形,则k=________.21世纪教育网版权所有
13.若x,y满足约束条件则的最大值为________.
14.设不等式组表示的平面区域是M.
(1)求M的面积S;
(2)若点P(t,1)在平面区域M内,求整数t的取值的集合.
15.配制A、B两种饮品,需要甲、乙两种原料,已知配一剂A种饮品需甲原料3 mg,乙原料5 mg;配一剂B种饮品需甲原料5 mg,乙原料4 mg.今有甲原料20 mg,乙原料25 mg,若A、B两种饮品至少各配一剂,问共有多少种不同的配制方法?21cnjy.com
参考答案:
1.解析:将(0,0)代入3x-y-5,得-5<0,(0,0)点在不等式3x-y-5>0表示的平面区域的异侧.则所求区域在对应直线的右下方.答案:D
2.解析:不等式组等价于或答案:D
3.解析:∵(0,0)在(x-y)(x+2y-3)≥0表示的平面区域内,∴可排除
C,D.又∵(-5,0)也在(x-y)(x+2y-3)≥0表示的平面区域内,∴排除B.答案:A
4.解析:画出不等式组表示的平面区域如下图阴影部分所示.
联立求出A,联立求出B(2,3),故所求区域面积S=×2×2+×2×=.故选C.答案:C
5.解析:由已知得m+m(m+1)-3>0,整理得m2+2m-3>0,即(m+3)(m-1)>0,解得m<-3或m>1.故选B.答案:B21·cn·jy·com
6.解析:在直角坐标系内作出直线x+y-2=0,不等式组表示的平面区域就是该直线与两坐标轴所围成的三角形区域,故选A.答案:A
7.解析:首先画出不等式组所表示的平面区域,如图所示的阴影部分.
又B(-2,0),C(2,0),A(0,2)∴S△ABC=×4×2=4.答案:A
8.解析:
作出不等式组表示的平面区域,根据题设条件分析求解当m≥0时,若平面区域存在,则平面区域内的点在第二象限,平面区域内不可能存在点P(s,t)满足s-2t=2,因此m<0.如图所示的阴影部分为不等式组表示的平面区域.要使可行域内包含直线y=x-1上的点,只需可行域边界点(-m,m)在直线y=x-1的下方即可,即m<-m-1,解得m<-.答案:C21教育网
9.解析:设P(1,-2)关于原点的对称点为P′(-1,2),因为点P与点P′有且只有一个适合不等式,www.21-cn-jy.com
所以或得a≥-或a≤-.答案:∪
10.解析:由所给的图形容易知道,点(3,1)在相应的平面区域内,将点(3,1)的坐标分别代入3x+2y-6、2x-3y-6、2x+3y-12中,分别使得3x+2y-6>0、2x-3y-6<0、2x+3y-12<0,再注意到包括各边界,故图中阴影部分所示平面区域的不等式组是答案:【来源:21·世纪·教育·网】
11.解析:
不等式组表示的平面区域如上图所示,当y=a过点A(0,5)时表示的平面区域为三角形,即△ABC,当5
答案:-1或0
13.解析:画出可行域如图阴影部分所示,∵表示过点(x,y)与原点(0,0)的直线的斜率,∴点(x,y)在点A处时最大.由得∴A(1,3).∴的最大值为3.答案:32·1·c·n·j·y
14.解:(1)作出平面区域M,它是一个等腰直角三角形(如图所示).
由解得A(4,-4),由解得B(4,12),由解得C(-4,4).于是可得|AB|=16,AB边上的高d=8.∴S=×16×8=64.21·世纪*教育网
(2)由已知得即亦即得t=-1,0,1,2,3,4.故整数t的取值集合是{-1,0,1,2,3,4}.
15.解:设A、B两种饮品分别配x剂、y剂(x,y∈N*).由题意得,
甲原料
乙原料
A饮品/剂
3 mg
5 mg
B饮品/剂
5 mg
4 mg
共计
20 mg
25 mg
则有作出平面区域,如图阴影部分所示,
∵x,y∈N*,∴在区域内作出所有格点(整数点).
由图示可知,区域内的所有整点为(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)、(3,2)、(4,1),共8个点.所以在至少各配一剂的情况下,共有8种不同的配制方法.www-2-1-cnjy-com
