5.3应用一元一次方程——水箱变高了 同步练习(含解析)
文档属性
| 名称 | 5.3应用一元一次方程——水箱变高了 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 30.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-11 17:30:05 | ||
图片预览

文档简介
5.3应用一元一次方程---水箱变高了
A基础知识训练
1.(2016?南平中考)闽北某村原有林地120公顷,旱地60公顷,为适应产业结构调整,需把一部分旱地改造为林地,改造后,旱地面积占林地面积的20%,设把x公顷旱地改造为林地,则可列方程为( )? A.60-x=20%(120+x)? B.60+x=20%×120? C.180-x=20%(60+x)? D.60-x=20%×1202-1-c-n-j-y
2.(2016?宽城区期中)某小区在规划设计时,准备在两幢楼房之间,设置一块周长为120米的长方形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,下面列出的方程正确的是( )? A.2(x-10)=120? B.2[x+(x-10)]=120? C.2(x+10)=120? D.2[x+(x+10)]=120
3.(2016·临沂质检)用一根20m长的铁丝围成一个一边长为4m的长方形,则围成的长方形的面积是( ) 21·cn·jy·com
A. 6m2 B. 20m2 C.24m2 D. 80m2
4.(2016·青岛质检) 将一个底面直径是10cm,高8cm 的“矮胖”形圆柱锻造成直径为4cm,的“瘦长”形圆柱,高变成了多少?设高变成 21*cnjy*com
xcm,根据题意列方程为 .
5.(2016·连云港期末)如图,小明从一个正方形纸片上剪下一个宽为6cm的长条后,再从剩下的纸片上剪下一个宽为8cm的长条.如果两次剪下的长条面积正好相等,那么原正方形的边长是 .21教育网
B基本技能训练
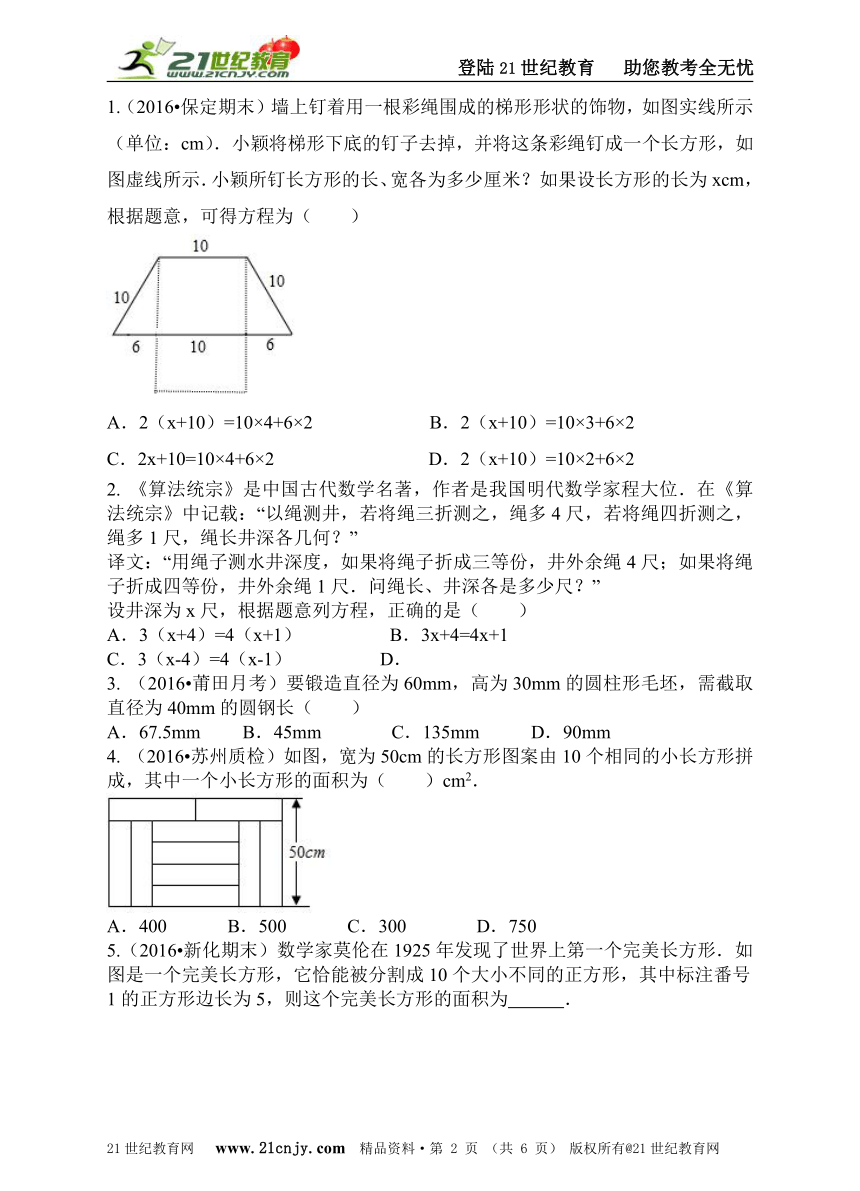
1.(2016?保定期末)墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )? A.2(x+10)=10×4+6×2? B.2(x+10)=10×3+6×2? C.2x+10=10×4+6×2? D.2(x+10)=10×2+6×2
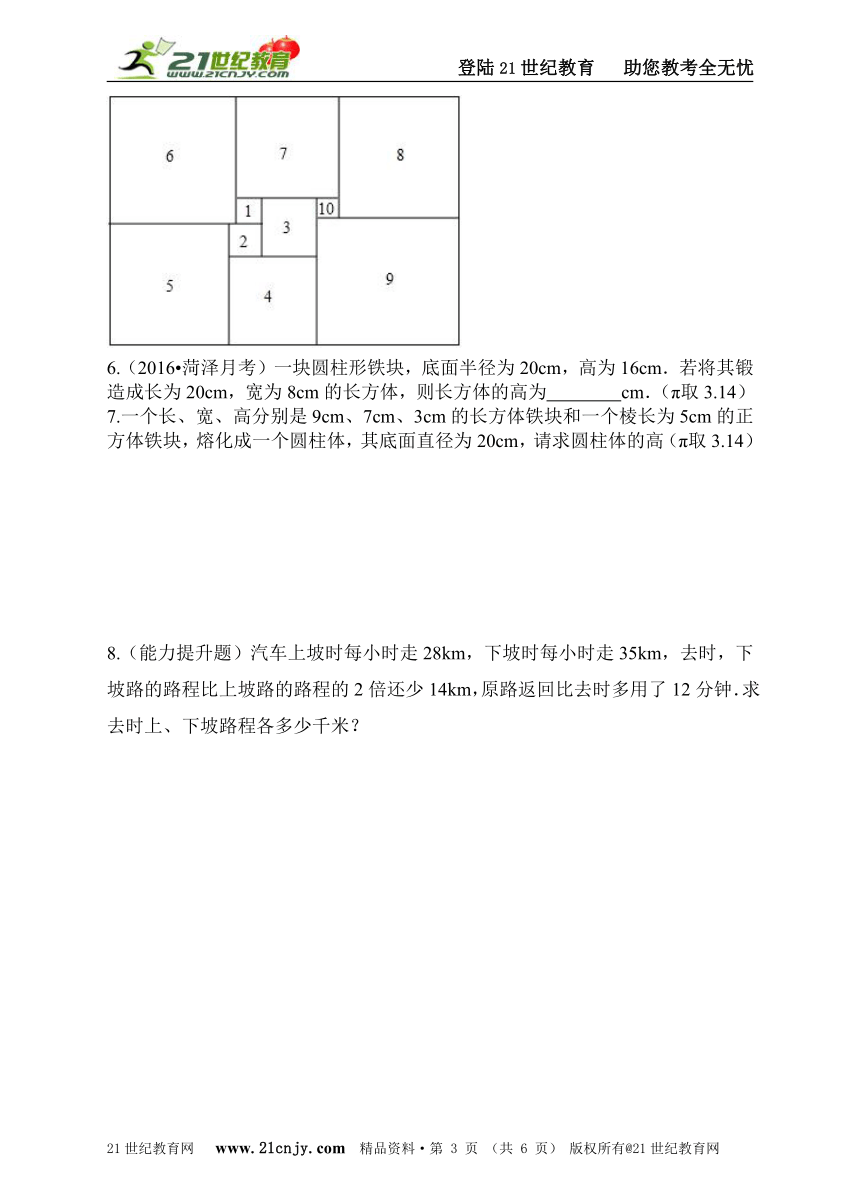
2. 《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”? 译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”? 设井深为x尺,根据题意列方程,正确的是( )? A.3(x+4)=4(x+1)? B.3x+4=4x+1? C.3(x-4)=4(x-1)? D.? 3. (2016?莆田月考)要锻造直径为60mm,高为30mm的圆柱形毛坯,需截取直径为40mm的圆钢长( )? A.67.5mm? B.45mm? C.135mm? D.90mm? 4. (2016?苏州质检)如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.? A.400? B.500? C.300? D.750? 5.(2016?新化期末)数学家莫伦在1925年发现了世界上第一个完美长方形.如图是一个完美长方形,它恰能被分割成10个大小不同的正方形,其中标注番号1的正方形边长为5,则这个完美长方形的面积为 .? 6.(2016?菏泽月考)一块圆柱形铁块,底面半径为20cm,高为16cm.若将其锻造成长为20cm,宽为8cm的长方体,则长方体的高为 cm.(π取3.14)? 7.一个长、宽、高分别是9cm、7cm、3cm的长方体铁块和一个棱长为5cm的正方体铁块,熔化成一个圆柱体,其底面直径为20cm,请求圆柱体的高(π取3.14)
8.(能力提升题)汽车上坡时每小时走28km,下坡时每小时走35km,去时,下坡路的路程比上坡路的路程的2倍还少14km,原路返回比去时多用了12分钟.求去时上、下坡路程各多少千米?? 21cnjy.com
附答案:
5.3应用一元一次方程---水箱变高了
A基础知识训练
1.【解析】选A.设把x公顷旱地改造为林地,
由题意得,60-x=20%(120+x)
2.【解析】选D. 设绿地的宽为x米,则长为(x+10)米,
根据题意,2[x+(x+10)]=120
3.【解析】选C.设长方形的另一边为xm,
根据题意得2(x+4)=20,解得x=6,
所以长方形的面积为:4×6=24(m2).
4.【解析】“矮胖”形圆柱的体积为:,
“瘦长”形圆柱的体积为:,根据变化前后的体积不变可列方程为:=.
答案:=.
5.【解析】设原正方形的边长为xcm,
根据题意得6x=8(x-6)
解得x=24.
所以原正方形的边长是24cm.
答案:24cm
B基本技能训练
1.【解析】选A.设长方形的长为xcm,
根据题意,2(x+10)=10×4+6×2
2.【解析】选A. 设井深为x尺,
根据题意列方程,3(x+4)=4(x+1)
3.【解析】选A.设需截取直径为40mm的圆钢长xmm,? 得方程:π×()2×30=π×()2×x,?21世纪教育网版权所有
解得x=67.5.?
4.【解析】选A.设小长方形的长为xcm,则宽为(50-x)cm,根据题意可得:? 2x=x+4(50-x),? 解得:x=40,? 故50-x=10(cm).? 则一个小长方形的面积为:10×40=400(cm2).?www.21-cn-jy.com
5.【解析】设标注番号2的正方形边长是x,标注番号1的正方形边长为5,? 则第3个正方形的边长是x+5;? 第4个正方形的边长是x+x+5=2x+5;? 第5个正方形的边长是x+2x+5=3x+5;? 第6个正方形的边长是3x+5+x-5=4x;? 2·1·c·n·j·y
第7个正方形的边长是4x-5;? 第10个正方形的边长是4x-5-5-(x+5)=3x-15;? 第8个正方形的边长是4x-5+3x-15=7x-20;? 第9个正方形的边长是3x-15+7x-20=10x-35;? 根据题意得3x+5+4x=7x-20+10x-35,? 解得x=6,? 则完美长方形的宽为3x+5+4x=7x+5=47,? 完美长方形的长为4x+4x-5+7x-20=15x-25=65,? 所以完美长方形的面积为65×47=3055.? 答案:3055【来源:21·世纪·教育·网】
6.【解析】设长方体的高为xcm,? 则π×202×16=20×8×x,? 解得x≈125.6? 答案:125.621·世纪*教育网
7.解;设圆柱体的高为xcm,
根据题意得,
解得x=1.
所以圆柱的高为1cm.
8.解:设去时上坡路为x千米,则下坡路为(2x-14)千米,
根据题意得:?,
解得:x=42, 则2x-14=2×42-14=70,? 答:去时上、下坡路程各为42千米、70千米.www-2-1-cnjy-com
A基础知识训练
1.(2016?南平中考)闽北某村原有林地120公顷,旱地60公顷,为适应产业结构调整,需把一部分旱地改造为林地,改造后,旱地面积占林地面积的20%,设把x公顷旱地改造为林地,则可列方程为( )? A.60-x=20%(120+x)? B.60+x=20%×120? C.180-x=20%(60+x)? D.60-x=20%×1202-1-c-n-j-y
2.(2016?宽城区期中)某小区在规划设计时,准备在两幢楼房之间,设置一块周长为120米的长方形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,下面列出的方程正确的是( )? A.2(x-10)=120? B.2[x+(x-10)]=120? C.2(x+10)=120? D.2[x+(x+10)]=120
3.(2016·临沂质检)用一根20m长的铁丝围成一个一边长为4m的长方形,则围成的长方形的面积是( ) 21·cn·jy·com
A. 6m2 B. 20m2 C.24m2 D. 80m2
4.(2016·青岛质检) 将一个底面直径是10cm,高8cm 的“矮胖”形圆柱锻造成直径为4cm,的“瘦长”形圆柱,高变成了多少?设高变成 21*cnjy*com
xcm,根据题意列方程为 .
5.(2016·连云港期末)如图,小明从一个正方形纸片上剪下一个宽为6cm的长条后,再从剩下的纸片上剪下一个宽为8cm的长条.如果两次剪下的长条面积正好相等,那么原正方形的边长是 .21教育网
B基本技能训练
1.(2016?保定期末)墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )? A.2(x+10)=10×4+6×2? B.2(x+10)=10×3+6×2? C.2x+10=10×4+6×2? D.2(x+10)=10×2+6×2
2. 《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”? 译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”? 设井深为x尺,根据题意列方程,正确的是( )? A.3(x+4)=4(x+1)? B.3x+4=4x+1? C.3(x-4)=4(x-1)? D.? 3. (2016?莆田月考)要锻造直径为60mm,高为30mm的圆柱形毛坯,需截取直径为40mm的圆钢长( )? A.67.5mm? B.45mm? C.135mm? D.90mm? 4. (2016?苏州质检)如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.? A.400? B.500? C.300? D.750? 5.(2016?新化期末)数学家莫伦在1925年发现了世界上第一个完美长方形.如图是一个完美长方形,它恰能被分割成10个大小不同的正方形,其中标注番号1的正方形边长为5,则这个完美长方形的面积为 .? 6.(2016?菏泽月考)一块圆柱形铁块,底面半径为20cm,高为16cm.若将其锻造成长为20cm,宽为8cm的长方体,则长方体的高为 cm.(π取3.14)? 7.一个长、宽、高分别是9cm、7cm、3cm的长方体铁块和一个棱长为5cm的正方体铁块,熔化成一个圆柱体,其底面直径为20cm,请求圆柱体的高(π取3.14)
8.(能力提升题)汽车上坡时每小时走28km,下坡时每小时走35km,去时,下坡路的路程比上坡路的路程的2倍还少14km,原路返回比去时多用了12分钟.求去时上、下坡路程各多少千米?? 21cnjy.com
附答案:
5.3应用一元一次方程---水箱变高了
A基础知识训练
1.【解析】选A.设把x公顷旱地改造为林地,
由题意得,60-x=20%(120+x)
2.【解析】选D. 设绿地的宽为x米,则长为(x+10)米,
根据题意,2[x+(x+10)]=120
3.【解析】选C.设长方形的另一边为xm,
根据题意得2(x+4)=20,解得x=6,
所以长方形的面积为:4×6=24(m2).
4.【解析】“矮胖”形圆柱的体积为:,
“瘦长”形圆柱的体积为:,根据变化前后的体积不变可列方程为:=.
答案:=.
5.【解析】设原正方形的边长为xcm,
根据题意得6x=8(x-6)
解得x=24.
所以原正方形的边长是24cm.
答案:24cm
B基本技能训练
1.【解析】选A.设长方形的长为xcm,
根据题意,2(x+10)=10×4+6×2
2.【解析】选A. 设井深为x尺,
根据题意列方程,3(x+4)=4(x+1)
3.【解析】选A.设需截取直径为40mm的圆钢长xmm,? 得方程:π×()2×30=π×()2×x,?21世纪教育网版权所有
解得x=67.5.?
4.【解析】选A.设小长方形的长为xcm,则宽为(50-x)cm,根据题意可得:? 2x=x+4(50-x),? 解得:x=40,? 故50-x=10(cm).? 则一个小长方形的面积为:10×40=400(cm2).?www.21-cn-jy.com
5.【解析】设标注番号2的正方形边长是x,标注番号1的正方形边长为5,? 则第3个正方形的边长是x+5;? 第4个正方形的边长是x+x+5=2x+5;? 第5个正方形的边长是x+2x+5=3x+5;? 第6个正方形的边长是3x+5+x-5=4x;? 2·1·c·n·j·y
第7个正方形的边长是4x-5;? 第10个正方形的边长是4x-5-5-(x+5)=3x-15;? 第8个正方形的边长是4x-5+3x-15=7x-20;? 第9个正方形的边长是3x-15+7x-20=10x-35;? 根据题意得3x+5+4x=7x-20+10x-35,? 解得x=6,? 则完美长方形的宽为3x+5+4x=7x+5=47,? 完美长方形的长为4x+4x-5+7x-20=15x-25=65,? 所以完美长方形的面积为65×47=3055.? 答案:3055【来源:21·世纪·教育·网】
6.【解析】设长方体的高为xcm,? 则π×202×16=20×8×x,? 解得x≈125.6? 答案:125.621·世纪*教育网
7.解;设圆柱体的高为xcm,
根据题意得,
解得x=1.
所以圆柱的高为1cm.
8.解:设去时上坡路为x千米,则下坡路为(2x-14)千米,
根据题意得:?,
解得:x=42, 则2x-14=2×42-14=70,? 答:去时上、下坡路程各为42千米、70千米.www-2-1-cnjy-com
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
