3.4.1实际问题与一元一次方程(分配和配套问题)课件(共17张PPT)
文档属性
| 名称 | 3.4.1实际问题与一元一次方程(分配和配套问题)课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 232.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 13:35:31 | ||
图片预览






文档简介
课件17张PPT。例1.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?分析:
设这个班有x名学生.每人分3本,共分出3x本,加上剩余的20本,这批书共 ____ 本;每人分4本,需要___本,减去缺的25本,这批书共______本.这批书的总数是一个定值,表示它的两个式子应相等.(3x+20)4x(4x – 25) 这批书的总数是一个定值,表示它的两个式子相等. 3x+20 = 4x-25.合并,得解:设这个班有x名学生,根据题意列 方程,得 - x = -45.系数化为1,得x = 45.答:这个班有45名学生.移项,得3 x -4 x = -25-20.练习1.有一个班的同学去某游乐园划船,他们算了一下,如果增加一条船,正好每条船坐6人;如果减少一条船,正好每条船坐 9人。这个班共有多少名学生?表示同一个量的两个不同式子相等例2.某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母.为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少工人生产螺母? 分析:
(1)如果设x名工人生产螺钉,则 名工人生产螺母;
(2)为了使每天的产品刚好配套.应使生产的螺母恰好是螺钉数量的 。 两个等量关系的问题:利用第一个等量关系设未知数,第二个等量关系列方程。 (22-x)2倍解:设分配x名工人生产螺钉,其余(22-x)名工人生产螺母.则
2×1 200x=2 000(22-x).
去括号,得 2 400x=44 000-2 000x.
移项及合并,得 4 400x=44 000.
系数化为1,得 x=10.
生产螺母的人数为 22-x=12.
答:应分配10名工人生产螺钉,12名工人生产螺母.一元一次方程的解(x=a)实际问题
的答案 一元一次方程2000(22-x)=2×1200x x=10
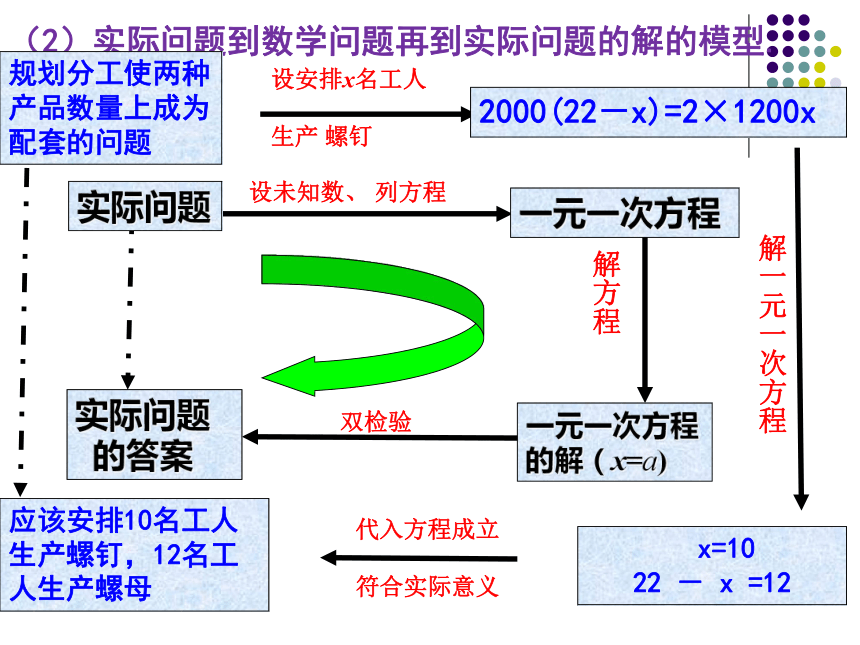
22 - x =12应该安排10名工人生产螺钉,12名工人生产螺母(2)实际问题到数学问题再到实际问题的解的模型.实际问题规划分工使两种产品数量上成为配套的问题列方程解应用题的一般步骤:审:分析题中已知什么,未知什么,明确各量 之间的关系。
找:找等量关系(列方程的关键);设:设未知数,一般是求什么就设什么为x,
但有时也可以间接设未知数;列:把相等关系左右两边的量用含有未知数的
代数式表示出来,列出方程;
解:求出未知数的值;验:看方程的解是否正确以及是否符合题意;
答:写出答案(包括单位)。练习1.某水利工地派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?分析:
(1)如果设x名挖土,则 名运土;
(2)为了使挖出的土及时运走.应使
挖出土的数量 运走土的数量 两个等量关系的问题:利用第一个等量关系设未知数,第二个等量关系列方程。 (48-x)等于练习2.某车间每天能生产甲种零件120个,或乙种零件100个,甲、乙两种零件分别取3个、2个才能配成一套,现要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数?分析:
(1)如果设x天生产甲种零件,则 天生产乙种零件;
(2)为了使30天内生产最多的成套产品.应使
甲种零件数量:乙种零件数量= 。 两个等量关系的问题:利用第一个等量关系设未知数,第二个等量关系列方程。 (30-x)3:2用一元一次方程分析和解决实际问题的基本过程如下:实际问题数学问题
(一元一次方程)实际问题的答案数学问题的解
(x=a)列方程检验解方程抓住配套关系,设出未知数,根据配套关系列出方程,通过解方程来解决问题小结:这节课我们复习了分配与配套问题问题,
归纳如下: 一套仪器由一个A部件和三个B部件构成。用1立方米钢材可做40个A部件或240个B部件。现要用6立方米钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
某车间有工人85人,平均每人每天可以加工大齿轮8个或小齿轮10个,又知1个大齿轮和三个小齿轮配为一套,问应如何安排劳力使生产的产品刚好成套? 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套? 七年级170名学生参加植树活动,如果每个男生能挖树坑3个,每个女生能种树7棵,正好能使每个树坑种上一棵树,则应该安排男生、女生各有多少人? 某服装厂要生产某种型号的学生校服,已知3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存这种布料600m,应如何分配布料做上衣和做裤子才能恰好配套?可以生产多少套衣服?
设这个班有x名学生.每人分3本,共分出3x本,加上剩余的20本,这批书共 ____ 本;每人分4本,需要___本,减去缺的25本,这批书共______本.这批书的总数是一个定值,表示它的两个式子应相等.(3x+20)4x(4x – 25) 这批书的总数是一个定值,表示它的两个式子相等. 3x+20 = 4x-25.合并,得解:设这个班有x名学生,根据题意列 方程,得 - x = -45.系数化为1,得x = 45.答:这个班有45名学生.移项,得3 x -4 x = -25-20.练习1.有一个班的同学去某游乐园划船,他们算了一下,如果增加一条船,正好每条船坐6人;如果减少一条船,正好每条船坐 9人。这个班共有多少名学生?表示同一个量的两个不同式子相等例2.某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母.为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少工人生产螺母? 分析:
(1)如果设x名工人生产螺钉,则 名工人生产螺母;
(2)为了使每天的产品刚好配套.应使生产的螺母恰好是螺钉数量的 。 两个等量关系的问题:利用第一个等量关系设未知数,第二个等量关系列方程。 (22-x)2倍解:设分配x名工人生产螺钉,其余(22-x)名工人生产螺母.则
2×1 200x=2 000(22-x).
去括号,得 2 400x=44 000-2 000x.
移项及合并,得 4 400x=44 000.
系数化为1,得 x=10.
生产螺母的人数为 22-x=12.
答:应分配10名工人生产螺钉,12名工人生产螺母.一元一次方程的解(x=a)实际问题
的答案 一元一次方程2000(22-x)=2×1200x x=10
22 - x =12应该安排10名工人生产螺钉,12名工人生产螺母(2)实际问题到数学问题再到实际问题的解的模型.实际问题规划分工使两种产品数量上成为配套的问题列方程解应用题的一般步骤:审:分析题中已知什么,未知什么,明确各量 之间的关系。
找:找等量关系(列方程的关键);设:设未知数,一般是求什么就设什么为x,
但有时也可以间接设未知数;列:把相等关系左右两边的量用含有未知数的
代数式表示出来,列出方程;
解:求出未知数的值;验:看方程的解是否正确以及是否符合题意;
答:写出答案(包括单位)。练习1.某水利工地派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?分析:
(1)如果设x名挖土,则 名运土;
(2)为了使挖出的土及时运走.应使
挖出土的数量 运走土的数量 两个等量关系的问题:利用第一个等量关系设未知数,第二个等量关系列方程。 (48-x)等于练习2.某车间每天能生产甲种零件120个,或乙种零件100个,甲、乙两种零件分别取3个、2个才能配成一套,现要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数?分析:
(1)如果设x天生产甲种零件,则 天生产乙种零件;
(2)为了使30天内生产最多的成套产品.应使
甲种零件数量:乙种零件数量= 。 两个等量关系的问题:利用第一个等量关系设未知数,第二个等量关系列方程。 (30-x)3:2用一元一次方程分析和解决实际问题的基本过程如下:实际问题数学问题
(一元一次方程)实际问题的答案数学问题的解
(x=a)列方程检验解方程抓住配套关系,设出未知数,根据配套关系列出方程,通过解方程来解决问题小结:这节课我们复习了分配与配套问题问题,
归纳如下: 一套仪器由一个A部件和三个B部件构成。用1立方米钢材可做40个A部件或240个B部件。现要用6立方米钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
某车间有工人85人,平均每人每天可以加工大齿轮8个或小齿轮10个,又知1个大齿轮和三个小齿轮配为一套,问应如何安排劳力使生产的产品刚好成套? 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套? 七年级170名学生参加植树活动,如果每个男生能挖树坑3个,每个女生能种树7棵,正好能使每个树坑种上一棵树,则应该安排男生、女生各有多少人? 某服装厂要生产某种型号的学生校服,已知3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,库内存这种布料600m,应如何分配布料做上衣和做裤子才能恰好配套?可以生产多少套衣服?
