上海市八中学课件：点到直线的距离

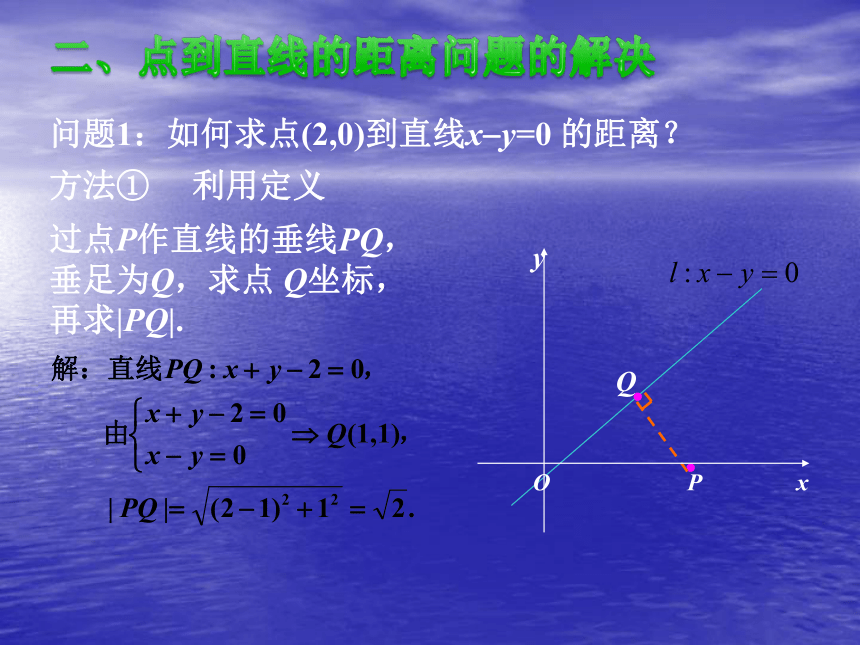
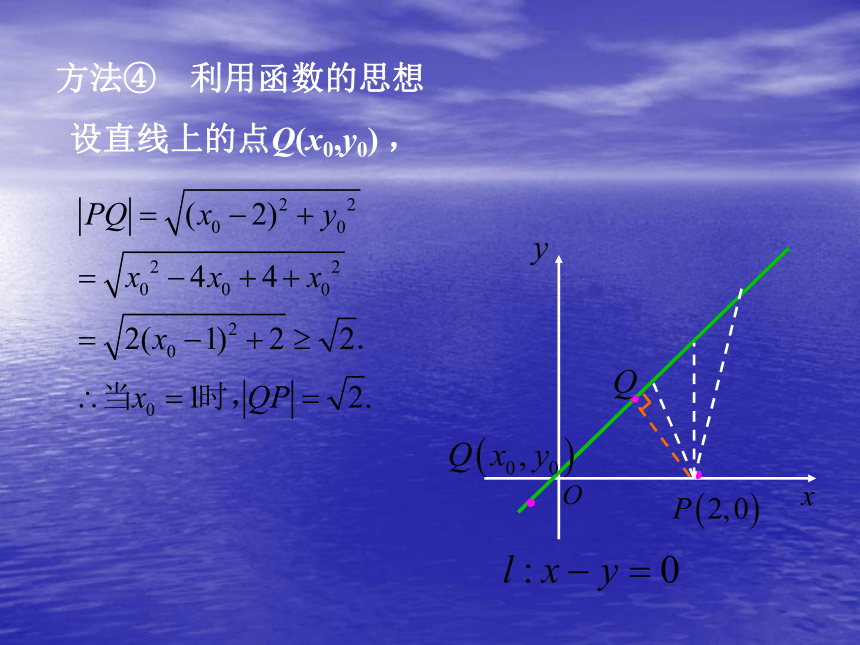
课件11张PPT。点到直线的距离上海市八中学一、问题情境平面几何中点到直线的距离是怎样定义的？（1）点与直线的位置关系点在直线上和点在直线外两种位置关系。用点的坐标是否满足直线方程来判断点与直线的位置关系。（2）两点A(a1,b1)、B(a2,b2)之间的距离公式（3）点P到直线l的距离过点P作l的垂线，P与垂足P0之间的距离。问题1：如何求点(2,0)到直线x?y=0 的距离？·方法① 　利用定义过点P作直线的垂线PQ，垂足为Q，求点 Q坐标，再求|PQ|.·Q二、点到直线的距离问题的解决方法③　利用直角三角形的面积公式方法②　利用三角函数|PQ|=|OP|sin450=2sin450=R···方法④ 利用函数的思想设直线上的点Q(x0,y0) ，方法①　直接法·问题2 求点P0(x0,y0)到直线l:ax+by+c=0(a2+b2?0)的距离。点P0、Q 之间的距离|P0Q|（P0到l的距离）思路简单运算繁琐?P0l:ax+by+c=0方法②　面积法 ··y面积法求出 |PQ| P(x0,y0)l:ax+by+c=0过 程 设 计O xyl:ax+by+c=0?P(x0,y0)Q方法③ 向量法设点P在直线l上的射影为Q(xQ,yQ)，点Q的坐标满足直线l的方程。三、简单应用例. 求点P(?1,2)到下列直线的距离：
（1）y=?2x+10；（2）3x=2；（3）2y+1=0用点到直线的距离公式，先将直线方程化为一般式。?P特殊状态的直线可数形结合解决。?P四、课堂练习求点P(3,1)到下列直线的距离
（1）3x+4y?5=0；（2）5x+2=0；（3）3y?1=02. 已知△ABC的三个顶点坐标分别为A(2,1)、B(5,3)、C(?1,5)，求△ABC的 BC边上的高。 点A到BC所在直线的距离。解：直线BC的方程为x+3y?14=0,