上海市八中学课件:直线方程复习(一)
图片预览




文档简介
课件10张PPT。直线方程复习(一)上海市八中学问题1 确定一条直线的要素:1. 定位2. 定向一、知识点回顾方向向量、法向量、另一点、
斜率 (倾斜角不是直角)。这便是直线的点方向式、点法向式、点斜式
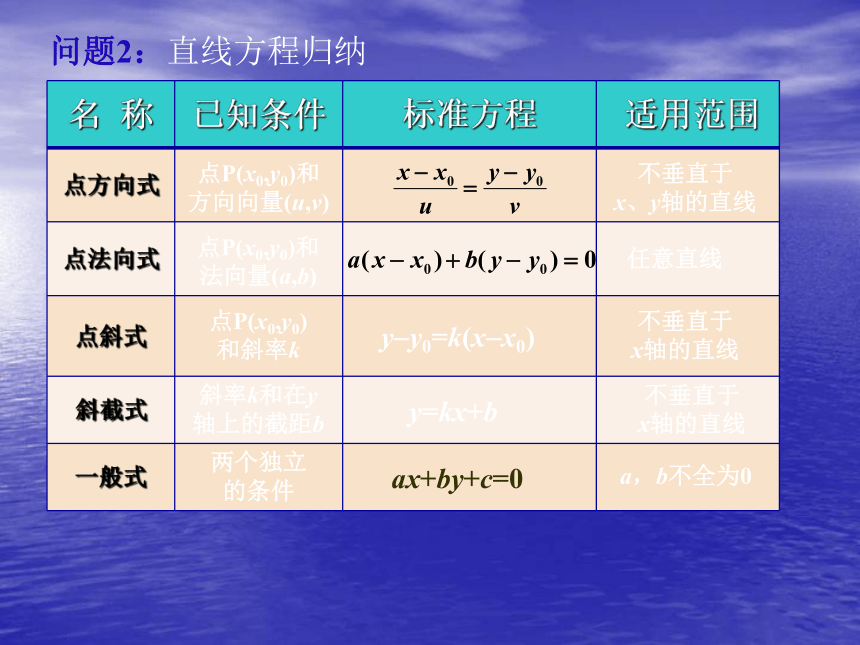
的由来,斜截式是点斜式的特例。直线过定点方程ax+by+c=0(a,b不全为0)叫做直线方程的一般式,任何一条直线的方程都可以化成一般式。问题2 直线的一般式方程问题2:直线方程归纳点P(x0,y0)和方向向量(u,v)不垂直于
x、y轴的直线点P(x0,y0)和法向量(a,b)任意直线点P(x0,y0)
和斜率ky?y0=k(x?x0)不垂直于
x轴的直线斜率k和在y轴上的截距by=kx+b不垂直于
x轴的直线两个独立的条件ax+by+c=0a,b不全为0二、应用举例例:已知直线l过点P(?3,4),求满足下列条件的直线l的方程:(1)过另一点Q(a,1);P(?3,4)?1解:当a=?3时,l:x=?3;当a??3时,直线l的法向量为(3,a+3),直线l的方程为3(x+3)+(a+3)(y?4)=0.(2)坐标原点O到直线l的距离最大;分析:当OP与直线l垂直时,点O
到直线l的距离最大。P(?3,4)?直线l的方程为3(x+3)?4(y?4)=0.即3x?4y+25=0.(3)到两点A(2,6)、B(?4,?2)距离相等;P(?3,4)??A(2,6)B(?4,?2)?解:(1)直线l与AB平行,即4x?3y+24=0(2)直线l过AB的中点,AB的中点坐标为(?1,2),即x+y?1=0(4)直线l与x轴负半轴、y轴正半轴围成直角三角形,且使三角形的面积最小。P(?3,4)?AB解:设直线方程为y?4=k(x+3)(k>0)斜率k存在三、课堂练习已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:
(1)过定点A(?3,4);(2)斜率为 .分析:选择适当的直线方程的形式。解:设直线方程为y?4=k(x+3),BB(0,3k+4)令x=0,得y=3k+4,令y=0,得x= ,C|9k2+24k+16|=6|k|,(2)设直线方程的形式为 ,?b=?1.直线方程的形式为 ,4.注重数形结合、分类讨论思想的运用.四、课堂小结1.求直线方程需要两个独立的条件.2.求直线方程的方法:①直接法;②待定系数法.3.注意各种直线方程的适用范围,求解时要防止可能产生的遗漏情况.
斜率 (倾斜角不是直角)。这便是直线的点方向式、点法向式、点斜式
的由来,斜截式是点斜式的特例。直线过定点方程ax+by+c=0(a,b不全为0)叫做直线方程的一般式,任何一条直线的方程都可以化成一般式。问题2 直线的一般式方程问题2:直线方程归纳点P(x0,y0)和方向向量(u,v)不垂直于
x、y轴的直线点P(x0,y0)和法向量(a,b)任意直线点P(x0,y0)
和斜率ky?y0=k(x?x0)不垂直于
x轴的直线斜率k和在y轴上的截距by=kx+b不垂直于
x轴的直线两个独立的条件ax+by+c=0a,b不全为0二、应用举例例:已知直线l过点P(?3,4),求满足下列条件的直线l的方程:(1)过另一点Q(a,1);P(?3,4)?1解:当a=?3时,l:x=?3;当a??3时,直线l的法向量为(3,a+3),直线l的方程为3(x+3)+(a+3)(y?4)=0.(2)坐标原点O到直线l的距离最大;分析:当OP与直线l垂直时,点O
到直线l的距离最大。P(?3,4)?直线l的方程为3(x+3)?4(y?4)=0.即3x?4y+25=0.(3)到两点A(2,6)、B(?4,?2)距离相等;P(?3,4)??A(2,6)B(?4,?2)?解:(1)直线l与AB平行,即4x?3y+24=0(2)直线l过AB的中点,AB的中点坐标为(?1,2),即x+y?1=0(4)直线l与x轴负半轴、y轴正半轴围成直角三角形,且使三角形的面积最小。P(?3,4)?AB解:设直线方程为y?4=k(x+3)(k>0)斜率k存在三、课堂练习已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:
(1)过定点A(?3,4);(2)斜率为 .分析:选择适当的直线方程的形式。解:设直线方程为y?4=k(x+3),BB(0,3k+4)令x=0,得y=3k+4,令y=0,得x= ,C|9k2+24k+16|=6|k|,(2)设直线方程的形式为 ,?b=?1.直线方程的形式为 ,4.注重数形结合、分类讨论思想的运用.四、课堂小结1.求直线方程需要两个独立的条件.2.求直线方程的方法:①直接法;②待定系数法.3.注意各种直线方程的适用范围,求解时要防止可能产生的遗漏情况.
