11.3 解二元一次方程组

课件17张PPT。
解二元一次方程组(2)问题2：代入消元法解二元一次方程组 的一般步骤是什么?回顾与思考问题1:解方程组的基本思路是什么？把“二元”变为“一元”选择组中适当的一个方程，变形
代入另一个方程消元，化二元为一元
解这个一元一次方程，得到一个未知数
将它代回原方程，求另一个未知数
用大括号联立　“解”
检验（在草稿纸上进行）
具体步骤列方程组为｛3x+2y=235x+2y=33考考你（1）3瓶苹果汁的售价+ 2瓶橙汁的售价=23（2）5瓶苹果汁的售价+ 2瓶橙汁的售价=33解:设每瓶苹果汁是x元每瓶橙汁售价是y元.
分析:买3瓶苹果汁和2瓶橙汁共需23元,买5瓶苹果汁和2瓶橙汁共需33元,每瓶苹果汁和每瓶橙汁售价各是多少?
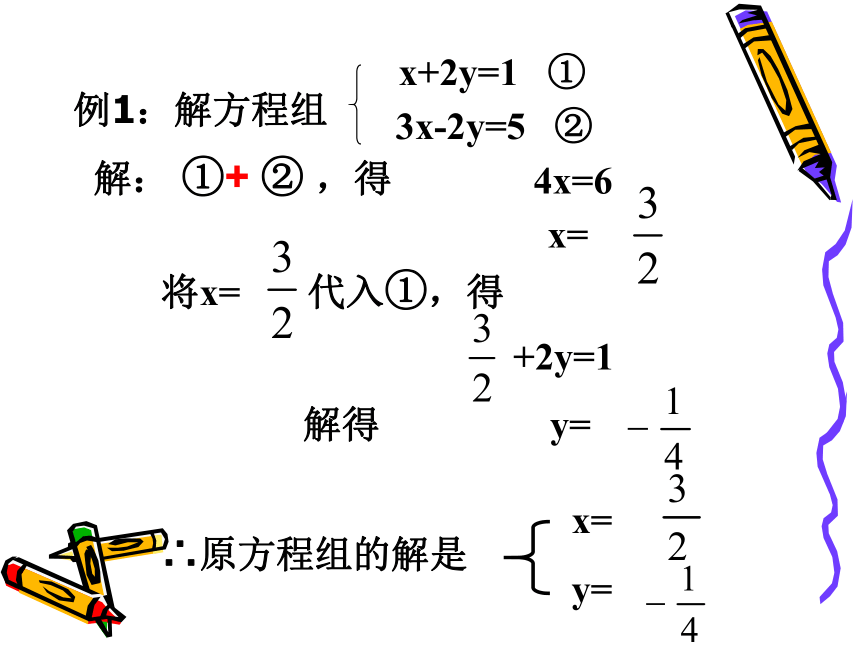
3x+2y=235x+2y=33｛②①解： ②－ ①,得2x=10x=5把x=5代入①,得3×5+2y=23解得y=4∴原方程组的解是｛x=5y=4解： ①+ ② ，得 　 x=　将x= 代入①，得+2y=1 解得 y=4x=6
2x+y=32 ① 2x-y=0 ② 1.2.7x+3y=11 ① 2x - 3y=7 ② 看看你掌握了吗？练习：解下列方程组解： ②－ ①,得解： ①+ ② ，得 ①当相同字母的未知数的系数相同时;②当相同字母的未知数的系数互为相反数时;③当相同字母的未知数的系数不相等时.反思:解： ①×3, 得 15x-6y=12 ③
②×2，得 4x-6y=-10 ④
③-④，得 11 x=22
解得 x=2
将x=2 代入①，得 5×2-2y=4
解得 y=3
　　∴原方程组的解是例2：解方程组 5x-2y=4 ① 2x-3y=-5 ② 本题中消去了y,变成了只含有x的一次方程.
可以先消去x吗?怎么做?　　上面解方程组的基本思路还是“消元”------把“二元”变为“一元”。
主要步骤是：把方程组的两个方程（或先作适当变形）相加或相减，消去其中一个未知数，把解二元一次方程组转化为解一元一次方程.这种解方程组的方法叫做加减消元法，简称加减法．同学们：你从上面的学习中体会到解方程组的基本思路是什么吗？主要步骤有哪些吗？你有几种方法解这个方程组?动手试一试想一想：加减消元法和代入消元法有什么异同?这节课，我的收获是--- 1、 本节课我们知道了用加减消元法解二元一次方程组的基本思路是“消元”。即把“二元”化为“一元”，化二元一次方程组为一元一次方程。
2、用加减消元法解二元一次方程组的一般步骤.
3、把求出的解代入原方程组，可以检验解是否正确。
相信你能行1.2.1、解二元一次方程组⑵ 6x+5y=25 ① 3x +4y=20 ② (4) 2x+3y=-1 ① 4x -9y=8 ② 练一练