2.2.1对数与对数运算(带解析)
文档属性
| 名称 | 2.2.1对数与对数运算(带解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 493.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-14 00:00:00 | ||
图片预览

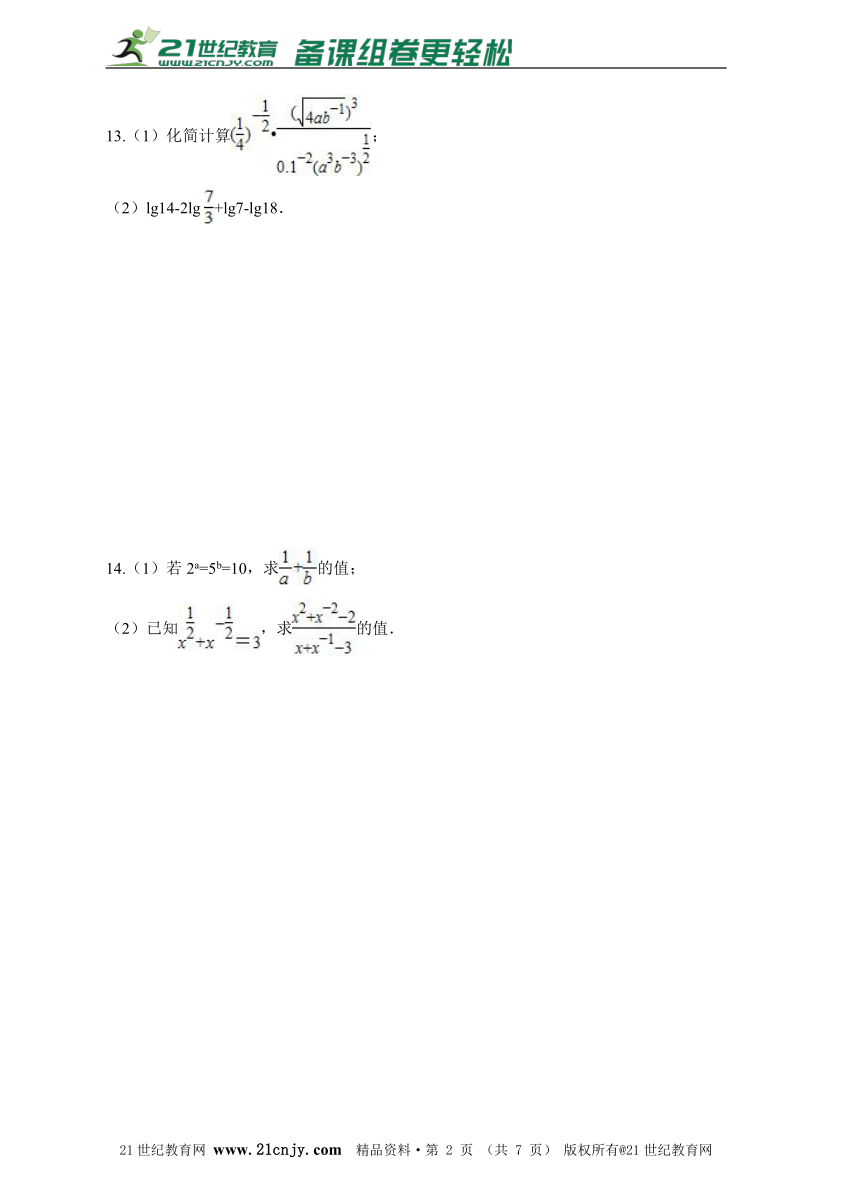
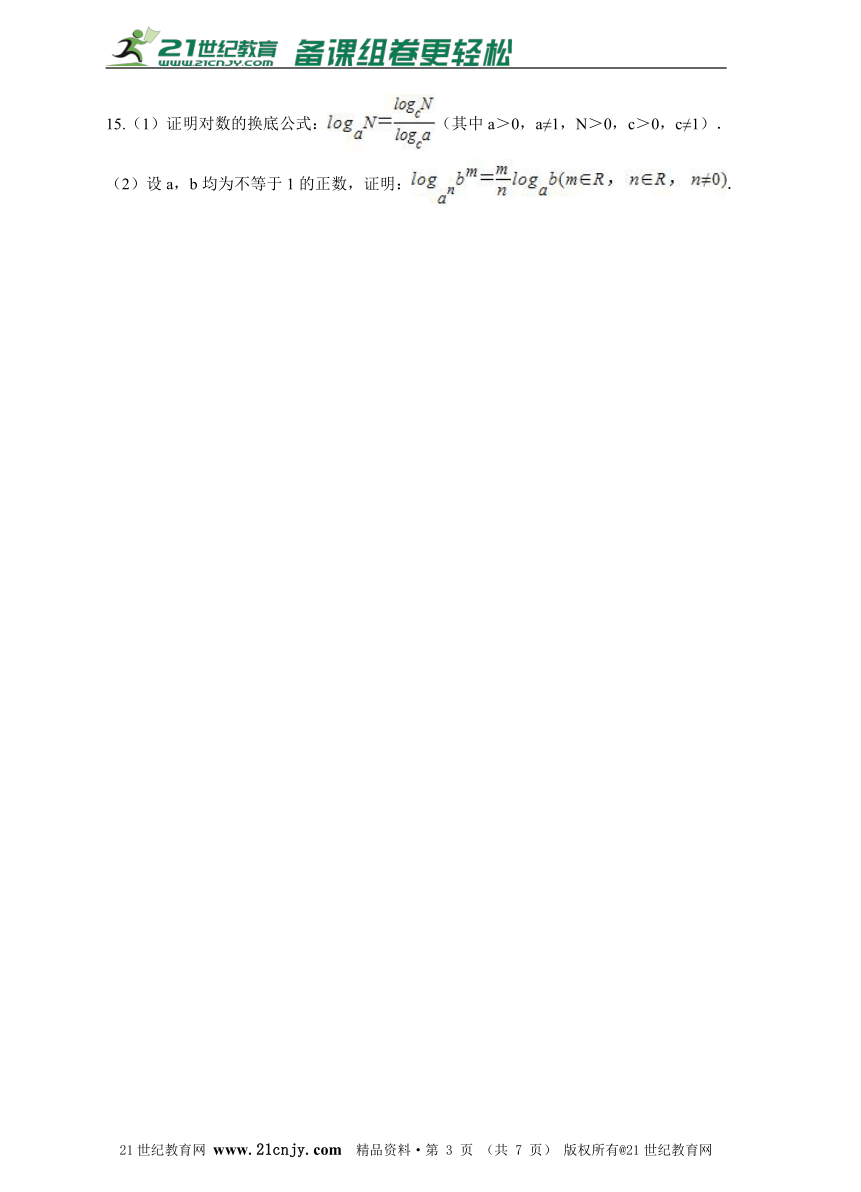
文档简介
2.2.1对数与对数运算(带解析)
一、选择题
1.的值是( )
A. B.1 C. D.2
2.若log2=1,则x的值是( )
A.2 B.4 C.6 D.9
3.已知2x=,log23=y,则2x+2y的值为( )
A. B. C.54 D.
4.(log29)?(log34)=( )
A. B. C.2 D.4
5.已知ln2=a,ln3=b,那么log32用含a,b的代数式表示为( )
A.a+b B.a-b C.ab D.
6.设a=log32,b=ln2,c=,则( )
A.a<b<c B.b<c<a C.c<a<b D.c<b<a
7.已知,则f(2012)=( )
A.81 B.9 C.3 D.
8.下列等式中一定正确的是( )
A. B. C. D.
二、填空题
9.(lg5)2+lg2×lg50=?? ? .
10.已知log147=a,14b=5,用a,b表示log3570?? ? .
11.已知f(x3)=logax,且f(8)=1,则a=? ?? .21教育网
12.设f(x)=logax(a>0且a≠1),若f(x1)+f(x2)+…+f(xn)=1(x∈R+,i=1,2…n),则f(x13)+f(x23)+…+f(xn3)的值等于??? .www.21-cn-jy.com
三、解答题
13.(1)化简计算; (2)lg14-2lg?+lg7-lg18.
14.(1)若2a=5b=10,求的值; (2)已知,求的值.
15.(1)证明对数的换底公式:(其中a>0,a≠1,N>0,c>0,c≠1). (2)设a,b均为不等于1的正数,证明:.
参考答案及解析
1.A
【解析】根据,从而得到答案. . 2.D
5.D
【解析】由已知中In2=a,In3=b,用换底公式可将log32化用自然对数表示的形式,代入In2=a,In3=b,即可得到答案. ∵In2=a,In3=b, 又∵log32= ∴log32= 6.C21世纪教育网版权所有
【解析】根据a的真数与b的真数相等可取倒数,使底化相同,找中间量1与之比较大小,便值a、b、c的大小关系. a=log32=,b=ln2=, 而log23>log2e>1,所以a<b, c==,而, 所以c<a,综上c<a<b, 7.B21cnjy.com
【解析】利用分段函数在不同区间内的解析式不同即可计算出函数值. ∵x>5时,f(x)=f(x-2), ∴f(2012)=f(2×1003+6)=f(2×1003+6-2)=f(4), 21·cn·jy·com
D.=loga|x|≠logax.(x≠1) 9.1.
【解析】由式子的特点把50拆成5与10的乘积,则lg50=lg10+lg5,再利用lg5+lg2=1进行化简求值. (lg5)2+lg2×lg50 =(lg5)2+lg2×(lg10+lg5) =(lg5)2+lg2+(lg5)(lg2) =lg5(lg5+lg2)+lg2=1. 10.2·1·c·n·j·y
【解析】由题意知,将b表示出来,得b=log145再对log3570用换底公式,用a,b表示log3570 由14b=5得b=log145,又log147=a log3570= 11.2.【来源:21·世纪·教育·网】
【解析】先变形符合已知条件即可求出. 由x3=8,解得x=2, ∴f(8)=f(23)=loga2=1,化为a1=2,解得a=2. 12.321·世纪*教育网
【解析】由对数的运算性质可得f(x1)+f(x2)+…+f(xn)=1?f(x1)+f(x2)+…+f(xn)www-2-1-cnjy-com
(1)原式===; (2)原式=lg14-lg+lg7-lg18=lg=lg1=0. 14.(1)12-1-c-n-j-y
(2)
【解析】(1)要求的值需求出a,b的值故可根据条件2a=5b=10结合指数式与对数式的转化公式:ab=N?b=logaN求出a,b然后代入再结合换底公式化简即可得解. (2)通过已知表达式求出x+x-1,x2+x-2的值,然后求解所求表达式的值即可. (1)∵2a=5b=10 ∴a=log210,b=log510 ∴==log102+log105=log1010=1. (2)因为,所以, ∴x+2+x-1=9, ∴x+x-1=7, ∴(x+x-1)2=49, ∴x2+x-2=47 ∴==. 15.见解析 21*cnjy*com
【解析】(1)设logaN=b,则ab=N,两端同时取以c为底的对数,整理即可证得结论;
∴==logab.
一、选择题
1.的值是( )
A. B.1 C. D.2
2.若log2=1,则x的值是( )
A.2 B.4 C.6 D.9
3.已知2x=,log23=y,则2x+2y的值为( )
A. B. C.54 D.
4.(log29)?(log34)=( )
A. B. C.2 D.4
5.已知ln2=a,ln3=b,那么log32用含a,b的代数式表示为( )
A.a+b B.a-b C.ab D.
6.设a=log32,b=ln2,c=,则( )
A.a<b<c B.b<c<a C.c<a<b D.c<b<a
7.已知,则f(2012)=( )
A.81 B.9 C.3 D.
8.下列等式中一定正确的是( )
A. B. C. D.
二、填空题
9.(lg5)2+lg2×lg50=?? ? .
10.已知log147=a,14b=5,用a,b表示log3570?? ? .
11.已知f(x3)=logax,且f(8)=1,则a=? ?? .21教育网
12.设f(x)=logax(a>0且a≠1),若f(x1)+f(x2)+…+f(xn)=1(x∈R+,i=1,2…n),则f(x13)+f(x23)+…+f(xn3)的值等于??? .www.21-cn-jy.com
三、解答题
13.(1)化简计算; (2)lg14-2lg?+lg7-lg18.
14.(1)若2a=5b=10,求的值; (2)已知,求的值.
15.(1)证明对数的换底公式:(其中a>0,a≠1,N>0,c>0,c≠1). (2)设a,b均为不等于1的正数,证明:.
参考答案及解析
1.A
【解析】根据,从而得到答案. . 2.D
5.D
【解析】由已知中In2=a,In3=b,用换底公式可将log32化用自然对数表示的形式,代入In2=a,In3=b,即可得到答案. ∵In2=a,In3=b, 又∵log32= ∴log32= 6.C21世纪教育网版权所有
【解析】根据a的真数与b的真数相等可取倒数,使底化相同,找中间量1与之比较大小,便值a、b、c的大小关系. a=log32=,b=ln2=, 而log23>log2e>1,所以a<b, c==,而, 所以c<a,综上c<a<b, 7.B21cnjy.com
【解析】利用分段函数在不同区间内的解析式不同即可计算出函数值. ∵x>5时,f(x)=f(x-2), ∴f(2012)=f(2×1003+6)=f(2×1003+6-2)=f(4), 21·cn·jy·com
D.=loga|x|≠logax.(x≠1) 9.1.
【解析】由式子的特点把50拆成5与10的乘积,则lg50=lg10+lg5,再利用lg5+lg2=1进行化简求值. (lg5)2+lg2×lg50 =(lg5)2+lg2×(lg10+lg5) =(lg5)2+lg2+(lg5)(lg2) =lg5(lg5+lg2)+lg2=1. 10.2·1·c·n·j·y
【解析】由题意知,将b表示出来,得b=log145再对log3570用换底公式,用a,b表示log3570 由14b=5得b=log145,又log147=a log3570= 11.2.【来源:21·世纪·教育·网】
【解析】先变形符合已知条件即可求出. 由x3=8,解得x=2, ∴f(8)=f(23)=loga2=1,化为a1=2,解得a=2. 12.321·世纪*教育网
【解析】由对数的运算性质可得f(x1)+f(x2)+…+f(xn)=1?f(x1)+f(x2)+…+f(xn)www-2-1-cnjy-com
(1)原式===; (2)原式=lg14-lg+lg7-lg18=lg=lg1=0. 14.(1)12-1-c-n-j-y
(2)
【解析】(1)要求的值需求出a,b的值故可根据条件2a=5b=10结合指数式与对数式的转化公式:ab=N?b=logaN求出a,b然后代入再结合换底公式化简即可得解. (2)通过已知表达式求出x+x-1,x2+x-2的值,然后求解所求表达式的值即可. (1)∵2a=5b=10 ∴a=log210,b=log510 ∴==log102+log105=log1010=1. (2)因为,所以, ∴x+2+x-1=9, ∴x+x-1=7, ∴(x+x-1)2=49, ∴x2+x-2=47 ∴==. 15.见解析 21*cnjy*com
【解析】(1)设logaN=b,则ab=N,两端同时取以c为底的对数,整理即可证得结论;
∴==logab.
