2.2对数函数节综合检测题(带解析)
文档属性
| 名称 | 2.2对数函数节综合检测题(带解析) |  | |
| 格式 | zip | ||
| 文件大小 | 652.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-14 10:20:26 | ||
图片预览




文档简介
2.2对数函数节综合检测题(带解析)
一、选择题
1.下列说法中,正确的是( )
A.对任意x∈R,都有3x>2x B.y=()-x是R上的增函数; C.若x∈R且x≠0,则log2x2=2log2 D.在同一坐标系中,y=2x与y=log2x的图象关于直线y=x对称www-2-1-cnjy-com
2.a=log0.50.6,b=,c=,则( )
A.a<b<c B.b<a<c C.a<c<b D.c<a<b
3.设lg2=a,lg3=b,则log512等于( )
A. B. C. D.
4.函数的定义域是?( )
A. B. C. D.
5.函数y=的值域是( )
A.R B.[8,+∞) C.(-∞,-3] D.[3,+∞)
6.函数f(x)=loga|x+1|,在(-1,0)上有f(x)>0,那么( )
A.f(x)在(-∞,0)上是增函数 B.f(x)在(-∞,0)上是减函数 C.f(x)在(-∞,-1)上是增函数 D.f(x)在(-∞,-0)上是减函数【出处:21教育名师】
7.若函数f(x)=loga(2x2+x)(a>0,a≠1)在区间(0,)内恒有f(x)>0,则f(x)的单调递增区间是( )21教育网
A.(-∞,-) B. C. D.(0,+∞)
8.函数y=log2x与的图象( )
A.关于原点对称 B.关于x轴对称 C.关于y轴对称 D.关于y=x对称
9.如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”.在下面的五个点M(1,1),N(1,2),P(2,1),Q(2,2),G(2,0.5)中,“好点”的个数为( )
A.0个 B.1个 C.2个 D.3个
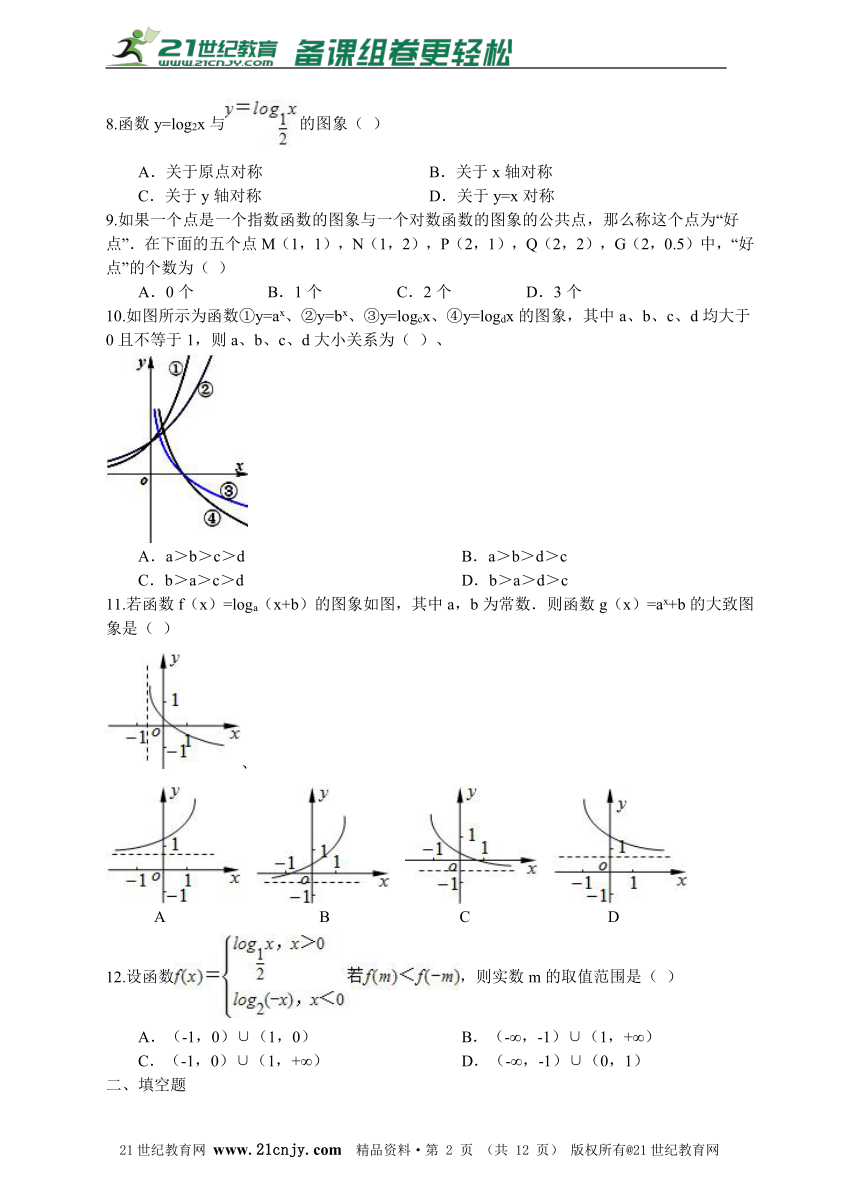
10.如图所示为函数①y=ax、②y=bx、③y=logcx、④y=logdx的图象,其中a、b、c、d均大于0且不等于1,则?a、b、c、d大小关系为( )、
A.a>b>c>d B.a>b>d>c C.b>a>c>d D.b>a>d>c
11.若函数f(x)=loga(x+b)的图象如图,其中a,b为常数.则函数g(x)=ax+b的大致图象是( )21教育名师原创作品
、
A B C D
12.设函数,则实数m的取值范围是( )
A.(-1,0)∪(1,0) B.(-∞,-1)∪(1,+∞) C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1)
二、填空题
13.设,则a,b,c的大小关系为??? .
14.设2a=5b=m,且,m=??? .
15.函数的定义域是??? .
16.函数的单调增区间是?? ? ,值域为??? .
17.函数,且a≠1)的图象恒过定点M,则M的坐标为??? .
18.下列说法正确的是??? .(只填正确说法序号) ①若集合A={y|y=x-1},B={y|y=x2-1},则A∩B={(0,-1),(1,0)}; ②是函数解析式; ③若函数f(x)在(-∞,0],[0,+∞)都是单调增函数,则f(x)在(-∞,+∞)上也是增函数; ④是非奇非偶函数; ⑤函数的单调增区间是(-∞,1).2·1·c·n·j·y
三、解答题
19.(1)计算的值。
(2)已知用a,b表示
20.已知函数 (1)若,求函数f(x)最大值和最小值; (2)若方程f(x)+m=0有两根α,β,试求α?β的值.21·cn·jy·com
21.(1)如果定义在区间(-1,0)的函数f(x)=log3a(x+1)满足f(x)<0,求a的取值范围; (2)解方程:.21世纪教育网版权所有
22.已知常数a>0且a≠1,变数x、y满足?3logxa+logax-logxy=3 (1)若x=at(t≠0),试以a、t表示y. (2)若t∈{t|t2-4t+3≤0}时,y有最小值8,求a和x的值.21cnjy.com
参考答案及解析
1.D
【解析】由x<0,判断A和C不成立;由y=()-x是R上的减函数,判断B不成立;指数函数和对数函数互为反函数,故D成立. 当x<0时,3x<2x,故A不成立; y=()-x=是R上的减函数,故B不成立; 21·世纪*教育网
4.A
【解析】函数的定义域是:,由此能求出结果. 函数的定义域是:,解得, 5.C
【解析】此为一复合函数,要由里往外求,先求内层函数x2-6x+17,用配方法求即可,再求复合函数的值域. ∵t=x2-6x+17=(x-3)2+8≥8 ∴内层函数的值域变[8,+∞) ??y=在[8,+∞)是减函数, 故y≤=-3 ∴函数y=的值域是(-∞,-3] 6.C2-1-c-n-j-y
【解析】函数f(x)=loga|x+1|,在(-1,0)上有f(x)>0,可得出对数函数的底数a∈(0,1),由此知外层函数是减函数,由此关系对四个选项进行判断选出正确选项即可 由题意f(x)=loga|x+1|,在(-1,0)上有f(x)>0,可得a∈(0,1),由此知y=loga x是一个减函数 A选项不正确,因为x∈(-∞,0)时,内层函数|x+1|不是一个单调函数,故不能得出f(x)在(-∞,0)上是增函数, B选项不正确,因为x∈(-∞,0)时,内层函数|x+1|不是一个单调函数,故不能得出f(x)在(-∞,0)上是减函数, C选项正确,因为x∈(-∞,-1)时,内层函数|x+1|是一个单调减函数,故能得出f(x)在(-∞,
8.B
【解析】由==-log2x,知-y=log2x,故函数y=log2x与的图象关于x轴对称. ∵==-log2x, 即-y=log2x, ∴函数y=log2x与的图象关于x轴对称, 9.C 21*cnjy*com
【解析】利用对数函数的性质,易得M,N不是好点,利用指数函数的性质,易得N,P不是好点,利用“好点”的定义,我们易构造指数方程和对数方程,得到Q(2,2),G(2,0.5)两个点是好点,从而得到答案. 当X=1时,对数函数y=logax(a>0,a≠1)恒过(1,0)点, 故M(1,1),N(1,2),一定不是好点, 当Y=1时,指数函数y=ax(a>0,a≠1)恒过(0,1)点, 故P(2,1)也一定不是好点, 而Q(2,2)是函数y=与y=的交点; G(2,0.5)是函数y=与y=log4x的交点; 故好点有2个, 10.B【来源:21cnj*y.co*m】
【解析】根据①和②都是增函数,作出直线x=1和函数①②图象的交点,可得a>b,故a>b>1.根据函数③和函数④是减函数,作出直线y=1和函数③④图象的交点,可得d>c,故【版权所有:21教育】
①当m<0时,f(m)=log2(-m)且 ∵f(m)<f(-m), ∴log2(-m)<,即log2(-m)<, 也就是-m<-,解之得-1<m<0; ②当m>0时,f(m)=且f(-m)=log2m ∵f(m)<f(-m), ∴<log2m,即<log2, 也就是m>,解之得m>1 综上所述,实数m的取值范围是-1<m<0或m>1 13.b<c<a.【来源:21·世纪·教育·网】
【解析】直接判断a、b、c的范围,然后半径大小即可. 因为, 所以b<c<a. 14.
【解析】先解出a,b,再代入方程利用换底公式及对数运算性质化简即可得到m的等式,求m.
∵t≤4,∴y≥-2,∴函数的值域为[-2,+∞) 17.(2,3)
【解析】由对数的性质知,当真数为1时,对数值一定为0,由此性质求函数的定点即可. 令,得x=2. 把x=2代入,且a≠1), 得y=3+loga1=3, ∴函数,且a≠1)的图象恒过定点M(2,3). 18.④21*cnjy*com
【解析】由集合运算的封闭性知①不对;由x-3≥0且2-x≥0求出函数定义域是空集知②不对;因为函数的单调区间不能并在一起,可以举例加以理解知③不对;求出函数的定义域化简函数的解析式和奇偶函数的定义知④对;由x2-2x-3>0求出函数的定义域可判断⑤不对. ①因集合A、B是数集,则A∩B也是数集,故①不对; ②、由x-3≥0且2-x≥0解得,x∈?,则不满足函数的定义中两个非空数集,故②不对; ③、函数的单调区间不能并在一起,如y=-的增区间是(-∞,0),(0,+∞),而不是 (-∞,0)∪(0,+∞),故③不对;
所以log23?log37=log27=ab, 所以log1456== 20.(1)
(2)
【解析】(1)将f(x)计算化简得出f(x)=(log3x-3)(log3x+1),令log3x=t,转化为二次函数解决. (2)结合(1)即为方程(log3x)2-2log3x-3+m=0的两解为α,β,得出log3α+log3β=2,再求出α?β. (1)根据对数的运算性质得出 f(x)=(log3x-3)(log3x+1) 令log3x=t,t∈[-3,-2] 则g(t)=t2-2t-3,t∈[-3,-2] g(t)对称轴t=1www.21-cn-jy.com
经检验,1是原方程的解 ∴原方程的解为1
22.(1)y=
(2)a=16, x=64
【解析】(1)由题意利用换底公式可得 logay=-3logax+3,再由x=at(t≠0),可得 logax=t,由此可用a、t表示y. (2)由t2-4t+3≤0可得 1≤t≤3.分0<a<1和a>1两种情况,并根据y有最小值8,求得a的值,由此求得对应的x的值. (1)∵3logxa+logax-logxy=3,由换底公式可得 +logax-=3, 解得 logay=-3logax+3. 若x=at(t≠0),则 logax=t, ∴logay=t2-3t+3,∴y=. (2)由t2-4t+3≤0可得 1≤t≤3. 当0<a<1时,由于y有最小值8,故函数u=t2-3t+3=?必有最大值,故当 t=3时,函数u取得最大值为3,即 a3=8,a=2,这与0<a<1矛盾. 当a>1时,由于y有最小值8,故函数u=t2-3t+3= 必有最小值,故当 t=时,
函数u取得最小值为,即=8,a=16,此时x=64.
一、选择题
1.下列说法中,正确的是( )
A.对任意x∈R,都有3x>2x B.y=()-x是R上的增函数; C.若x∈R且x≠0,则log2x2=2log2 D.在同一坐标系中,y=2x与y=log2x的图象关于直线y=x对称www-2-1-cnjy-com
2.a=log0.50.6,b=,c=,则( )
A.a<b<c B.b<a<c C.a<c<b D.c<a<b
3.设lg2=a,lg3=b,则log512等于( )
A. B. C. D.
4.函数的定义域是?( )
A. B. C. D.
5.函数y=的值域是( )
A.R B.[8,+∞) C.(-∞,-3] D.[3,+∞)
6.函数f(x)=loga|x+1|,在(-1,0)上有f(x)>0,那么( )
A.f(x)在(-∞,0)上是增函数 B.f(x)在(-∞,0)上是减函数 C.f(x)在(-∞,-1)上是增函数 D.f(x)在(-∞,-0)上是减函数【出处:21教育名师】
7.若函数f(x)=loga(2x2+x)(a>0,a≠1)在区间(0,)内恒有f(x)>0,则f(x)的单调递增区间是( )21教育网
A.(-∞,-) B. C. D.(0,+∞)
8.函数y=log2x与的图象( )
A.关于原点对称 B.关于x轴对称 C.关于y轴对称 D.关于y=x对称
9.如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”.在下面的五个点M(1,1),N(1,2),P(2,1),Q(2,2),G(2,0.5)中,“好点”的个数为( )
A.0个 B.1个 C.2个 D.3个
10.如图所示为函数①y=ax、②y=bx、③y=logcx、④y=logdx的图象,其中a、b、c、d均大于0且不等于1,则?a、b、c、d大小关系为( )、
A.a>b>c>d B.a>b>d>c C.b>a>c>d D.b>a>d>c
11.若函数f(x)=loga(x+b)的图象如图,其中a,b为常数.则函数g(x)=ax+b的大致图象是( )21教育名师原创作品
、
A B C D
12.设函数,则实数m的取值范围是( )
A.(-1,0)∪(1,0) B.(-∞,-1)∪(1,+∞) C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1)
二、填空题
13.设,则a,b,c的大小关系为??? .
14.设2a=5b=m,且,m=??? .
15.函数的定义域是??? .
16.函数的单调增区间是?? ? ,值域为??? .
17.函数,且a≠1)的图象恒过定点M,则M的坐标为??? .
18.下列说法正确的是??? .(只填正确说法序号) ①若集合A={y|y=x-1},B={y|y=x2-1},则A∩B={(0,-1),(1,0)}; ②是函数解析式; ③若函数f(x)在(-∞,0],[0,+∞)都是单调增函数,则f(x)在(-∞,+∞)上也是增函数; ④是非奇非偶函数; ⑤函数的单调增区间是(-∞,1).2·1·c·n·j·y
三、解答题
19.(1)计算的值。
(2)已知用a,b表示
20.已知函数 (1)若,求函数f(x)最大值和最小值; (2)若方程f(x)+m=0有两根α,β,试求α?β的值.21·cn·jy·com
21.(1)如果定义在区间(-1,0)的函数f(x)=log3a(x+1)满足f(x)<0,求a的取值范围; (2)解方程:.21世纪教育网版权所有
22.已知常数a>0且a≠1,变数x、y满足?3logxa+logax-logxy=3 (1)若x=at(t≠0),试以a、t表示y. (2)若t∈{t|t2-4t+3≤0}时,y有最小值8,求a和x的值.21cnjy.com
参考答案及解析
1.D
【解析】由x<0,判断A和C不成立;由y=()-x是R上的减函数,判断B不成立;指数函数和对数函数互为反函数,故D成立. 当x<0时,3x<2x,故A不成立; y=()-x=是R上的减函数,故B不成立; 21·世纪*教育网
4.A
【解析】函数的定义域是:,由此能求出结果. 函数的定义域是:,解得, 5.C
【解析】此为一复合函数,要由里往外求,先求内层函数x2-6x+17,用配方法求即可,再求复合函数的值域. ∵t=x2-6x+17=(x-3)2+8≥8 ∴内层函数的值域变[8,+∞) ??y=在[8,+∞)是减函数, 故y≤=-3 ∴函数y=的值域是(-∞,-3] 6.C2-1-c-n-j-y
【解析】函数f(x)=loga|x+1|,在(-1,0)上有f(x)>0,可得出对数函数的底数a∈(0,1),由此知外层函数是减函数,由此关系对四个选项进行判断选出正确选项即可 由题意f(x)=loga|x+1|,在(-1,0)上有f(x)>0,可得a∈(0,1),由此知y=loga x是一个减函数 A选项不正确,因为x∈(-∞,0)时,内层函数|x+1|不是一个单调函数,故不能得出f(x)在(-∞,0)上是增函数, B选项不正确,因为x∈(-∞,0)时,内层函数|x+1|不是一个单调函数,故不能得出f(x)在(-∞,0)上是减函数, C选项正确,因为x∈(-∞,-1)时,内层函数|x+1|是一个单调减函数,故能得出f(x)在(-∞,
8.B
【解析】由==-log2x,知-y=log2x,故函数y=log2x与的图象关于x轴对称. ∵==-log2x, 即-y=log2x, ∴函数y=log2x与的图象关于x轴对称, 9.C 21*cnjy*com
【解析】利用对数函数的性质,易得M,N不是好点,利用指数函数的性质,易得N,P不是好点,利用“好点”的定义,我们易构造指数方程和对数方程,得到Q(2,2),G(2,0.5)两个点是好点,从而得到答案. 当X=1时,对数函数y=logax(a>0,a≠1)恒过(1,0)点, 故M(1,1),N(1,2),一定不是好点, 当Y=1时,指数函数y=ax(a>0,a≠1)恒过(0,1)点, 故P(2,1)也一定不是好点, 而Q(2,2)是函数y=与y=的交点; G(2,0.5)是函数y=与y=log4x的交点; 故好点有2个, 10.B【来源:21cnj*y.co*m】
【解析】根据①和②都是增函数,作出直线x=1和函数①②图象的交点,可得a>b,故a>b>1.根据函数③和函数④是减函数,作出直线y=1和函数③④图象的交点,可得d>c,故【版权所有:21教育】
①当m<0时,f(m)=log2(-m)且 ∵f(m)<f(-m), ∴log2(-m)<,即log2(-m)<, 也就是-m<-,解之得-1<m<0; ②当m>0时,f(m)=且f(-m)=log2m ∵f(m)<f(-m), ∴<log2m,即<log2, 也就是m>,解之得m>1 综上所述,实数m的取值范围是-1<m<0或m>1 13.b<c<a.【来源:21·世纪·教育·网】
【解析】直接判断a、b、c的范围,然后半径大小即可. 因为, 所以b<c<a. 14.
【解析】先解出a,b,再代入方程利用换底公式及对数运算性质化简即可得到m的等式,求m.
∵t≤4,∴y≥-2,∴函数的值域为[-2,+∞) 17.(2,3)
【解析】由对数的性质知,当真数为1时,对数值一定为0,由此性质求函数的定点即可. 令,得x=2. 把x=2代入,且a≠1), 得y=3+loga1=3, ∴函数,且a≠1)的图象恒过定点M(2,3). 18.④21*cnjy*com
【解析】由集合运算的封闭性知①不对;由x-3≥0且2-x≥0求出函数定义域是空集知②不对;因为函数的单调区间不能并在一起,可以举例加以理解知③不对;求出函数的定义域化简函数的解析式和奇偶函数的定义知④对;由x2-2x-3>0求出函数的定义域可判断⑤不对. ①因集合A、B是数集,则A∩B也是数集,故①不对; ②、由x-3≥0且2-x≥0解得,x∈?,则不满足函数的定义中两个非空数集,故②不对; ③、函数的单调区间不能并在一起,如y=-的增区间是(-∞,0),(0,+∞),而不是 (-∞,0)∪(0,+∞),故③不对;
所以log23?log37=log27=ab, 所以log1456== 20.(1)
(2)
【解析】(1)将f(x)计算化简得出f(x)=(log3x-3)(log3x+1),令log3x=t,转化为二次函数解决. (2)结合(1)即为方程(log3x)2-2log3x-3+m=0的两解为α,β,得出log3α+log3β=2,再求出α?β. (1)根据对数的运算性质得出 f(x)=(log3x-3)(log3x+1) 令log3x=t,t∈[-3,-2] 则g(t)=t2-2t-3,t∈[-3,-2] g(t)对称轴t=1www.21-cn-jy.com
经检验,1是原方程的解 ∴原方程的解为1
22.(1)y=
(2)a=16, x=64
【解析】(1)由题意利用换底公式可得 logay=-3logax+3,再由x=at(t≠0),可得 logax=t,由此可用a、t表示y. (2)由t2-4t+3≤0可得 1≤t≤3.分0<a<1和a>1两种情况,并根据y有最小值8,求得a的值,由此求得对应的x的值. (1)∵3logxa+logax-logxy=3,由换底公式可得 +logax-=3, 解得 logay=-3logax+3. 若x=at(t≠0),则 logax=t, ∴logay=t2-3t+3,∴y=. (2)由t2-4t+3≤0可得 1≤t≤3. 当0<a<1时,由于y有最小值8,故函数u=t2-3t+3=?必有最大值,故当 t=3时,函数u取得最大值为3,即 a3=8,a=2,这与0<a<1矛盾. 当a>1时,由于y有最小值8,故函数u=t2-3t+3= 必有最小值,故当 t=时,
函数u取得最小值为,即=8,a=16,此时x=64.
