26.1.2反比例函数的图象和性质(第1课时)导学案
文档属性
| 名称 | 26.1.2反比例函数的图象和性质(第1课时)导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 118.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 00:00:00 | ||
图片预览

文档简介
26.1.2
反比例函数的图象和性质
第1课时
反比例函数的图象和性质
1.会画出反比例函数的图象.
2.并能说出它的性质.
自学指导:阅读课本P4-6,完成下列问题.
知识探究
1.一次函数的表达式是:y=kx+b,它的图象是一条直线.
2.一次函数y=kx+b当k>0时,y随x的增大而增大.当k<0时,y随x的增大而减小.
3.作函数图象的一般步骤是:列表、描点、连线.
自学反馈
1.反比例函数的表达式是:
.
2.类比一次函数的作图象法,作反比例函数的图象的一般步骤也是:
、
、
.
3.反比例函数图象是
.
4.在反比例函数y=(k≠0,k为常数)中,当k>0时,双曲线位于
象限;当k<0时,双曲线位于
象限.
活动1
小组讨论
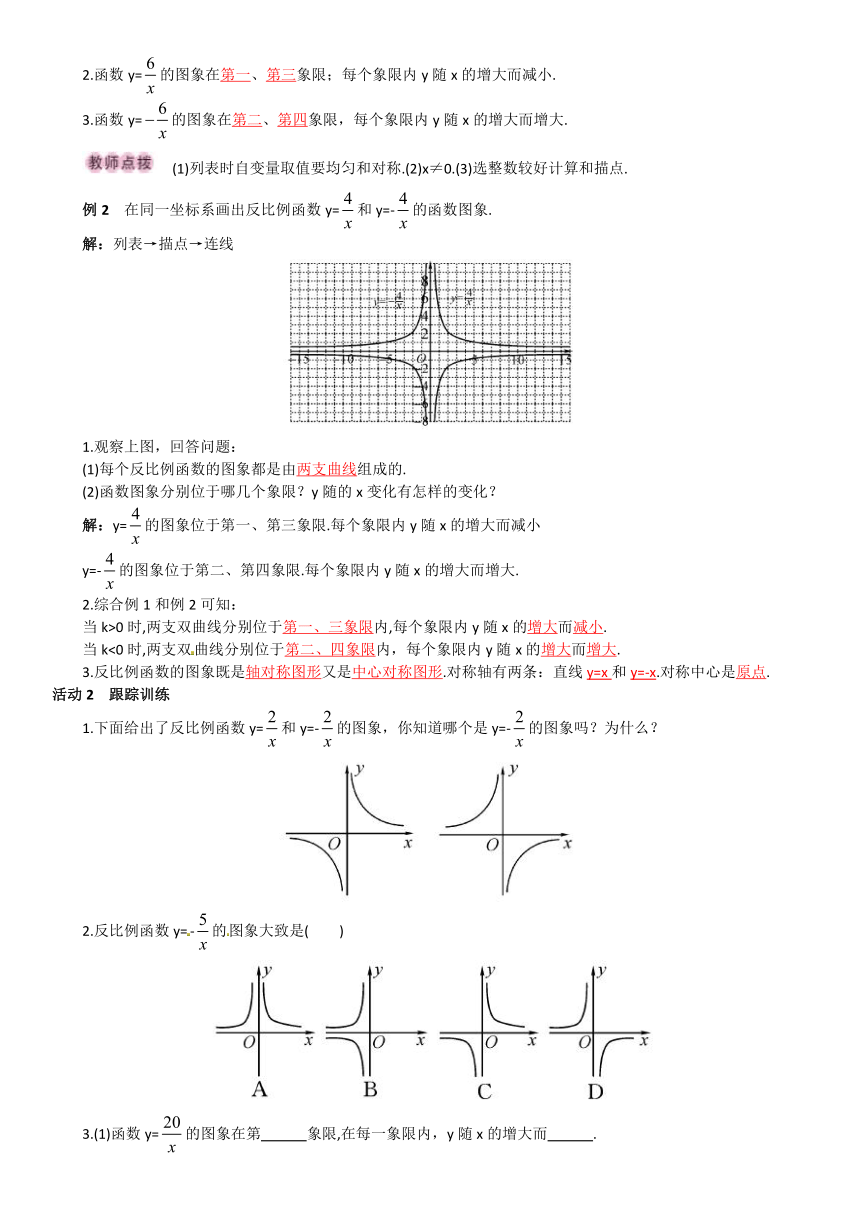
例1
画出反比例函数y=和y=的函数图象.
解:函数图象画法→描点法:列表→描点→连线
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
y=
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
y=
…
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
…
自学反馈
1.作反比例函数图象时应注意哪些问题?
列表时:自变量的值可以选取一些互为相反数的值,这样即可简化计算,又便于对称描点;
列表描点时:要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确的表达函数变化趋势;
连线时:一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性.
2.函数y=的图象在第一、第三象限;每个象限内y随x的增大而减小.
3.函数y=的图象在第二、第四象限,每个象限内y随x的增大而增大.
(1)列表时自变量取值要均匀和对称.(2)x≠0.(3)选整数较好计算和描点.
例2
在同一坐标系画出反比例函数y=和y=-的函数图象.
解:列表→描点→连线
1.观察上图,回答问题:
(1)每个反比例函数的图象都是由两支曲线组成的.
(2)函数图象分别位于哪几个象限?y随的x变化有怎样的变化?
解:y=的图象位于第一、第三象限.每个象限内y随x的增大而减小
y=-的图象位于第二、第四象限.每个象限内y随x的增大而增大.
2.综合例1和例2可知:
当k>0时,两支双曲线分别位于第一、三象限内,每个象限内y随x的增大而减小.
当k<0时,两支双曲线分别位于第二、四象限内,每个象限内y随x的增大而增大.
3.反比例函数的图象既是轴对称图形又是中心对称图形.对称轴有两条:直线y=x和y=-x.对称中心是原点.
活动2
跟踪训练
1.下面给出了反比例函数y=和y=-的图象,你知道哪个是y=-的图象吗?为什么?
2.反比例函数y=-的图象大致是(
)
3.(1)函数y=的图象在第
象限,在每一象限内,y随x的增大而
.
(2)函数y=-的图象在第
象限,在每一象限内,y随x的增大而
.
(3)函数y=,当x>0时,图象在第
象限,y随x的增大而
.
4.已知反比例函数y=.
(1)若函数的图象位于第一、三象限,则k
;
(2)若在每一象限内,y随x增大而增大,则k
.
5.函数y=kx-k与y=在同一直角坐标系中的图象可能是(
)
6.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是(
)
A.y=-5x-1
B.y=
C.y=-2x+2
D.y=4x
牢记函数图象的性质,严格按照函数图象性质判断.
课堂小结
反比例函数y=(k为常数,k≠0)的图象是双曲线;
当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小.
当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
1.y=(k≠0,k为常数)
2.列表
描点
连线
3.双曲线
4.第一、第三
第二、第四
【合作探究】
活动2
跟踪训练
1.第二个是y=-的图象.因为y=-中的k<0,图象在第二、四象限.
2.D
3.(1)一、三
减小
(2)二、四
增大
(3)一
减小
4.(1)<4
(2)>4
5.D
6.C
反比例函数的图象和性质
第1课时
反比例函数的图象和性质
1.会画出反比例函数的图象.
2.并能说出它的性质.
自学指导:阅读课本P4-6,完成下列问题.
知识探究
1.一次函数的表达式是:y=kx+b,它的图象是一条直线.
2.一次函数y=kx+b当k>0时,y随x的增大而增大.当k<0时,y随x的增大而减小.
3.作函数图象的一般步骤是:列表、描点、连线.
自学反馈
1.反比例函数的表达式是:
.
2.类比一次函数的作图象法,作反比例函数的图象的一般步骤也是:
、
、
.
3.反比例函数图象是
.
4.在反比例函数y=(k≠0,k为常数)中,当k>0时,双曲线位于
象限;当k<0时,双曲线位于
象限.
活动1
小组讨论
例1
画出反比例函数y=和y=的函数图象.
解:函数图象画法→描点法:列表→描点→连线
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
y=
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
y=
…
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
…
自学反馈
1.作反比例函数图象时应注意哪些问题?
列表时:自变量的值可以选取一些互为相反数的值,这样即可简化计算,又便于对称描点;
列表描点时:要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确的表达函数变化趋势;
连线时:一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性.
2.函数y=的图象在第一、第三象限;每个象限内y随x的增大而减小.
3.函数y=的图象在第二、第四象限,每个象限内y随x的增大而增大.
(1)列表时自变量取值要均匀和对称.(2)x≠0.(3)选整数较好计算和描点.
例2
在同一坐标系画出反比例函数y=和y=-的函数图象.
解:列表→描点→连线
1.观察上图,回答问题:
(1)每个反比例函数的图象都是由两支曲线组成的.
(2)函数图象分别位于哪几个象限?y随的x变化有怎样的变化?
解:y=的图象位于第一、第三象限.每个象限内y随x的增大而减小
y=-的图象位于第二、第四象限.每个象限内y随x的增大而增大.
2.综合例1和例2可知:
当k>0时,两支双曲线分别位于第一、三象限内,每个象限内y随x的增大而减小.
当k<0时,两支双曲线分别位于第二、四象限内,每个象限内y随x的增大而增大.
3.反比例函数的图象既是轴对称图形又是中心对称图形.对称轴有两条:直线y=x和y=-x.对称中心是原点.
活动2
跟踪训练
1.下面给出了反比例函数y=和y=-的图象,你知道哪个是y=-的图象吗?为什么?
2.反比例函数y=-的图象大致是(
)
3.(1)函数y=的图象在第
象限,在每一象限内,y随x的增大而
.
(2)函数y=-的图象在第
象限,在每一象限内,y随x的增大而
.
(3)函数y=,当x>0时,图象在第
象限,y随x的增大而
.
4.已知反比例函数y=.
(1)若函数的图象位于第一、三象限,则k
;
(2)若在每一象限内,y随x增大而增大,则k
.
5.函数y=kx-k与y=在同一直角坐标系中的图象可能是(
)
6.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是(
)
A.y=-5x-1
B.y=
C.y=-2x+2
D.y=4x
牢记函数图象的性质,严格按照函数图象性质判断.
课堂小结
反比例函数y=(k为常数,k≠0)的图象是双曲线;
当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小.
当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
1.y=(k≠0,k为常数)
2.列表
描点
连线
3.双曲线
4.第一、第三
第二、第四
【合作探究】
活动2
跟踪训练
1.第二个是y=-的图象.因为y=-中的k<0,图象在第二、四象限.
2.D
3.(1)一、三
减小
(2)二、四
增大
(3)一
减小
4.(1)<4
(2)>4
5.D
6.C
