26.1.2反比例函数的图象和性质的综合运用(第2课时)导学案
文档属性
| 名称 | 26.1.2反比例函数的图象和性质的综合运用(第2课时)导学案 | 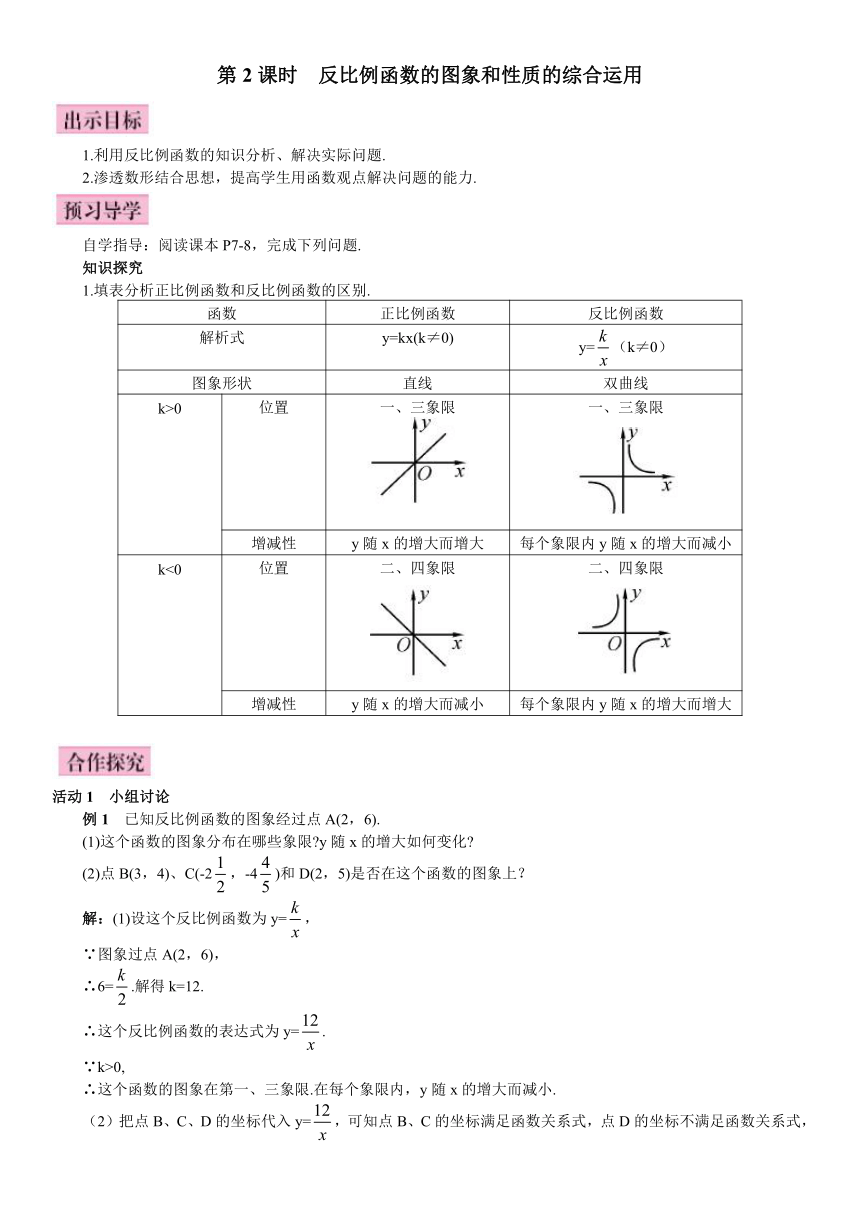 | |
| 格式 | zip | ||
| 文件大小 | 67.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 17:58:29 | ||
图片预览

文档简介
第2课时
反比例函数的图象和性质的综合运用
1.利用反比例函数的知识分析、解决实际问题.
2.渗透数形结合思想,提高学生用函数观点解决问题的能力.
自学指导:阅读课本P7-8,完成下列问题.
知识探究
1.填表分析正比例函数和反比例函数的区别.
函数
正比例函数
反比例函数
解析式
y=kx(k≠0)
y=(k≠0)
图象形状
直线
双曲线
k>0
位置
一、三象限
( http: / / www.21cnjy.com )
一、三象限
( http: / / www.21cnjy.com )
增减性
y随x的增大而增大
每个象限内y随x的增大而减小
k<0
位置
二、四象限
( http: / / www.21cnjy.com )
二、四象限
( http: / / www.21cnjy.com )
增减性
y随x的增大而减小
每个象限内y随x的增大而增大
活动1
小组讨论
例1
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限 y随x的增大如何变化
(2)点B(3,4)、C(-2,-4)和D(2,5)是否在这个函数的图象上?
解:(1)设这个反比例函数为y=,
∵图象过点A(2,6),
∴6=.解得k=12.
∴这个反比例函数的表达式为y=.
∵k>0,
∴这个函数的图象在第一、三象限.在每个象限内,y随x的增大而减小.
(2)把点B、C、D的坐标代入y=,可知点B、C的坐标满足函数关系式,点D的坐标不满足函数关系式,所以点B、C在函数y=的图象上,点D不在这个函数的图象上.
例2
如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
( http: / / www.21cnjy.com )
解:(1)反比例函数图象的分布只有两种可
( http: / / www.21cnjy.com )能,分布在第一、第三象限,或者分布在第二、第四象限.这个函数的图象的一支在第一象限,则另一支必在第三象限.
∵函数的图象在第一、第三象限,
∴m-5>0.解得m>5.
(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,
∴当a>a′>0和0>a>a′时b<b′;
当a>0>a′时b>b′.
活动2
跟踪训练
1.反比例函数y=的图象经过(2,-1),则k的值为
.
2.反比例函数y=的图象经过点(2,5),若点(1,n)在反比例函数图象上,则n等于(
)
A.10
B.
5
C.2
D.-6
3.下列各点在反比例函数y=-的图象上的是(
)
A.(-,-)
B.(-,)
C.(,)
D.(,)
4.在反比例函数y=的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),x1>x2>0>x3,则下列各式中正确的是(
)
A.y3>y1>y2
B.y3>y2>y1
C.y1>y2>y3
D.y1>y3>y2
因为k<0,所以图象在二、四象限;y随x的增大而增大.又x1>x2>0>x3,所以y1、y2在第四象限且0>y1>y2;y3在第二象限且y3>0,所以y3>y1>y2.
5.如图,点P是反比例函数y=图象上的一点,PD⊥x轴于D.则△POD的面积为
.
( http: / / www.21cnjy.com )
因为点P在图象上,所以n=,即mn=2;故S△ABC=OD·PD=mn=1.
6.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是
.
( http: / / www.21cnjy.com )
设函数为y=,而P在图象上,所以k=mn,又阴影部分面积是|mn|=3,函数图象在第二象限,所以k<0,即k=-3,所以函数关系是为y=-.
课堂小结
反比例函数图象和性质的综合运用.
教学至此,敬请使用学案当堂训练部分.
【合作探究】
活动2
跟踪训练
1.-2
2.A
3.B
4.A
5.1
6.y=-
反比例函数的图象和性质的综合运用
1.利用反比例函数的知识分析、解决实际问题.
2.渗透数形结合思想,提高学生用函数观点解决问题的能力.
自学指导:阅读课本P7-8,完成下列问题.
知识探究
1.填表分析正比例函数和反比例函数的区别.
函数
正比例函数
反比例函数
解析式
y=kx(k≠0)
y=(k≠0)
图象形状
直线
双曲线
k>0
位置
一、三象限
( http: / / www.21cnjy.com )
一、三象限
( http: / / www.21cnjy.com )
增减性
y随x的增大而增大
每个象限内y随x的增大而减小
k<0
位置
二、四象限
( http: / / www.21cnjy.com )
二、四象限
( http: / / www.21cnjy.com )
增减性
y随x的增大而减小
每个象限内y随x的增大而增大
活动1
小组讨论
例1
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限 y随x的增大如何变化
(2)点B(3,4)、C(-2,-4)和D(2,5)是否在这个函数的图象上?
解:(1)设这个反比例函数为y=,
∵图象过点A(2,6),
∴6=.解得k=12.
∴这个反比例函数的表达式为y=.
∵k>0,
∴这个函数的图象在第一、三象限.在每个象限内,y随x的增大而减小.
(2)把点B、C、D的坐标代入y=,可知点B、C的坐标满足函数关系式,点D的坐标不满足函数关系式,所以点B、C在函数y=的图象上,点D不在这个函数的图象上.
例2
如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
( http: / / www.21cnjy.com )
解:(1)反比例函数图象的分布只有两种可
( http: / / www.21cnjy.com )能,分布在第一、第三象限,或者分布在第二、第四象限.这个函数的图象的一支在第一象限,则另一支必在第三象限.
∵函数的图象在第一、第三象限,
∴m-5>0.解得m>5.
(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,
∴当a>a′>0和0>a>a′时b<b′;
当a>0>a′时b>b′.
活动2
跟踪训练
1.反比例函数y=的图象经过(2,-1),则k的值为
.
2.反比例函数y=的图象经过点(2,5),若点(1,n)在反比例函数图象上,则n等于(
)
A.10
B.
5
C.2
D.-6
3.下列各点在反比例函数y=-的图象上的是(
)
A.(-,-)
B.(-,)
C.(,)
D.(,)
4.在反比例函数y=的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),x1>x2>0>x3,则下列各式中正确的是(
)
A.y3>y1>y2
B.y3>y2>y1
C.y1>y2>y3
D.y1>y3>y2
因为k<0,所以图象在二、四象限;y随x的增大而增大.又x1>x2>0>x3,所以y1、y2在第四象限且0>y1>y2;y3在第二象限且y3>0,所以y3>y1>y2.
5.如图,点P是反比例函数y=图象上的一点,PD⊥x轴于D.则△POD的面积为
.
( http: / / www.21cnjy.com )
因为点P在图象上,所以n=,即mn=2;故S△ABC=OD·PD=mn=1.
6.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是
.
( http: / / www.21cnjy.com )
设函数为y=,而P在图象上,所以k=mn,又阴影部分面积是|mn|=3,函数图象在第二象限,所以k<0,即k=-3,所以函数关系是为y=-.
课堂小结
反比例函数图象和性质的综合运用.
教学至此,敬请使用学案当堂训练部分.
【合作探究】
活动2
跟踪训练
1.-2
2.A
3.B
4.A
5.1
6.y=-
