26.2实际问题与反比例函数导学案
图片预览

文档简介
26.2 实际问题与反比例函数
1.运用反比例函数解决实际问题.
2.把实际问题转化为反比例函数.
自学指导:阅读课本P12-15,完成下列问题.
知识探究
复习回顾:
(1)反比例函数y=(k为常数,k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每个象限内,y值随x值的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每个象限内,y值随x值的增大而增大;
(4)画函数图象的方法:列表→描点→连线.
自学反馈
1.地下室的体积V一定,那么底面积S和深度h的关系是 ;表达式是 .
2.运货物的路程s一定,那么运货物的速度v和时间t是 ;表达式是 .
3.电学知识告诉我们,用电器的输出功率P、两端的电压U和电器的电阻R有如下关系:PR=U2.这个关系式还可以写成P= ,或R= .
活动1 小组讨论
例1 市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积S定为500 m2,施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15 m时,碰上了坚硬的岩石.为了节约建设资金,公司临时改变计划,把储存室的深改为15 m,相应的,储存室的底面积应改为多少才能满足需要(保留两为小数)?
解:(1)根据圆柱体的体积公式,有
S·d=104.变形得S=
即储存室的底面积S是其深度d的反比例函数
(2)把S=500代入S=得:d=20
如果把储存室的底面积定为500 m2,施工时应向地下掘进20 m深.
(3)根据题意,把d=15代入S=得:S=≈666.67
当储存室的深为15 m时,储存室的底面积应改为666.67 m2才能满足需要.
例2 近视眼镜的度数y(度)与焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25 m.
(1)试求眼镜度数y与镜片焦距x之间的函数关系式;
(2)求1 000度近视眼镜镜片的焦距.
解:(1)设y=,
把x=0.25,y=400代入,得:400=,
所以,k=400×0.25=100
即所求的函数关系式为y=.
(2)当y=1 000时,1 000=,解得:x=0.1 m
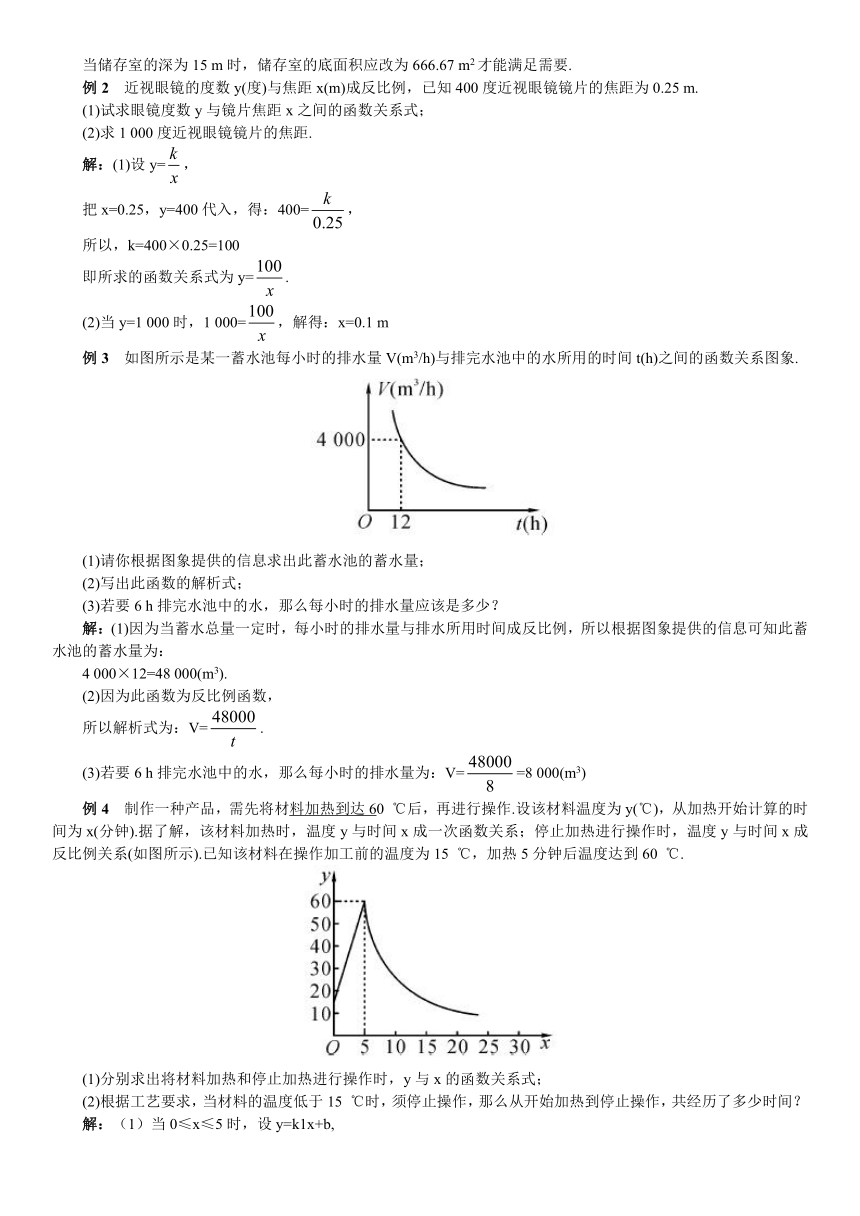
例3 如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
解:(1)因为当蓄水总量一定时,每小时的排水量与排水所用时间成反比例,所以根据图象提供的信息可知此蓄水池的蓄水量为:
4 000×12=48 000(m3).
(2)因为此函数为反比例函数,
所以解析式为:V=.
(3)若要6 h排完水池中的水,那么每小时的排水量为:V==8 000(m3)
例4 制作一种产品,需先将材料加热到达60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图所示).已知该材料在操作加工前的温度为15 ℃,加热5分钟后温度达到60 ℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
解:(1)当0≤x≤5时,设y=k1x+b,
由得
∴y=9x+15.
当x≥5时,设y=,
由x=5时,y=60知k2=300.
∴y=.
(2)当y=15时,由y=300x,得x=20.
故从开始加热到停止操作,共经历了20 min.
活动2 跟踪训练
1.A、B两城市相距720千米,一列火车从A城去B城.
(1)火车的速度v(千米/时)和行驶的时间t(时)之间的函数关系是 .
(2)若到达目的地后,按原路匀速返回,并要求在3小时内回到A城,则返回的速度不能低于 .
2.有一面积为60的梯形,其上底长是下底长的,若下底长为x,高为y,则y与x的函数关系是 .
3.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为( )
4.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100 m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系
B.菱形的面积为48 cm2,它的两条对角线的长为y(cm)与x(cm)的关系
C.一个玻璃容器的体积为30 L时,所盛液体的质量m与所盛液体的体积V之间的关系
D.压力为600 N时,压强p与受力面积S之间的关系
5.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )
6.为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知,药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此室内空气中每立方米的含药量为6毫克,请你根据题中所提供的信息,解答下列问题:
(1)药物燃烧时y关于x的函数关系式为:y=34x,自变量的取值范围是: ;药物燃烧后y与x的函数关系式为:y= ;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
课堂小结
利用反比例函数解决实际问题.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
1.反比例函数 S=
2.反比例函数 v=
3.
【合作探究】
活动2 跟踪训练
1.(1)v=
(2)240千米/小时
2.y=
3.A
4.C
5.C
6.(1)0≤x≤8
(2)30
(3)有效,因为燃烧时第4分钟含药量开始高于3毫克,当到第16分钟含药量开始低于3毫克,这样含药量不低于3毫克的时间共有16-4=12分钟,故有效.
1.运用反比例函数解决实际问题.
2.把实际问题转化为反比例函数.
自学指导:阅读课本P12-15,完成下列问题.
知识探究
复习回顾:
(1)反比例函数y=(k为常数,k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每个象限内,y值随x值的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每个象限内,y值随x值的增大而增大;
(4)画函数图象的方法:列表→描点→连线.
自学反馈
1.地下室的体积V一定,那么底面积S和深度h的关系是 ;表达式是 .
2.运货物的路程s一定,那么运货物的速度v和时间t是 ;表达式是 .
3.电学知识告诉我们,用电器的输出功率P、两端的电压U和电器的电阻R有如下关系:PR=U2.这个关系式还可以写成P= ,或R= .
活动1 小组讨论
例1 市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积S定为500 m2,施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15 m时,碰上了坚硬的岩石.为了节约建设资金,公司临时改变计划,把储存室的深改为15 m,相应的,储存室的底面积应改为多少才能满足需要(保留两为小数)?
解:(1)根据圆柱体的体积公式,有
S·d=104.变形得S=
即储存室的底面积S是其深度d的反比例函数
(2)把S=500代入S=得:d=20
如果把储存室的底面积定为500 m2,施工时应向地下掘进20 m深.
(3)根据题意,把d=15代入S=得:S=≈666.67
当储存室的深为15 m时,储存室的底面积应改为666.67 m2才能满足需要.
例2 近视眼镜的度数y(度)与焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25 m.
(1)试求眼镜度数y与镜片焦距x之间的函数关系式;
(2)求1 000度近视眼镜镜片的焦距.
解:(1)设y=,
把x=0.25,y=400代入,得:400=,
所以,k=400×0.25=100
即所求的函数关系式为y=.
(2)当y=1 000时,1 000=,解得:x=0.1 m
例3 如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
解:(1)因为当蓄水总量一定时,每小时的排水量与排水所用时间成反比例,所以根据图象提供的信息可知此蓄水池的蓄水量为:
4 000×12=48 000(m3).
(2)因为此函数为反比例函数,
所以解析式为:V=.
(3)若要6 h排完水池中的水,那么每小时的排水量为:V==8 000(m3)
例4 制作一种产品,需先将材料加热到达60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图所示).已知该材料在操作加工前的温度为15 ℃,加热5分钟后温度达到60 ℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
解:(1)当0≤x≤5时,设y=k1x+b,
由得
∴y=9x+15.
当x≥5时,设y=,
由x=5时,y=60知k2=300.
∴y=.
(2)当y=15时,由y=300x,得x=20.
故从开始加热到停止操作,共经历了20 min.
活动2 跟踪训练
1.A、B两城市相距720千米,一列火车从A城去B城.
(1)火车的速度v(千米/时)和行驶的时间t(时)之间的函数关系是 .
(2)若到达目的地后,按原路匀速返回,并要求在3小时内回到A城,则返回的速度不能低于 .
2.有一面积为60的梯形,其上底长是下底长的,若下底长为x,高为y,则y与x的函数关系是 .
3.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为( )
4.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100 m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系
B.菱形的面积为48 cm2,它的两条对角线的长为y(cm)与x(cm)的关系
C.一个玻璃容器的体积为30 L时,所盛液体的质量m与所盛液体的体积V之间的关系
D.压力为600 N时,压强p与受力面积S之间的关系
5.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )
6.为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知,药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此室内空气中每立方米的含药量为6毫克,请你根据题中所提供的信息,解答下列问题:
(1)药物燃烧时y关于x的函数关系式为:y=34x,自变量的取值范围是: ;药物燃烧后y与x的函数关系式为:y= ;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
课堂小结
利用反比例函数解决实际问题.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
1.反比例函数 S=
2.反比例函数 v=
3.
【合作探究】
活动2 跟踪训练
1.(1)v=
(2)240千米/小时
2.y=
3.A
4.C
5.C
6.(1)0≤x≤8
(2)30
(3)有效,因为燃烧时第4分钟含药量开始高于3毫克,当到第16分钟含药量开始低于3毫克,这样含药量不低于3毫克的时间共有16-4=12分钟,故有效.
