27.2.1平行线分线段成比例(第1课时)导学案
文档属性
| 名称 | 27.2.1平行线分线段成比例(第1课时)导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 100.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 00:00:00 | ||
图片预览

文档简介
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1.理解相似三角形的概念.
2.掌握平行线分线段成比例的基本事实及推论.
3.掌握判定三角形相似的预备定理.
阅读教材P29-31,自学“探究”与“思考”,弄懂相似三角形的概念,掌握平行线分线段成比例定理,理解相似三角形判定的预备定理.
自学反馈 学生独立完成后集体订正
①如果△ABC∽△A1B1C1的相似比为k,则△A1B1C1∽△ABC的相似比为 .
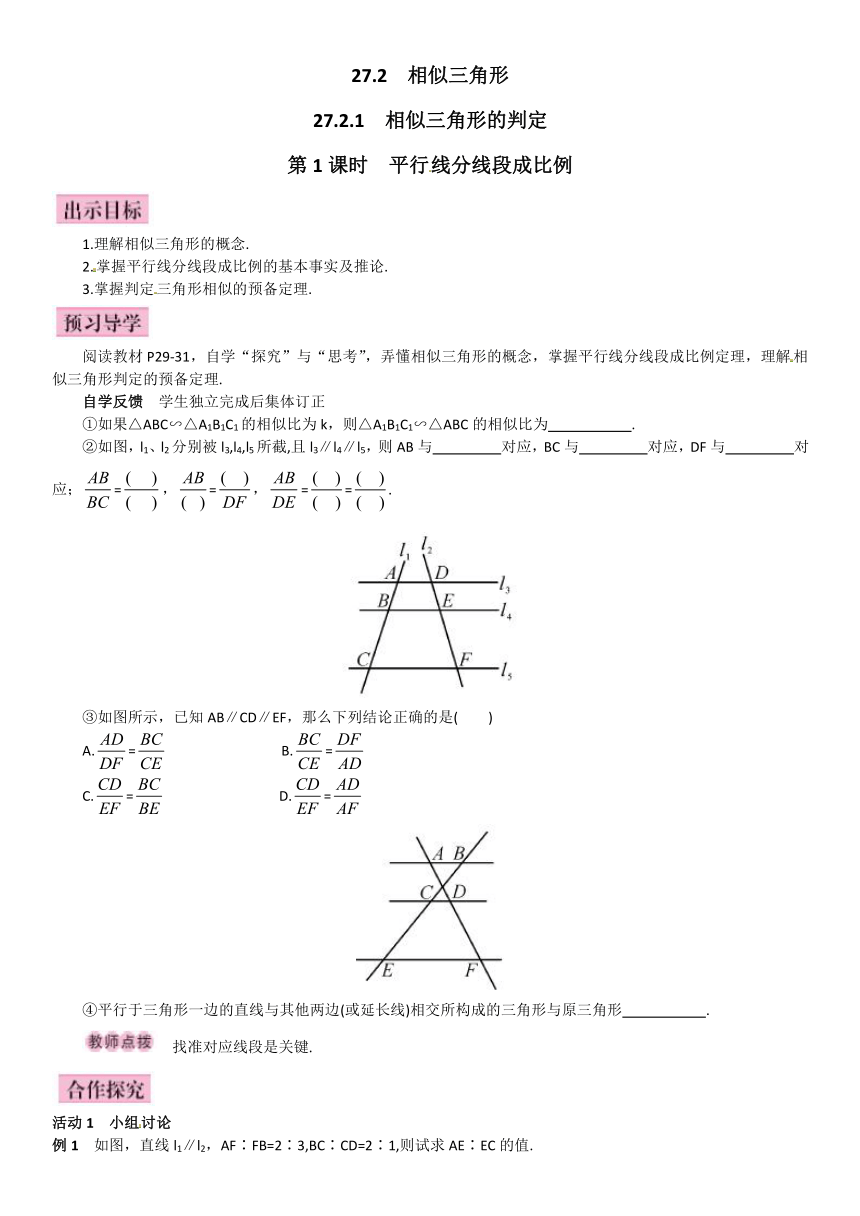
②如图,l1、l2分别被l3,l4,l5所截,且l3∥l4∥l5,则AB与 对应,BC与 对应,DF与 对应;=,=,==.
③如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
A.= B.=
C.= D.=
④平行于三角形一边的直线与其他两边(或延长线)相交所构成的三角形与原三角形 .
找准对应线段是关键.
活动1 小组讨论
例1 如图,直线l1∥l2,AF∶FB=2∶3,BC∶CD=2∶1,则试求AE∶EC的值.
解:∵l1∥l2,
∴△AGF∽△BDF,△AGE∽△CDE.
∴==,
∴AG=BD.
又∵=,BC+CD=BD,
∴CD=BD.
∴==2.即AE∶EC=2.
可从AE∶EC出发,只需要证得他们所在的两个三角形相似及他们的相似比即可,而AF与FB所在的两个三角形相似,两个相似关系可以得到线段AG、CD与线段BD的数量关系,从而就可以得出AG与CD的比,即△AGE与△CDE的相似比.
活动2 跟踪训练(独立完成后展示学习成果)
1.如图,ED∥BC,EC、BD相交于点A,过A的直线交ED、BC分别于点M、N,则图中有相似三角形( )
A.1对 B.2对 C.3对 D.4对
2.如图,DE∥BC,则下面比例式不成立的是( )
A.= B.= C.= D.=
3.如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
A.∠AEF=∠DEC B.FA∶CD=AE∶BC
C.FA∶AB=FE∶EC D.AB=DC
本题除运用相似三角形对应边的比相等外,还应根据图形对比例式进行适当的变形.
活动3 课堂小结
学生试述:这节课你学到了些什么?
教学至此,敬请使用学案当堂训练部分.
【预习导学1】
自学反馈
①
②DE EF AC = =
③A
④相似
【合作探究1】
活动2 跟踪训练
1.C
2.B
3.B
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1.理解相似三角形的概念.
2.掌握平行线分线段成比例的基本事实及推论.
3.掌握判定三角形相似的预备定理.
阅读教材P29-31,自学“探究”与“思考”,弄懂相似三角形的概念,掌握平行线分线段成比例定理,理解相似三角形判定的预备定理.
自学反馈 学生独立完成后集体订正
①如果△ABC∽△A1B1C1的相似比为k,则△A1B1C1∽△ABC的相似比为 .
②如图,l1、l2分别被l3,l4,l5所截,且l3∥l4∥l5,则AB与 对应,BC与 对应,DF与 对应;=,=,==.
③如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
A.= B.=
C.= D.=
④平行于三角形一边的直线与其他两边(或延长线)相交所构成的三角形与原三角形 .
找准对应线段是关键.
活动1 小组讨论
例1 如图,直线l1∥l2,AF∶FB=2∶3,BC∶CD=2∶1,则试求AE∶EC的值.
解:∵l1∥l2,
∴△AGF∽△BDF,△AGE∽△CDE.
∴==,
∴AG=BD.
又∵=,BC+CD=BD,
∴CD=BD.
∴==2.即AE∶EC=2.
可从AE∶EC出发,只需要证得他们所在的两个三角形相似及他们的相似比即可,而AF与FB所在的两个三角形相似,两个相似关系可以得到线段AG、CD与线段BD的数量关系,从而就可以得出AG与CD的比,即△AGE与△CDE的相似比.
活动2 跟踪训练(独立完成后展示学习成果)
1.如图,ED∥BC,EC、BD相交于点A,过A的直线交ED、BC分别于点M、N,则图中有相似三角形( )
A.1对 B.2对 C.3对 D.4对
2.如图,DE∥BC,则下面比例式不成立的是( )
A.= B.= C.= D.=
3.如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
A.∠AEF=∠DEC B.FA∶CD=AE∶BC
C.FA∶AB=FE∶EC D.AB=DC
本题除运用相似三角形对应边的比相等外,还应根据图形对比例式进行适当的变形.
活动3 课堂小结
学生试述:这节课你学到了些什么?
教学至此,敬请使用学案当堂训练部分.
【预习导学1】
自学反馈
①
②DE EF AC = =
③A
④相似
【合作探究1】
活动2 跟踪训练
1.C
2.B
3.B
