27.2.1相似三角形的判定定理1,2(第2课时)导学案
文档属性
| 名称 | 27.2.1相似三角形的判定定理1,2(第2课时)导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 63.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 00:00:00 | ||
图片预览

文档简介
第2课时 相似三角形的判定定理1,2
掌握三边成比例的两个三角形相似和两边成比例且夹角相等的两个三角形相似这两个判定三角形相似的定理.
[
阅读教材P32-34,自学“探究2”、“探究3”、“思考”与“例1”,掌握相似三角形判定定理1与判定定理2.
自学反馈 学生独立完成后集体订正
①如果两个三角形的三组边对应成比例,那么这两个三角形 .
②如果两个三角形的两组对应边的比相等,并且 相等,那么这两个三角形相似.
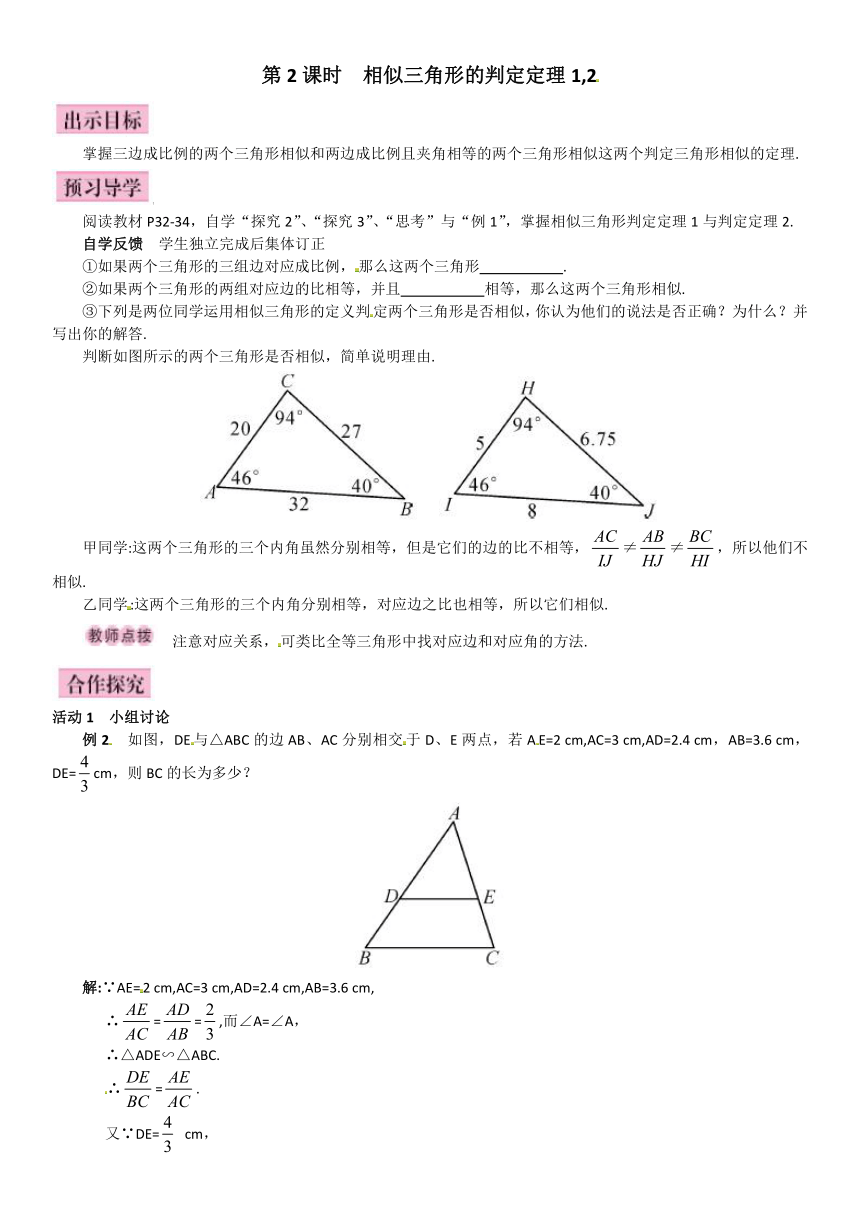
③下列是两位同学运用相似三角形的定义判定两个三角形是否相似,你认为他们的说法是否正确?为什么?并写出你的解答.
判断如图所示的两个三角形是否相似,简单说明理由.
甲同学:这两个三角形的三个内角虽然分别相等,但是它们的边的比不相等,≠≠,所以他们不相似.
乙同学:这两个三角形的三个内角分别相等,对应边之比也相等,所以它们相似.
注意对应关系,可类比全等三角形中找对应边和对应角的方法.
活动1 小组讨论
例2 如图,DE与△ABC的边AB、AC分别相交于D、E两点,若AE=2 cm,AC=3 cm,AD=2.4 cm,AB=3.6 cm,DE=cm,则BC的长为多少?
解:∵AE=2 cm,AC=3 cm,AD=2.4 cm,AB=3.6 cm,
∴==,而∠A=∠A,
∴△ADE∽△ABC.
∴=.
又∵DE= cm,
∴=,
∴BC=2 cm.
运用相似三角形可以进行边的计算.
活动2 跟踪训练(独立完成后展示学习成果)
1.如图,在□ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF和△CDE相似,则BF长为多少?
在要使判断的两个三角形相似时,有一个角相等的情况下,夹这角的两边的比相等时有两种情形,不要只考虑一种情形,而忽视了另一种情形.
2.如图所示,DE∥FG∥BC,图中共有相似三角形( )
A.1对 B.2对 C.3对 D.4对
按照一定的顺序去寻找相似三角形.
活动3 课堂小结
学生试述:这节课你学到了些什么?
教学至此,敬请使用学案当堂训练部分.
【预习导学2】
自学反馈
①相似
②所夹的角
③略
【合作探究2】
活动2 跟踪训练
1.1.8
2.C
掌握三边成比例的两个三角形相似和两边成比例且夹角相等的两个三角形相似这两个判定三角形相似的定理.
[
阅读教材P32-34,自学“探究2”、“探究3”、“思考”与“例1”,掌握相似三角形判定定理1与判定定理2.
自学反馈 学生独立完成后集体订正
①如果两个三角形的三组边对应成比例,那么这两个三角形 .
②如果两个三角形的两组对应边的比相等,并且 相等,那么这两个三角形相似.
③下列是两位同学运用相似三角形的定义判定两个三角形是否相似,你认为他们的说法是否正确?为什么?并写出你的解答.
判断如图所示的两个三角形是否相似,简单说明理由.
甲同学:这两个三角形的三个内角虽然分别相等,但是它们的边的比不相等,≠≠,所以他们不相似.
乙同学:这两个三角形的三个内角分别相等,对应边之比也相等,所以它们相似.
注意对应关系,可类比全等三角形中找对应边和对应角的方法.
活动1 小组讨论
例2 如图,DE与△ABC的边AB、AC分别相交于D、E两点,若AE=2 cm,AC=3 cm,AD=2.4 cm,AB=3.6 cm,DE=cm,则BC的长为多少?
解:∵AE=2 cm,AC=3 cm,AD=2.4 cm,AB=3.6 cm,
∴==,而∠A=∠A,
∴△ADE∽△ABC.
∴=.
又∵DE= cm,
∴=,
∴BC=2 cm.
运用相似三角形可以进行边的计算.
活动2 跟踪训练(独立完成后展示学习成果)
1.如图,在□ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF和△CDE相似,则BF长为多少?
在要使判断的两个三角形相似时,有一个角相等的情况下,夹这角的两边的比相等时有两种情形,不要只考虑一种情形,而忽视了另一种情形.
2.如图所示,DE∥FG∥BC,图中共有相似三角形( )
A.1对 B.2对 C.3对 D.4对
按照一定的顺序去寻找相似三角形.
活动3 课堂小结
学生试述:这节课你学到了些什么?
教学至此,敬请使用学案当堂训练部分.
【预习导学2】
自学反馈
①相似
②所夹的角
③略
【合作探究2】
活动2 跟踪训练
1.1.8
2.C
