27.2.1相似三角形的判定定理3(第3课时)导学案
文档属性
| 名称 | 27.2.1相似三角形的判定定理3(第3课时)导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 107.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 00:00:00 | ||
图片预览

文档简介
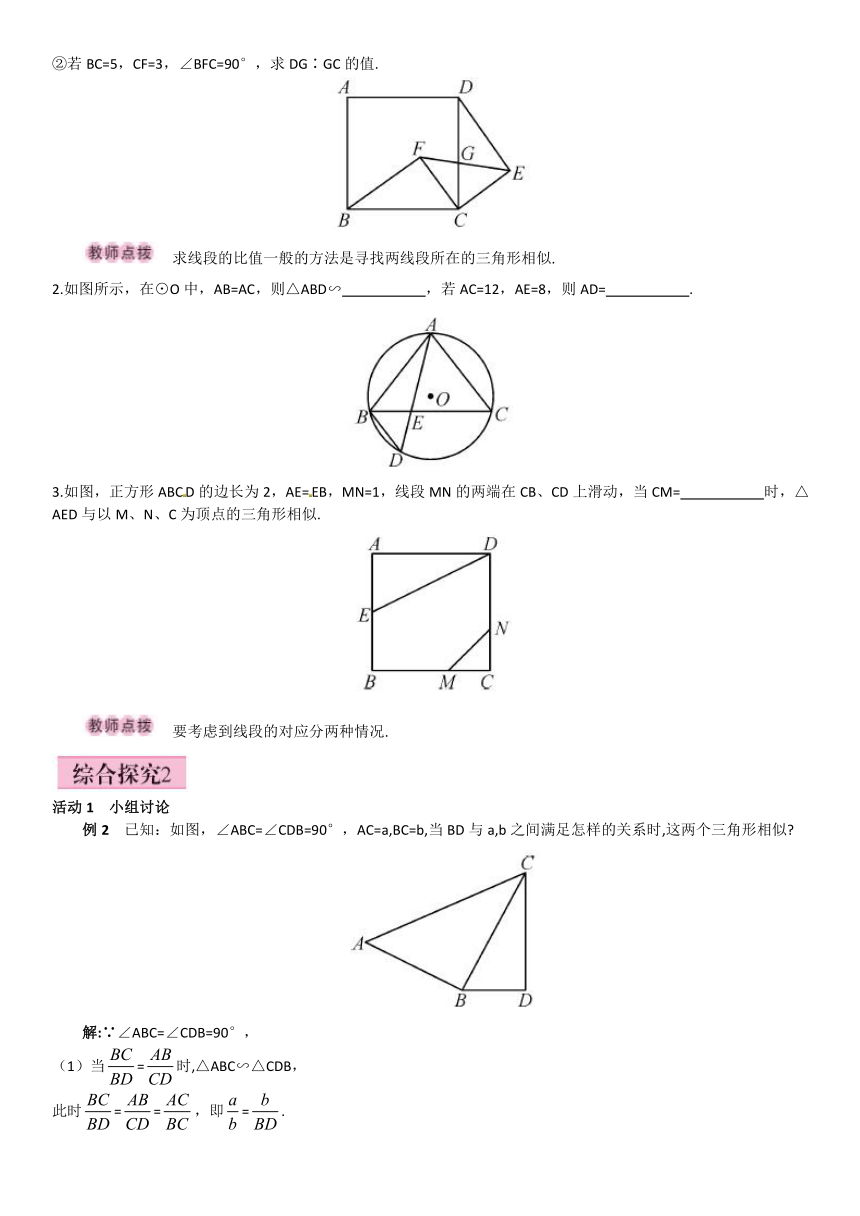
第3课时 相似三角形的判定定理3
1.掌握相似三角形的判定定理3.
2.了解两个直角三角形相似的判定方法.
3.深化对相似三角形的三个判定方法的理解,并能够运用相似三角形的判定方法解决相似三角形的有关问题.
阅读教材P35-36,自学“例2”与“思考”,理解相似三角形判定定理3及直角三角形相似的判定方法.
自学反馈 学生独立完成后集体订正
①如果一个三角形的两个角与另一个三角形的两个角对应 ,那么这两个三角形相似.
②如果两个直角三角形中,有一条直角边和斜边对应成比例,那么这两个直角三角形 .
③要判定两个直角三角形相似,最简单的方法就是再找 对应相等,就可以根据相似三角形的判定3,判定这两个直角三角形相似.
④如图所示,已知∠ADE=∠B,则△AED∽ .理由是 .
⑤顶角对应相等的两个等腰三角形相似吗?为什么?
要根据已知条件选择适当的方法.
活动1 小组讨论
例1 如图,在△ABC中,∠C=60°,BE⊥AC于E,AD⊥BC于D.
求证:△CDE∽△CAB.
证明:∵∠C+∠CAD=90°,∠C+∠CBE=90°,
∴∠CAD=∠CBE.
又∵∠C=∠C,∴△CAD∽△CBE.
∴=.
又∵∠C=∠C,∴△CDE∽△CAB
在寻求不到另一个角相等的情况下,寻求夹相等的角的两边的比相等,是解本类题型的有效方法.
活动2 跟踪训练(独立完成后展示学习成果)
1.如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
①求证:△BCF∽△DCE;
②若BC=5,CF=3,∠BFC=90°,求DG∶GC的值.
求线段的比值一般的方法是寻找两线段所在的三角形相似.
2.如图所示,在⊙O中,AB=AC,则△ABD∽ ,若AC=12,AE=8,则AD= .
3.如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM= 时,△AED与以M、N、C为顶点的三角形相似.
要考虑到线段的对应分两种情况.
活动1 小组讨论
例2 已知:如图,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系时,这两个三角形相似?
解:∵∠ABC=∠CDB=90°,
(1)当=时,△ABC∽△CDB,
此时==,即=.
∴BD=.
即当BD=时,△ABC∽△CDB;
(2)当=时,△ABC∽△BDC,
此时==,即=.
∴=,BD=.
∴当BD=时,△ABC∽△BDC.
综上所述,即当BD=或BD=时,这两个三角形相似.
本题仍是要考虑当两个三角形有一个角相等时,夹这个角的两边的比相等时有两种情况.
活动2 跟踪训练(独立完成后展示学习成果)
如图,在△ABC中,∠C=90°,BC=8 cm,4AC-3BC=0,点P从B点出发,沿BC方向以2 cm/s的速度移动,点Q从C点出发,沿CA方向以1 cm/s的速度移动,若P、Q分别从B、C同时出发,经过多少秒时,△CPQ与△CBA相似?
活动3 课堂小结
1.本节学习的数学知识:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
2.根据题目的具体情况,选择适当的方法证明三角形相似.
3.本节学习的数学思想:数形结合、分类讨论.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
①相等
②相似
③一个锐角
④△ACB 略
⑤相似 略
【合作探究1】
活动2 跟踪训练
1.①略 ②4∶3
2.△AEB 18
3.或
【合作探究2】
活动2 跟踪训练
设经过t s时,△CPQ和△CBA相似,此时BP=2t cm,CQ=t cm,则CP=(8-2t) cm,其中0又BC=8 cm,4AC-3BC=0,求得AC=6 cm.
(1)当PQ∥AB时,△CPQ∽△CBA,则=,即=,所以t=2.4.
(2)当=时,△CPQ∽△CAB,则=,解得t=.
故经过2.4 s或 s时,△CPQ与△CBA相似.
1.掌握相似三角形的判定定理3.
2.了解两个直角三角形相似的判定方法.
3.深化对相似三角形的三个判定方法的理解,并能够运用相似三角形的判定方法解决相似三角形的有关问题.
阅读教材P35-36,自学“例2”与“思考”,理解相似三角形判定定理3及直角三角形相似的判定方法.
自学反馈 学生独立完成后集体订正
①如果一个三角形的两个角与另一个三角形的两个角对应 ,那么这两个三角形相似.
②如果两个直角三角形中,有一条直角边和斜边对应成比例,那么这两个直角三角形 .
③要判定两个直角三角形相似,最简单的方法就是再找 对应相等,就可以根据相似三角形的判定3,判定这两个直角三角形相似.
④如图所示,已知∠ADE=∠B,则△AED∽ .理由是 .
⑤顶角对应相等的两个等腰三角形相似吗?为什么?
要根据已知条件选择适当的方法.
活动1 小组讨论
例1 如图,在△ABC中,∠C=60°,BE⊥AC于E,AD⊥BC于D.
求证:△CDE∽△CAB.
证明:∵∠C+∠CAD=90°,∠C+∠CBE=90°,
∴∠CAD=∠CBE.
又∵∠C=∠C,∴△CAD∽△CBE.
∴=.
又∵∠C=∠C,∴△CDE∽△CAB
在寻求不到另一个角相等的情况下,寻求夹相等的角的两边的比相等,是解本类题型的有效方法.
活动2 跟踪训练(独立完成后展示学习成果)
1.如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
①求证:△BCF∽△DCE;
②若BC=5,CF=3,∠BFC=90°,求DG∶GC的值.
求线段的比值一般的方法是寻找两线段所在的三角形相似.
2.如图所示,在⊙O中,AB=AC,则△ABD∽ ,若AC=12,AE=8,则AD= .
3.如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM= 时,△AED与以M、N、C为顶点的三角形相似.
要考虑到线段的对应分两种情况.
活动1 小组讨论
例2 已知:如图,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系时,这两个三角形相似?
解:∵∠ABC=∠CDB=90°,
(1)当=时,△ABC∽△CDB,
此时==,即=.
∴BD=.
即当BD=时,△ABC∽△CDB;
(2)当=时,△ABC∽△BDC,
此时==,即=.
∴=,BD=.
∴当BD=时,△ABC∽△BDC.
综上所述,即当BD=或BD=时,这两个三角形相似.
本题仍是要考虑当两个三角形有一个角相等时,夹这个角的两边的比相等时有两种情况.
活动2 跟踪训练(独立完成后展示学习成果)
如图,在△ABC中,∠C=90°,BC=8 cm,4AC-3BC=0,点P从B点出发,沿BC方向以2 cm/s的速度移动,点Q从C点出发,沿CA方向以1 cm/s的速度移动,若P、Q分别从B、C同时出发,经过多少秒时,△CPQ与△CBA相似?
活动3 课堂小结
1.本节学习的数学知识:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
2.根据题目的具体情况,选择适当的方法证明三角形相似.
3.本节学习的数学思想:数形结合、分类讨论.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
①相等
②相似
③一个锐角
④△ACB 略
⑤相似 略
【合作探究1】
活动2 跟踪训练
1.①略 ②4∶3
2.△AEB 18
3.或
【合作探究2】
活动2 跟踪训练
设经过t s时,△CPQ和△CBA相似,此时BP=2t cm,CQ=t cm,则CP=(8-2t) cm,其中0
(1)当PQ∥AB时,△CPQ∽△CBA,则=,即=,所以t=2.4.
(2)当=时,△CPQ∽△CAB,则=,解得t=.
故经过2.4 s或 s时,△CPQ与△CBA相似.
