27.3.1位似图形的概念及画法导学案
图片预览
文档简介
27.3 位似
第1课时 位似图形的概念及画法
1.正确理解位似图形等有关概念,能够按照要求利用位似将图形进行放大或缩小以及能够正确地作出位似图形的位似中心.
2.在实际操作和探究活动中,让学生感受、体会到几何图形之美,提高对数学美的认识层次,陶冶美育情操,激发学习热情.
阅读教材P47-48,自学“思考”与“探究”,理解位似的概念,会找出位似图形的位似中心,并能按要求将图形进行放大或缩小的位似变换.
自学反馈 学生独立完成后集体订正
①两个多边形不仅 ,而且对应点的连线相交于一点,对应边互相 ,像这样的两个图形叫做位似图形,这个点叫做 .
②下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等
B.两个图形如果是位似图形,那么这两个图形不一定相似
C.两个图形如果是相似图形,那么这两个图形一定位似
D.两个图形如果是位似图形,那么这两个图形一定相似
③用作位似图形的方法,可以将一个图形放大或缩小,位似中心位置可能在( )
A.原图形的外部 B.原图形的内部
C.原图形的边上 D.任意位置
位似的三要素即是判定位似的依据,也是位似图形的性质.
活动1 小组讨论
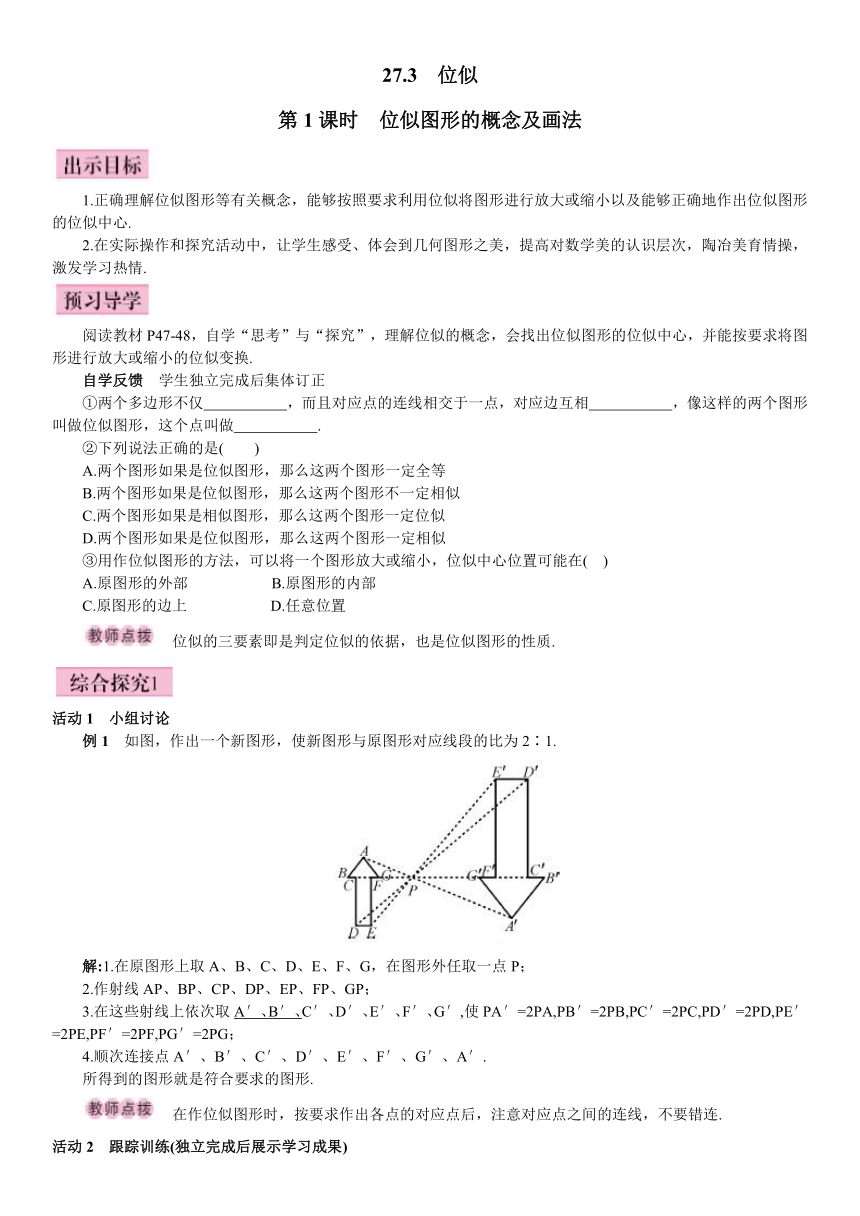
例1 如图,作出一个新图形,使新图形与原图形对应线段的比为2∶1.
解:1.在原图形上取A、B、C、D、E、F、G,在图形外任取一点P;
2.作射线AP、BP、CP、DP、EP、FP、GP;
3.在这些射线上依次取A′、B′、C′、D′、E′、F′、G′,使PA′=2PA,PB′=2PB,PC′=2PC,PD′=2PD,PE′=2PE,PF′=2PF,PG′=2PG;
4.顺次连接点A′、B′、C′、D′、E′、F′、G′、A′.
所得到的图形就是符合要求的图形.
在作位似图形时,按要求作出各点的对应点后,注意对应点之间的连线,不要错连.
活动2 跟踪训练(独立完成后展示学习成果)
1.例1中的位似中心为点 ,如果把位似中心选在原图形的内部,那么所得图形是怎样的?如果点A′、B′、C′、D′、E′、F′、G′取在AP、BP、CP、DP、EP、FP、GP的延长线上时,所得的图形又是怎样的?(试着画一画)
当位似中心在原图形的外部时,两个图形可能在位似中心的两侧或同侧.
2.如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?
3.如图,以O为位似中心,将△ABC放大为原来的两倍.
第2小题可根据位似的三要素得出对应线段平行;第3小题可有两种情况,画出其中一种即可.
4.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′= .
活动1 小组讨论
例2 请画出如图所示两个图形的位似中心.
解:如图所示的点O1,就是图1的位似中心.
如图所示的点O2,就是图2的位似中心.
正确地作出位似中心,是解位似图形的关键,可以根据位似中心的定义,位似图形的对应点连线的交点就是位似中心.
活动2 跟踪训练(独立完成后展示学习成果)
如图,图中的小方格都是边长为1的正方形,△ABC与△A1B1C1是以点O为位似中心的位似图形,它们的顶点都是在小正方形的顶点上.
①画出位似中心点O;
②求出△ABC与△A1B1C1的相似比;
③以点O为位似中心,再画一个△A2B2C2,使它与△ABC的相似比等于1.5
活动3 课堂小结
学生试述:这节课你学到了些什么?
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
①相似 平行 位似中心
②D
③D
【合作探究1】
活动2 跟踪训练
1.P 略
2.平行 因为位似的两个图形的对应边平行
3.略
4.2
【合作探究2】
活动2 跟踪训练
①略
②
③略
第1课时 位似图形的概念及画法
1.正确理解位似图形等有关概念,能够按照要求利用位似将图形进行放大或缩小以及能够正确地作出位似图形的位似中心.
2.在实际操作和探究活动中,让学生感受、体会到几何图形之美,提高对数学美的认识层次,陶冶美育情操,激发学习热情.
阅读教材P47-48,自学“思考”与“探究”,理解位似的概念,会找出位似图形的位似中心,并能按要求将图形进行放大或缩小的位似变换.
自学反馈 学生独立完成后集体订正
①两个多边形不仅 ,而且对应点的连线相交于一点,对应边互相 ,像这样的两个图形叫做位似图形,这个点叫做 .
②下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等
B.两个图形如果是位似图形,那么这两个图形不一定相似
C.两个图形如果是相似图形,那么这两个图形一定位似
D.两个图形如果是位似图形,那么这两个图形一定相似
③用作位似图形的方法,可以将一个图形放大或缩小,位似中心位置可能在( )
A.原图形的外部 B.原图形的内部
C.原图形的边上 D.任意位置
位似的三要素即是判定位似的依据,也是位似图形的性质.
活动1 小组讨论
例1 如图,作出一个新图形,使新图形与原图形对应线段的比为2∶1.
解:1.在原图形上取A、B、C、D、E、F、G,在图形外任取一点P;
2.作射线AP、BP、CP、DP、EP、FP、GP;
3.在这些射线上依次取A′、B′、C′、D′、E′、F′、G′,使PA′=2PA,PB′=2PB,PC′=2PC,PD′=2PD,PE′=2PE,PF′=2PF,PG′=2PG;
4.顺次连接点A′、B′、C′、D′、E′、F′、G′、A′.
所得到的图形就是符合要求的图形.
在作位似图形时,按要求作出各点的对应点后,注意对应点之间的连线,不要错连.
活动2 跟踪训练(独立完成后展示学习成果)
1.例1中的位似中心为点 ,如果把位似中心选在原图形的内部,那么所得图形是怎样的?如果点A′、B′、C′、D′、E′、F′、G′取在AP、BP、CP、DP、EP、FP、GP的延长线上时,所得的图形又是怎样的?(试着画一画)
当位似中心在原图形的外部时,两个图形可能在位似中心的两侧或同侧.
2.如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?
3.如图,以O为位似中心,将△ABC放大为原来的两倍.
第2小题可根据位似的三要素得出对应线段平行;第3小题可有两种情况,画出其中一种即可.
4.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′= .
活动1 小组讨论
例2 请画出如图所示两个图形的位似中心.
解:如图所示的点O1,就是图1的位似中心.
如图所示的点O2,就是图2的位似中心.
正确地作出位似中心,是解位似图形的关键,可以根据位似中心的定义,位似图形的对应点连线的交点就是位似中心.
活动2 跟踪训练(独立完成后展示学习成果)
如图,图中的小方格都是边长为1的正方形,△ABC与△A1B1C1是以点O为位似中心的位似图形,它们的顶点都是在小正方形的顶点上.
①画出位似中心点O;
②求出△ABC与△A1B1C1的相似比;
③以点O为位似中心,再画一个△A2B2C2,使它与△ABC的相似比等于1.5
活动3 课堂小结
学生试述:这节课你学到了些什么?
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
①相似 平行 位似中心
②D
③D
【合作探究1】
活动2 跟踪训练
1.P 略
2.平行 因为位似的两个图形的对应边平行
3.略
4.2
【合作探究2】
活动2 跟踪训练
①略
②
③略
