27.3.2平面直角坐标系中的位似导学案
文档属性
| 名称 | 27.3.2平面直角坐标系中的位似导学案 | 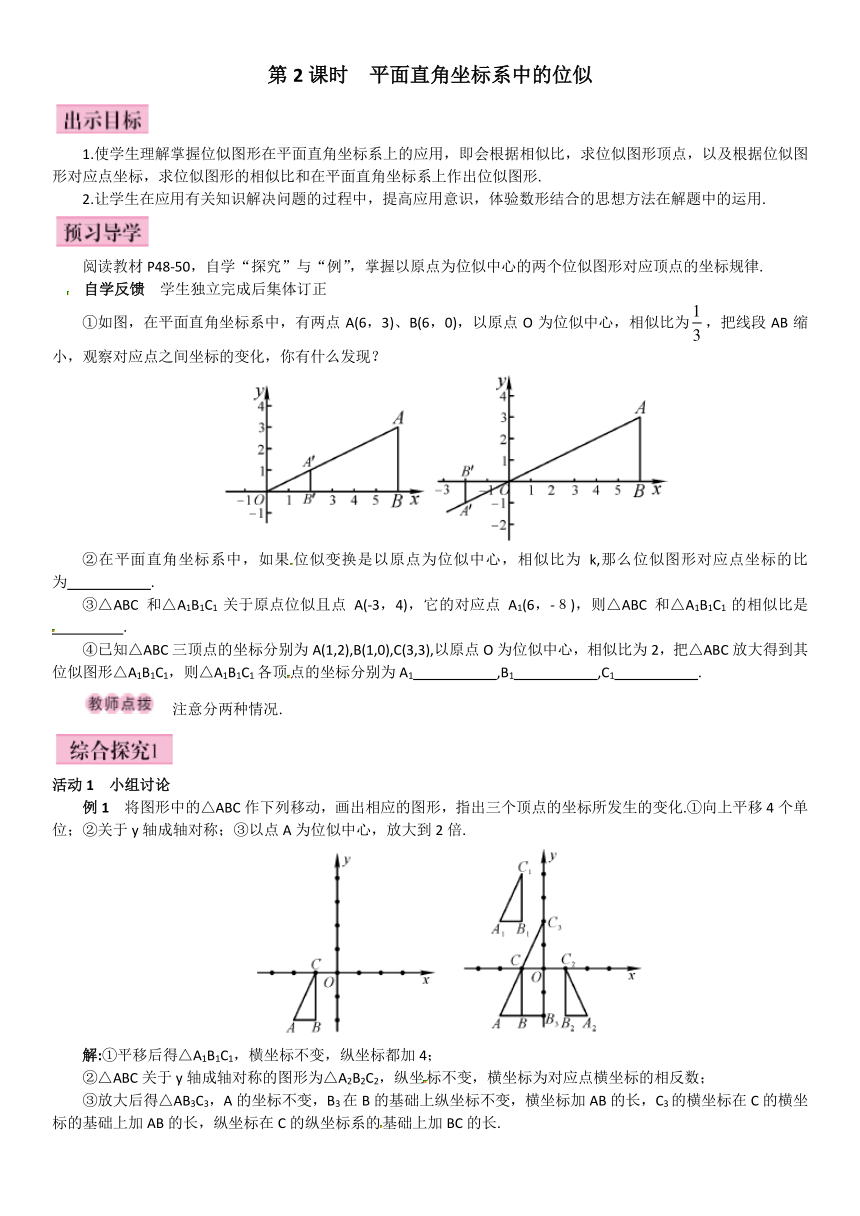 | |
| 格式 | zip | ||
| 文件大小 | 73.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 18:39:27 | ||
图片预览

文档简介
第2课时 平面直角坐标系中的位似
1.使学生理解掌握位似图形在平面直角坐标系上的应用,即会根据相似比,求位似图形顶点,以及根据位似图形对应点坐标,求位似图形的相似比和在平面直角坐标系上作出位似图形.
2.让学生在应用有关知识解决问题的过程中,提高应用意识,体验数形结合的思想方法在解题中的运用.
阅读教材P48-50,自学“探究”与“例”,掌握以原点为位似中心的两个位似图形对应顶点的坐标规律.
自学反馈 学生独立完成后集体订正
①如图,在平面直角坐标系中,有两点A(6,3)、B(6,0),以原点O为位似中心,相似比为,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
②在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点坐标的比为 .
③△ABC和△A1B1C1关于原点位似且点A(-3,4),它的对应点A1(6,-8),则△ABC和△A1B1C1的相似比是 .
④已知△ABC三顶点的坐标分别为A(1,2),B(1,0),C(3,3),以原点O为位似中心,相似比为2,把△ABC放大得到其位似图形△A1B1C1,则△A1B1C1各顶点的坐标分别为A1 ,B1 ,C1 .
注意分两种情况.
活动1 小组讨论
例1 将图形中的△ABC作下列移动,画出相应的图形,指出三个顶点的坐标所发生的变化.①向上平移4个单位;②关于y轴成轴对称;③以点A为位似中心,放大到2倍.
解:①平移后得△A1B1C1,横坐标不变,纵坐标都加4;
②△ABC关于y轴成轴对称的图形为△A2B2C2,纵坐标不变,横坐标为对应点横坐标的相反数;
③放大后得△AB3C3,A的坐标不变,B3在B的基础上纵坐标不变,横坐标加AB的长,C3的横坐标在C的横坐标的基础上加AB的长,纵坐标在C的纵坐标系的基础上加BC的长.
考虑图形在平面直角坐标系中作何种变换,弄清点的坐标的变化情况;作位似变换时,求出顶点坐标即可.
活动2 跟踪训练(独立完成后展示学习成果)
1.某个图形上各点的横、纵坐标都变成原来的,连接各点所得图形与原图形相比( )
A.完全没有变化 B.扩大成原来的2倍
C.面积缩小为原来的 D.关于纵轴成轴对称
2.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个 B.可以有2个
C.有2个以上但有限 D.有无数个
活动1 小组讨论
例2 如图所示的△ABC,以A点为位似中心,放大为原来的2倍,画出一个相应的图形,并写出相应的点的坐标.
解:根据题意,图中的△AB1C1就是满足题意的三角形,其中A点的坐标不变,仍是(-3,-1),B1、C1的坐标分别为(3,-3),(1,3).
解决本题的关键就是要作出正确的图形,否则求出的点的坐标就会发生错误.
活动2 跟踪训练(独立完成后展示学习成果)
在平面直角坐标系中,将坐标为(0,0)、(2,4)、(2,0)、(4,4)、(6,0)的点用线段顺次连结起来形成一个图案.
①将这五个点的纵坐标不变,横坐标变为原来的,求上述点的坐标,将所得的五个点用线段顺次连接起来,所得图案与原图案相比有什么变化?
②横坐标不变,纵坐标分别减去3呢?
③横坐标都加上3,纵坐标不变呢?
④横、纵坐标都乘以-1呢?
⑤横、纵坐标分别变成原来的2倍呢?面积如何变化?
活动3 课堂小结
1.本节学习的数学知识:以原点为位似中心,位似图形对应点之间的坐标的关系.
2.本节学习的数学方法:运用数形结合的方法解题.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
①略
②k或-k
③
④A1(2,4)或(-2,-4)、B2(2,0)或(-2,0)、C1(6,6)或(-6,-6)
【合作探究1】
活动2 跟踪训练
1.C
2.B
【合作探究2】
活动2 跟踪训练
①横向缩小
②向下平移3个单位长度
③向右平移3个单位长度
④关于原点作中心对称变换
⑤以原点为位似中心作位似变换,相似比为2,面积扩大4倍
1.使学生理解掌握位似图形在平面直角坐标系上的应用,即会根据相似比,求位似图形顶点,以及根据位似图形对应点坐标,求位似图形的相似比和在平面直角坐标系上作出位似图形.
2.让学生在应用有关知识解决问题的过程中,提高应用意识,体验数形结合的思想方法在解题中的运用.
阅读教材P48-50,自学“探究”与“例”,掌握以原点为位似中心的两个位似图形对应顶点的坐标规律.
自学反馈 学生独立完成后集体订正
①如图,在平面直角坐标系中,有两点A(6,3)、B(6,0),以原点O为位似中心,相似比为,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
②在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点坐标的比为 .
③△ABC和△A1B1C1关于原点位似且点A(-3,4),它的对应点A1(6,-8),则△ABC和△A1B1C1的相似比是 .
④已知△ABC三顶点的坐标分别为A(1,2),B(1,0),C(3,3),以原点O为位似中心,相似比为2,把△ABC放大得到其位似图形△A1B1C1,则△A1B1C1各顶点的坐标分别为A1 ,B1 ,C1 .
注意分两种情况.
活动1 小组讨论
例1 将图形中的△ABC作下列移动,画出相应的图形,指出三个顶点的坐标所发生的变化.①向上平移4个单位;②关于y轴成轴对称;③以点A为位似中心,放大到2倍.
解:①平移后得△A1B1C1,横坐标不变,纵坐标都加4;
②△ABC关于y轴成轴对称的图形为△A2B2C2,纵坐标不变,横坐标为对应点横坐标的相反数;
③放大后得△AB3C3,A的坐标不变,B3在B的基础上纵坐标不变,横坐标加AB的长,C3的横坐标在C的横坐标的基础上加AB的长,纵坐标在C的纵坐标系的基础上加BC的长.
考虑图形在平面直角坐标系中作何种变换,弄清点的坐标的变化情况;作位似变换时,求出顶点坐标即可.
活动2 跟踪训练(独立完成后展示学习成果)
1.某个图形上各点的横、纵坐标都变成原来的,连接各点所得图形与原图形相比( )
A.完全没有变化 B.扩大成原来的2倍
C.面积缩小为原来的 D.关于纵轴成轴对称
2.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个 B.可以有2个
C.有2个以上但有限 D.有无数个
活动1 小组讨论
例2 如图所示的△ABC,以A点为位似中心,放大为原来的2倍,画出一个相应的图形,并写出相应的点的坐标.
解:根据题意,图中的△AB1C1就是满足题意的三角形,其中A点的坐标不变,仍是(-3,-1),B1、C1的坐标分别为(3,-3),(1,3).
解决本题的关键就是要作出正确的图形,否则求出的点的坐标就会发生错误.
活动2 跟踪训练(独立完成后展示学习成果)
在平面直角坐标系中,将坐标为(0,0)、(2,4)、(2,0)、(4,4)、(6,0)的点用线段顺次连结起来形成一个图案.
①将这五个点的纵坐标不变,横坐标变为原来的,求上述点的坐标,将所得的五个点用线段顺次连接起来,所得图案与原图案相比有什么变化?
②横坐标不变,纵坐标分别减去3呢?
③横坐标都加上3,纵坐标不变呢?
④横、纵坐标都乘以-1呢?
⑤横、纵坐标分别变成原来的2倍呢?面积如何变化?
活动3 课堂小结
1.本节学习的数学知识:以原点为位似中心,位似图形对应点之间的坐标的关系.
2.本节学习的数学方法:运用数形结合的方法解题.
教学至此,敬请使用学案当堂训练部分.
【预习导学】
自学反馈
①略
②k或-k
③
④A1(2,4)或(-2,-4)、B2(2,0)或(-2,0)、C1(6,6)或(-6,-6)
【合作探究1】
活动2 跟踪训练
1.C
2.B
【合作探究2】
活动2 跟踪训练
①横向缩小
②向下平移3个单位长度
③向右平移3个单位长度
④关于原点作中心对称变换
⑤以原点为位似中心作位似变换,相似比为2,面积扩大4倍
