人教版数学八年级上册12.2三角形全等的判定第1课时
文档属性
| 名称 | 人教版数学八年级上册12.2三角形全等的判定第1课时 |

|
|
| 格式 | zip | ||
| 文件大小 | 444.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-12 00:00:00 | ||
图片预览




文档简介
课件28张PPT。12.2.1 三角形全等的判定
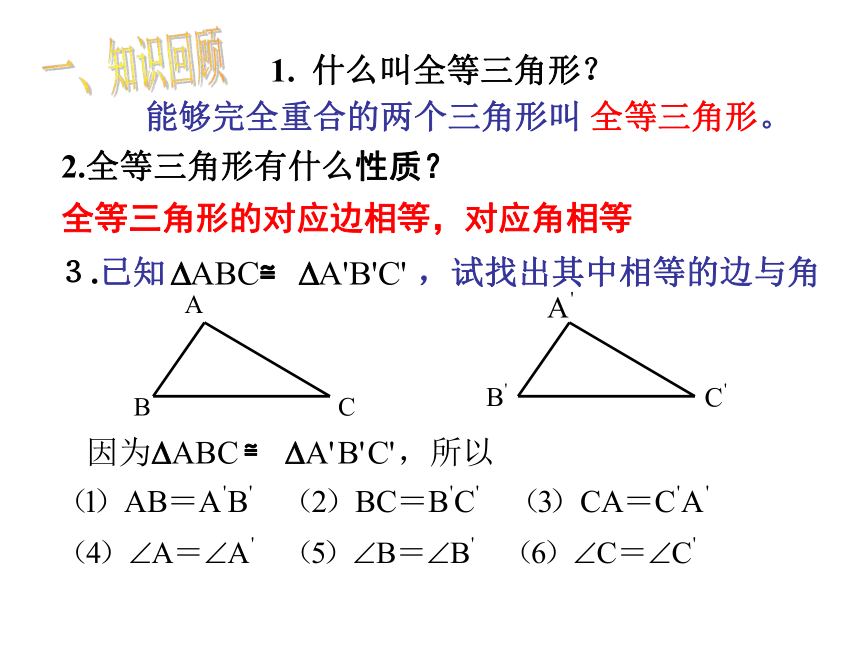
(第1课时)一、知识回顾 1. 什么叫全等三角形?能够完全重合的两个三角形叫 全等三角形。2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等≌两块完全一样的三角形,就是两个三角形全等.
什么样的两个三角形才能保证全等呢?
三条边对应相等,三个角对应相等.
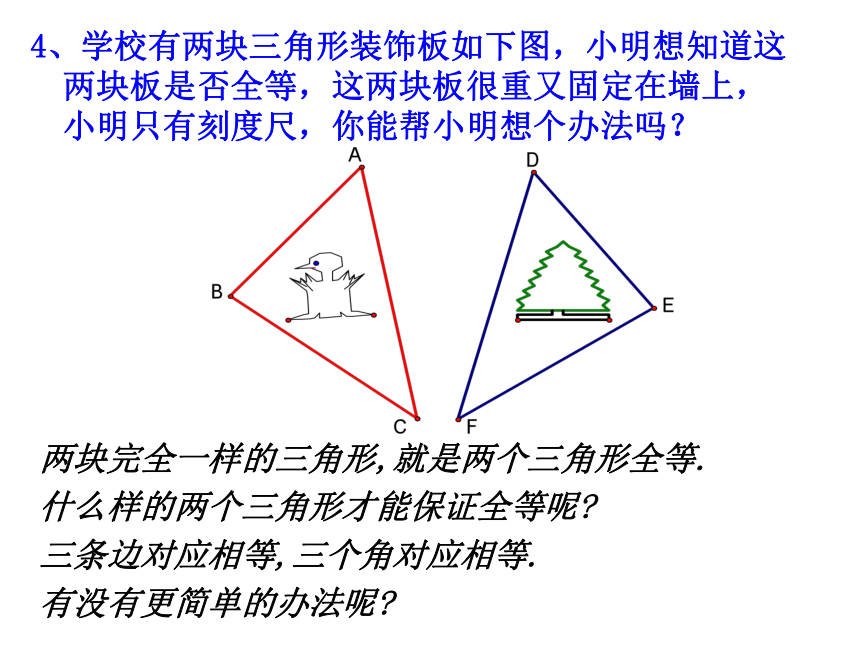
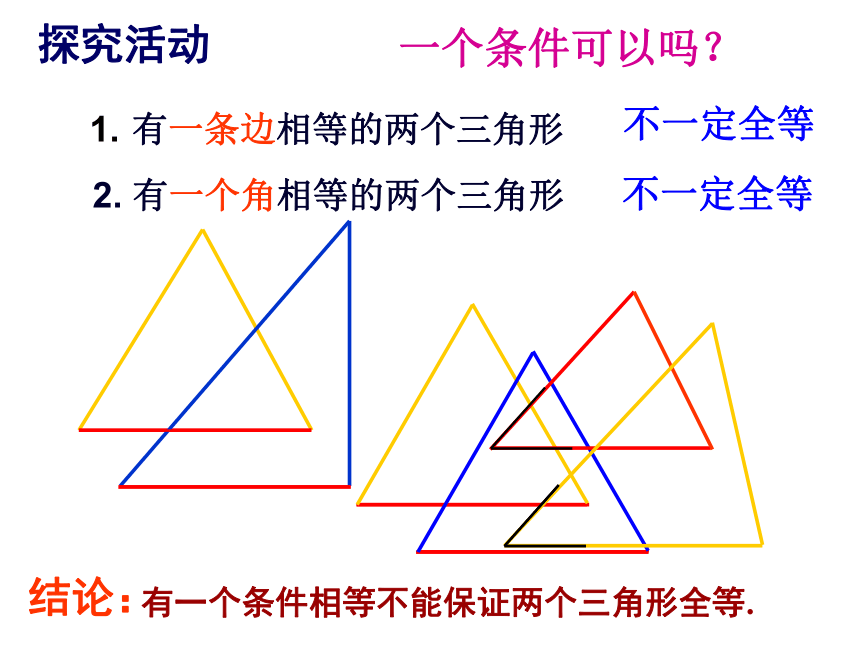
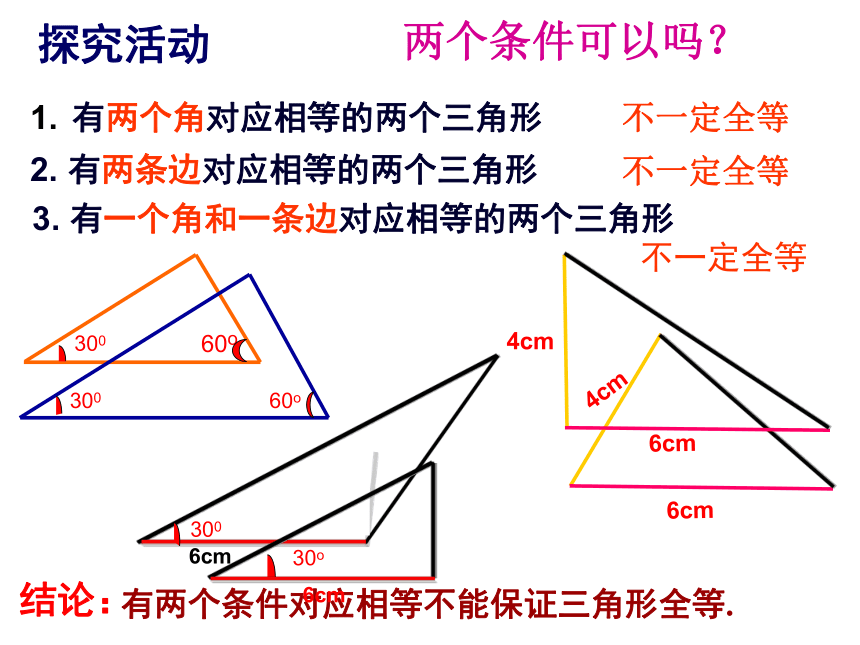
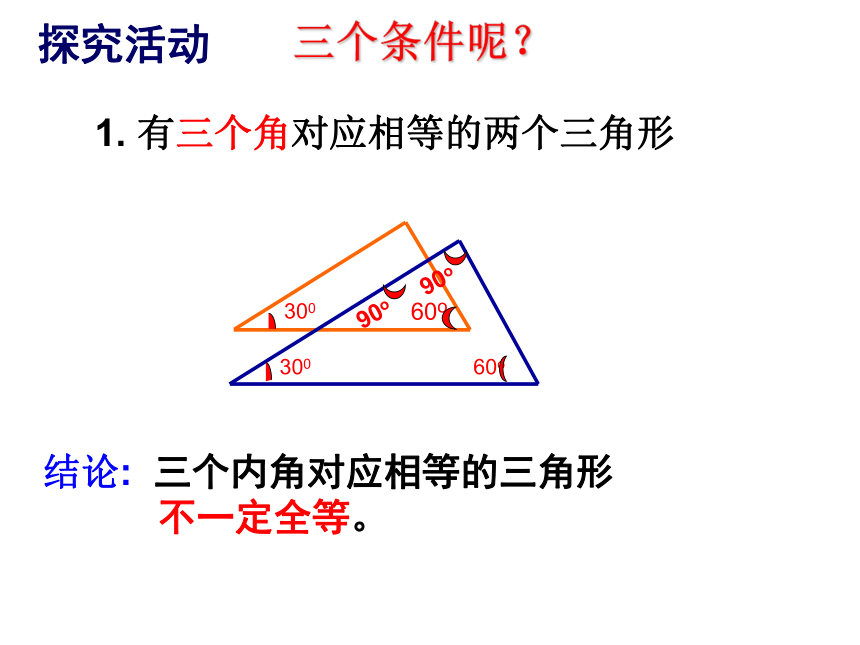
有没有更简单的办法呢?4、学校有两块三角形装饰板如下图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?探索三角形全等的条件只给一个条件一个条件可以吗? 有一条边相等的两个三角形不一定全等探究活动2. 有一个角相等的两个三角形不一定全等结论:有一个条件相等不能保证两个三角形全等.有两个条件对应相等不能保证三角形全等.不一定全等 有两个角对应相等的两个三角形两个条件可以吗?3. 有一个角和一条边对应相等的两个三角形2. 有两条边对应相等的两个三角形不一定全等不一定全等结论:探究活动三个条件呢?探究活动
三个角;2. 三条边;3. 两边一角;4. 两角一边。如果给出三个条件画三角形,
你能说出有哪几种可能的情况?结论: 三个内角对应相等的三角形
不一定全等。探究活动 有三个角对应相等的两个三角形三个条件呢? 阅读课本P35-37页,思考以下问题:二、问题引领:1、如何画一个三角形,与已知三角形的三边对应相等?
2、在本节中,你得到的三角形全等的判定方法是什么?
3、结合例1总结求证三角形全等的思路以及表达格式。
4、如何做一个角等于已知角?利用的是什么原理?若已知一个三角形的三条边,你能画出这个三角形吗?三边对应相等的两个三角形会全等吗?动手试一试探究活动 作法:1、画线段A′B′=AB;
2、分别以A′、B′为圆心,以线段AC、BC为半径作弧,两弧交于点C′;
3、连接线段B′C′,A′C′.A′B′C′三、问题释疑:1、探究:三角形全等的判定方法“边边边”(1)先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA,把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?(2)画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?画法: 1.画线段AB=3㎝;2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;3. 连接线段AC、BC.结论 三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。用上面的结论可以判定两个三角形全等. 判断两个三角形全等的推理过程,叫做证明三角形全等.例1 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边{①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:例2 如图,△ABC是一个钢架,AB=AC,
AD是连接点A与BC中点D的支架.
求证: △ABD≌△ACD.ABCD应用迁移,巩固提高(1)(2)∠BAD = ∠CAD.(2)由(1)得△ABD≌△ACD ,
∴ ∠BAD= ∠CAD.
(全等三角形对应角相等)例、已知:∠AOB,
求作:∠A′O′B′,使∠A′O′B′=∠AOBOABCDO′A′B′C′D′作法:1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
4、过点D′画射线O′B′。
则∠A′O′B′即为所求。 工人师傅常用角尺平分一个任意角. 做法如下:如图,AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合. 过角尺顶点C的射线OC便是AOB的平分线.为什么?练习课 本 P37≌(全等三角形对应角相等)(已知)(已知)(公共边) 小明做了一个如图所示的风筝,他想去验证∠BAC与∠DAC是否相等,但手头却只有一把足够长的尺子。你能帮助他想个方法吗?说明你这样做的理由。思考?思考? 已知AC=FE,BC=DE,点A、D、 B、
F在一条直线上,AD=FB. 要用“边边边”证明
△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,
还应该有AB=DF这个条件∵AD=FB
∴ AD+DB=FB+DB
即 AB=FD思考? 已知AC=FE,BC=DE,点A、D、 B、
F在一条直线上,AD=FB. 要用“边边边”证明
△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?练习1:如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?解:有三组。
在△ABH和△ACH中,
∵AB=AC,BH=CH,AH=AH,
∴△ABH≌△ACH(SSS); 在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS);在△DBH和△DCH中
∵BD=CD,BH=CH,DH=DH,
∴△DBH≌△DCH(SSS).(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件 .BCBC△DCBBF=DC或 BD=FCABCD练习2解: △ABC≌△DCB
理由如下:
AB = DC
AC = DB
=
△ABC≌ ( ) SSS(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 AE B D F C
练习3、如图,在四边形ABCD中, AB=CD, AD=CB, 求证:∠ A= ∠ C. 证明:在△ABD和△CDB中AB=CDAD=CBBD=DB∴△ABD≌△CDB(SSS)(已知)(已知)(公共边)∴ ∠ A=∠C (全等三角形的对应角相等)你能说明AB∥CD,AD∥BC吗?请同学们谈谈本节课的收获与体会本节课你学到了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题? 小 结2. 三边对应相等的两个三角形全等
(简写成“边边边” 或“SSS”);1. 知道三角形三条边的长度怎样画三角形;3. 初步学会理解证明的思路,
应用“边边边”证明两个三角形全等.作业:
1、P43-44第1、9题
2、笔记补充完整Over!
(第1课时)一、知识回顾 1. 什么叫全等三角形?能够完全重合的两个三角形叫 全等三角形。2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等≌两块完全一样的三角形,就是两个三角形全等.
什么样的两个三角形才能保证全等呢?
三条边对应相等,三个角对应相等.
有没有更简单的办法呢?4、学校有两块三角形装饰板如下图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?探索三角形全等的条件只给一个条件一个条件可以吗? 有一条边相等的两个三角形不一定全等探究活动2. 有一个角相等的两个三角形不一定全等结论:有一个条件相等不能保证两个三角形全等.有两个条件对应相等不能保证三角形全等.不一定全等 有两个角对应相等的两个三角形两个条件可以吗?3. 有一个角和一条边对应相等的两个三角形2. 有两条边对应相等的两个三角形不一定全等不一定全等结论:探究活动三个条件呢?探究活动
三个角;2. 三条边;3. 两边一角;4. 两角一边。如果给出三个条件画三角形,
你能说出有哪几种可能的情况?结论: 三个内角对应相等的三角形
不一定全等。探究活动 有三个角对应相等的两个三角形三个条件呢? 阅读课本P35-37页,思考以下问题:二、问题引领:1、如何画一个三角形,与已知三角形的三边对应相等?
2、在本节中,你得到的三角形全等的判定方法是什么?
3、结合例1总结求证三角形全等的思路以及表达格式。
4、如何做一个角等于已知角?利用的是什么原理?若已知一个三角形的三条边,你能画出这个三角形吗?三边对应相等的两个三角形会全等吗?动手试一试探究活动 作法:1、画线段A′B′=AB;
2、分别以A′、B′为圆心,以线段AC、BC为半径作弧,两弧交于点C′;
3、连接线段B′C′,A′C′.A′B′C′三、问题释疑:1、探究:三角形全等的判定方法“边边边”(1)先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA,把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?(2)画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?画法: 1.画线段AB=3㎝;2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;3. 连接线段AC、BC.结论 三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。用上面的结论可以判定两个三角形全等. 判断两个三角形全等的推理过程,叫做证明三角形全等.例1 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边{①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:例2 如图,△ABC是一个钢架,AB=AC,
AD是连接点A与BC中点D的支架.
求证: △ABD≌△ACD.ABCD应用迁移,巩固提高(1)(2)∠BAD = ∠CAD.(2)由(1)得△ABD≌△ACD ,
∴ ∠BAD= ∠CAD.
(全等三角形对应角相等)例、已知:∠AOB,
求作:∠A′O′B′,使∠A′O′B′=∠AOBOABCDO′A′B′C′D′作法:1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
4、过点D′画射线O′B′。
则∠A′O′B′即为所求。 工人师傅常用角尺平分一个任意角. 做法如下:如图,AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合. 过角尺顶点C的射线OC便是AOB的平分线.为什么?练习课 本 P37≌(全等三角形对应角相等)(已知)(已知)(公共边) 小明做了一个如图所示的风筝,他想去验证∠BAC与∠DAC是否相等,但手头却只有一把足够长的尺子。你能帮助他想个方法吗?说明你这样做的理由。思考?思考? 已知AC=FE,BC=DE,点A、D、 B、
F在一条直线上,AD=FB. 要用“边边边”证明
△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,
还应该有AB=DF这个条件∵AD=FB
∴ AD+DB=FB+DB
即 AB=FD思考? 已知AC=FE,BC=DE,点A、D、 B、
F在一条直线上,AD=FB. 要用“边边边”证明
△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?练习1:如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?解:有三组。
在△ABH和△ACH中,
∵AB=AC,BH=CH,AH=AH,
∴△ABH≌△ACH(SSS); 在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS);在△DBH和△DCH中
∵BD=CD,BH=CH,DH=DH,
∴△DBH≌△DCH(SSS).(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件 .BCBC△DCBBF=DC或 BD=FCABCD练习2解: △ABC≌△DCB
理由如下:
AB = DC
AC = DB
=
△ABC≌ ( ) SSS(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 AE B D F C
练习3、如图,在四边形ABCD中, AB=CD, AD=CB, 求证:∠ A= ∠ C. 证明:在△ABD和△CDB中AB=CDAD=CBBD=DB∴△ABD≌△CDB(SSS)(已知)(已知)(公共边)∴ ∠ A=∠C (全等三角形的对应角相等)你能说明AB∥CD,AD∥BC吗?请同学们谈谈本节课的收获与体会本节课你学到了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题? 小 结2. 三边对应相等的两个三角形全等
(简写成“边边边” 或“SSS”);1. 知道三角形三条边的长度怎样画三角形;3. 初步学会理解证明的思路,
应用“边边边”证明两个三角形全等.作业:
1、P43-44第1、9题
2、笔记补充完整Over!
