12.2直角三角形全等的判定课件
图片预览



文档简介
课件27张PPT。
12.2.4全等三角形判定 H L旧知回顾判断两个三角形全等的方法
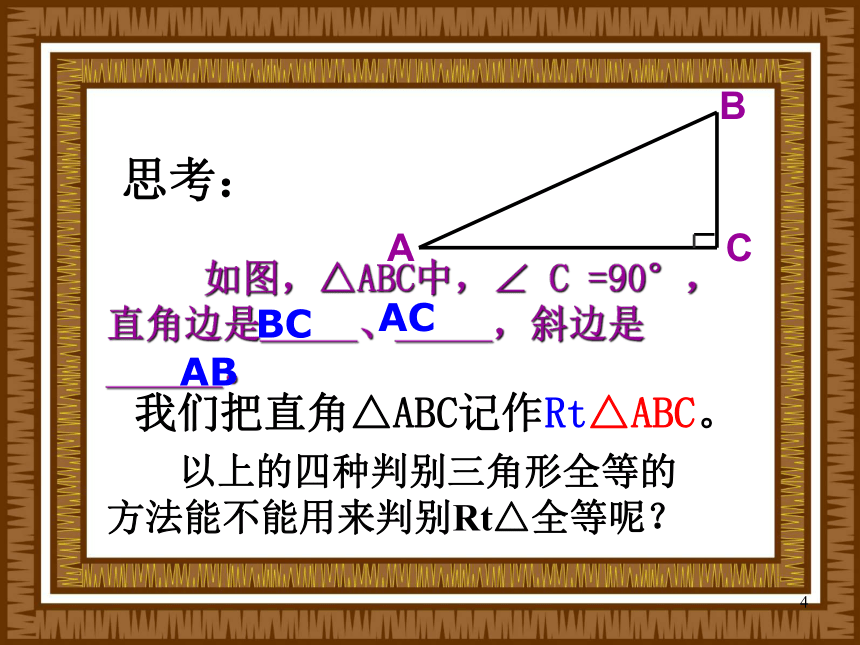
我们已经学了哪些呢?2SSSSASASAAAS3 如图,△ABC中,∠ C =90°,直角边是_____、_____,斜边是______。我们把直角△ABC记作Rt△ABC。ACBCAB 以上的四种判别三角形全等的
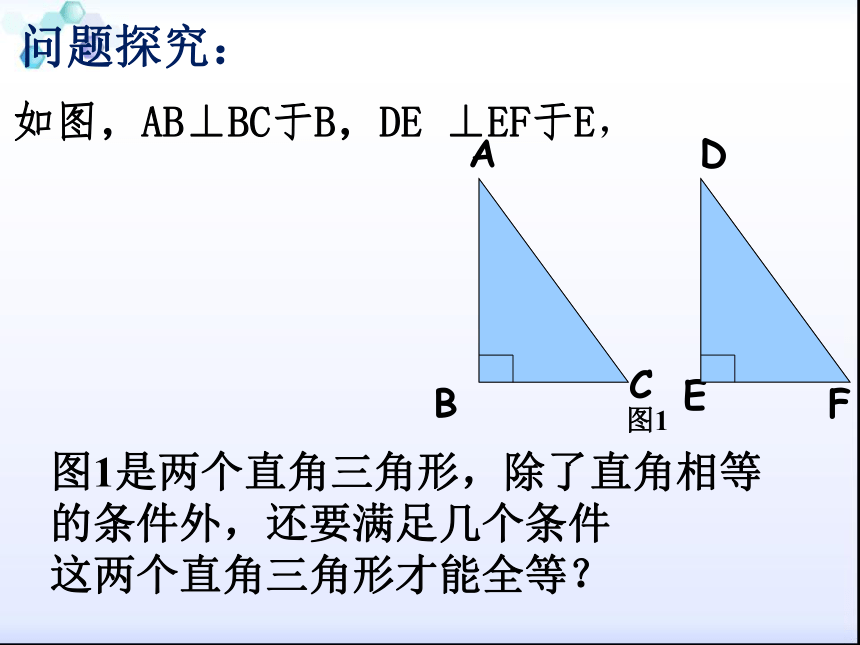
方法能不能用来判别Rt△全等呢?思考:4如图,AB⊥BC于B,DE ⊥EF于E,FBCAED图1图1是两个直角三角形,除了直角相等的条件外,还要满足几个条件
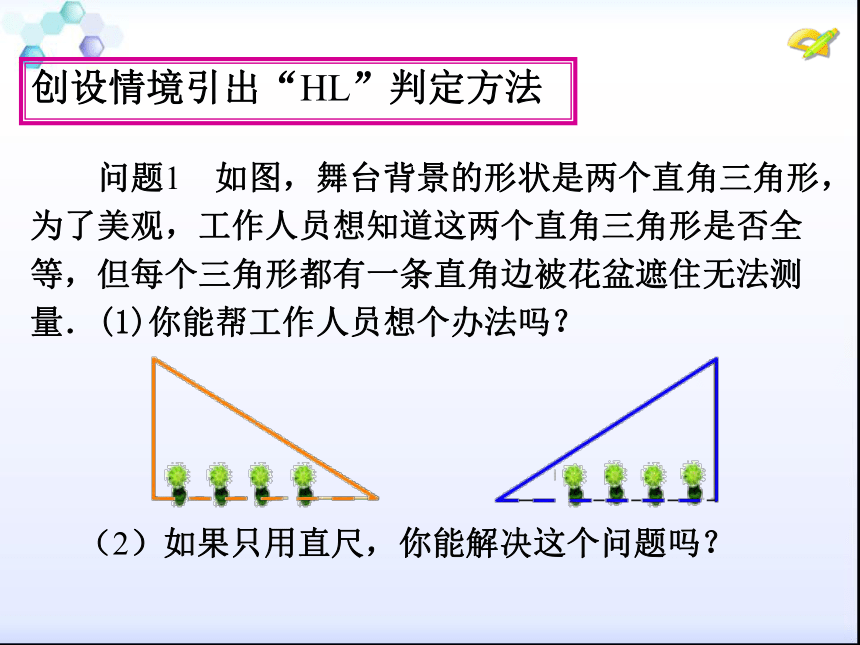
这两个直角三角形才能全等?问题探究: 问题1 如图,舞台背景的形状是两个直角三角形,
为了美观,工作人员想知道这两个直角三角形是否全
等,但每个三角形都有一条直角边被花盆遮住无法测
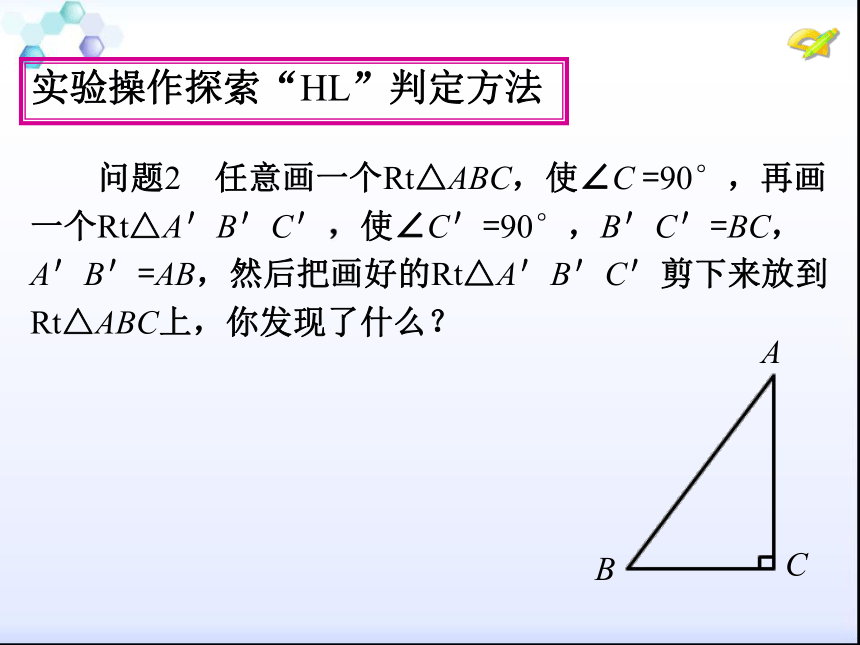
量.(1)你能帮工作人员想个办法吗?创设情境引出“HL”判定方法 (2)如果只用直尺,你能解决这个问题吗? 问题2 任意画一个Rt△ABC,使∠C =90°,再画
一个Rt△A'B'C',使∠C'=90°,B'C'=BC,
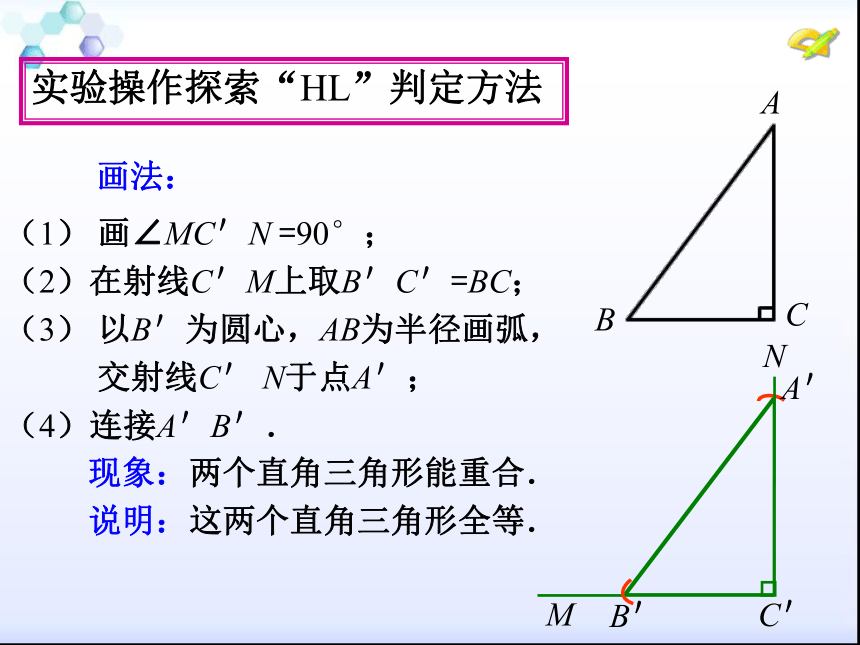
A'B'=AB,然后把画好的Rt△A'B'C'剪下来放到
Rt△ABC上,你发现了什么?实验操作探索“HL”判定方法(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'.实验操作探索“HL”判定方法 现象:两个直角三角形能重合.
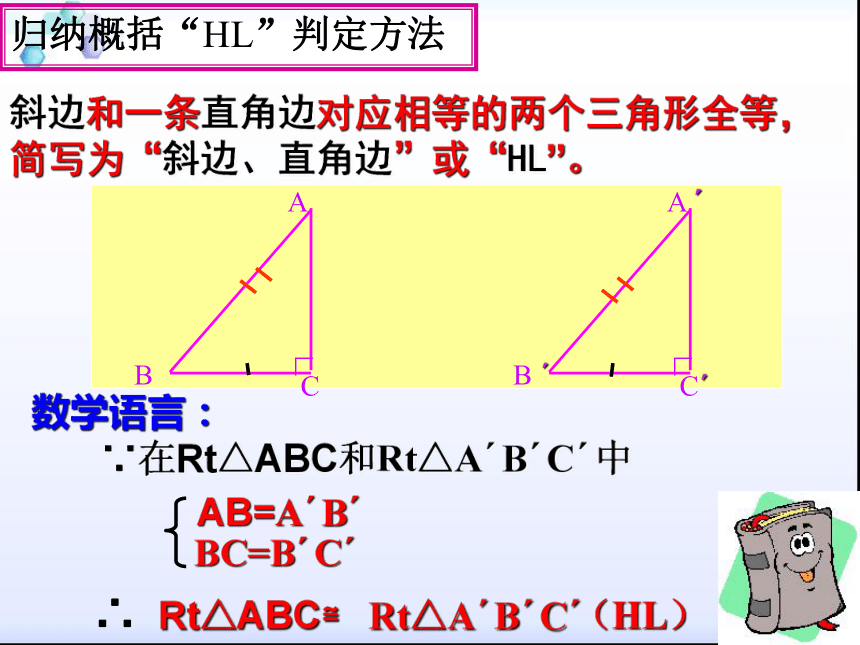
说明:这两个直角三角形全等. 画法:斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt△A′B′C′中(HL)BC=B′C′归纳概括“HL”判定方法有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”定理或“HL”直角三角形全等的判定定理高、直角边
斜边斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等。简写成“斜边、直角边”或“HL”
s前提条件1条件2例1已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.BDC证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)A证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D =90°
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).“HL”判定方法的运用例2 如图,AC⊥BC,BD⊥AD,AC =BD.
求证:BC =AD.“HL”判定方法的运用例3 如图,有两个长度相同的滑梯,左边滑梯的
高度AC 与右边滑梯水平方向的长度DF 相等,两个
滑梯 的倾斜角∠ABC 和∠DFE的大小有什么关系?为什么?∠ABC +∠DFE =90° 1.如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF162.如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CADABCD等腰三角形三线合一3.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,
D、E与路段AB的距离相等吗?为什么?CD 与CE 相等吗?证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(全等三角形对应边相等)194.如图,在 △ABC 中,BD=CD, DE⊥AB,
DF⊥AC,E、F为垂足,DE=DF,
求证: (1)△BED≌△CFD.(2)求证:△ABC是等腰三角形。(2)证明 :∵△BED≌△CFD
∴ ∠B=∠C ∴AB=AC
5.已知:如图,在△ABC和△DEF中,
AP、DQ分别是高,并且AB=DE,AP=DQ,
∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ∠BAC=∠EDF, AB=DE,∠B=∠E分析: △ABC≌△DEFRt△ABP≌Rt△DEQAB=DE,AP=DQ证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中AB=DEAP=DQ∴Rt△ABP≌Rt△DEQ (HL)
∴ ∠B=∠E
在△ABC和△DEF中∠BAC=∠EDF
AB=DE
∠B=∠E∴△ABC≌△DEF (ASA)已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF思维拓展已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。小结已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。思维拓展小结已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。思维拓展小结“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等应用“ SSS ”27祝同学们习学愉快!
我们已经学了哪些呢?2SSSSASASAAAS3 如图,△ABC中,∠ C =90°,直角边是_____、_____,斜边是______。我们把直角△ABC记作Rt△ABC。ACBCAB 以上的四种判别三角形全等的
方法能不能用来判别Rt△全等呢?思考:4如图,AB⊥BC于B,DE ⊥EF于E,FBCAED图1图1是两个直角三角形,除了直角相等的条件外,还要满足几个条件
这两个直角三角形才能全等?问题探究: 问题1 如图,舞台背景的形状是两个直角三角形,
为了美观,工作人员想知道这两个直角三角形是否全
等,但每个三角形都有一条直角边被花盆遮住无法测
量.(1)你能帮工作人员想个办法吗?创设情境引出“HL”判定方法 (2)如果只用直尺,你能解决这个问题吗? 问题2 任意画一个Rt△ABC,使∠C =90°,再画
一个Rt△A'B'C',使∠C'=90°,B'C'=BC,
A'B'=AB,然后把画好的Rt△A'B'C'剪下来放到
Rt△ABC上,你发现了什么?实验操作探索“HL”判定方法(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'.实验操作探索“HL”判定方法 现象:两个直角三角形能重合.
说明:这两个直角三角形全等. 画法:斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt△A′B′C′中(HL)BC=B′C′归纳概括“HL”判定方法有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”定理或“HL”直角三角形全等的判定定理高、直角边
斜边斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等。简写成“斜边、直角边”或“HL”
s前提条件1条件2例1已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.BDC证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)A证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D =90°
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).“HL”判定方法的运用例2 如图,AC⊥BC,BD⊥AD,AC =BD.
求证:BC =AD.“HL”判定方法的运用例3 如图,有两个长度相同的滑梯,左边滑梯的
高度AC 与右边滑梯水平方向的长度DF 相等,两个
滑梯 的倾斜角∠ABC 和∠DFE的大小有什么关系?为什么?∠ABC +∠DFE =90° 1.如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF162.如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CADABCD等腰三角形三线合一3.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,
D、E与路段AB的距离相等吗?为什么?CD 与CE 相等吗?证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(全等三角形对应边相等)194.如图,在 △ABC 中,BD=CD, DE⊥AB,
DF⊥AC,E、F为垂足,DE=DF,
求证: (1)△BED≌△CFD.(2)求证:△ABC是等腰三角形。(2)证明 :∵△BED≌△CFD
∴ ∠B=∠C ∴AB=AC
5.已知:如图,在△ABC和△DEF中,
AP、DQ分别是高,并且AB=DE,AP=DQ,
∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ∠BAC=∠EDF, AB=DE,∠B=∠E分析: △ABC≌△DEFRt△ABP≌Rt△DEQAB=DE,AP=DQ证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中AB=DEAP=DQ∴Rt△ABP≌Rt△DEQ (HL)
∴ ∠B=∠E
在△ABC和△DEF中∠BAC=∠EDF
AB=DE
∠B=∠E∴△ABC≌△DEF (ASA)已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF思维拓展已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。小结已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。思维拓展小结已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。思维拓展小结“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等应用“ SSS ”27祝同学们习学愉快!
