23.1锐角三角函数 课件
图片预览





文档简介
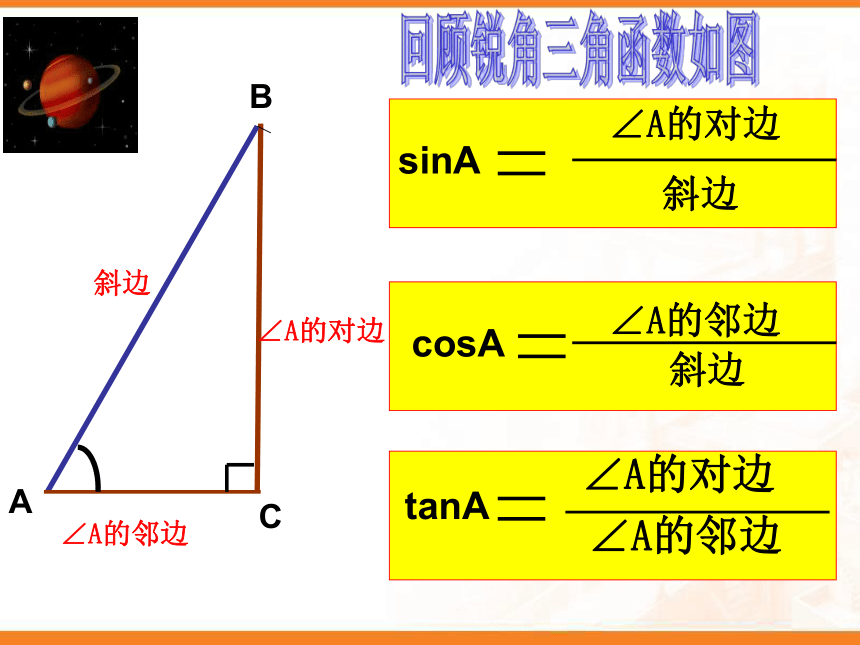
课件17张PPT。23.1 锐角三角函数 AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边斜边回顾锐角三角函数如图互余两角之间的三角函数关:
sinA=cosB,tanA.tanB=1. 同角之间的三角函数关系:
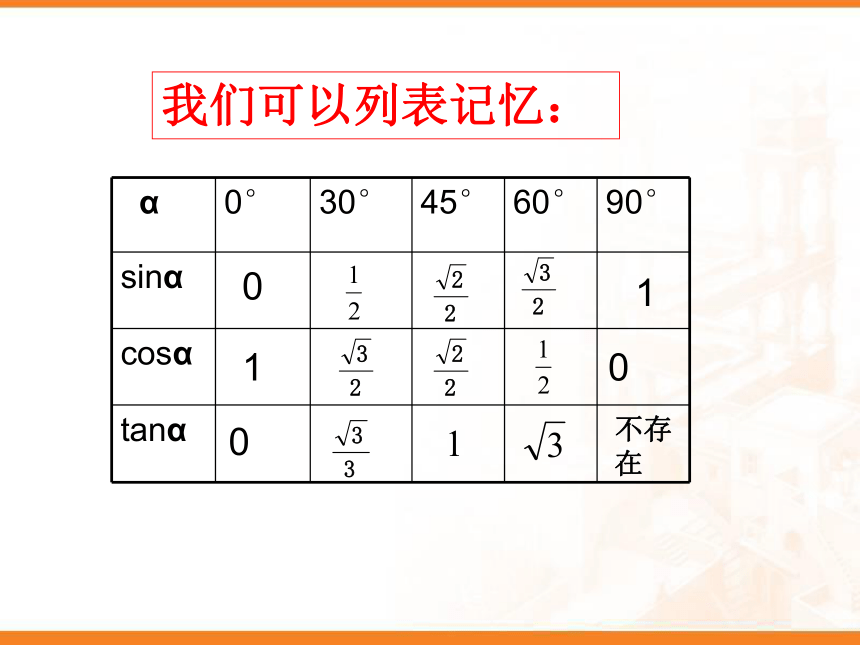
sin2A+cos2A=1.tanA=特殊角300,450,600角的三角函数值.我们可以列表记忆:01100不存在同学们,前面我们学习了特殊角30°45°60°的三角函数值,一些非特殊角
(如17°56°89°等)的三角函数值又怎么求呢?这一节课我们就学习 借助计算器 来完成这个任务.1.求已知锐角的三角函数值:例1.求sin63°52′41″的值(精确到0.0001)解按下列顺序依次按键:显示结果为0.897 859 012.所以 sin63゜52′41″≈0.8979二.新课引入练习:1.使用计算器求下列三角函数值.(精确到0.0001)
sin24゜,cos51゜42′20″,tan70゜21′.答案:sin24°=0.4060, cos51°42′20″=0.6197,tan70°21′=2.8006,SHIFT20917.301507834sin·7=已知三角函数值求角度,要用到sin,Cos,tan的第二功能键“sin-1 Cos-1,tan-1”键例如:已知sinα=0.2974,求锐角α.按健顺序为:如果再按“度分秒健”就换算成度分秒,°′″即∠ α=17o18’5.43”2已知锐角的三角函数值,求角度:例2,根据下面的条件,求锐角β的大小(精确到1)
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036
按键盘顺序如下:26048’51”0.sin115=4SHIFT°′″即∠ β =26048’51”1.用计算器求下式的值.(精确到0.0001)sin81°32′17″+cos38°43′47″答案:1.76922.已知tanA=3.1748,利用计算器求 锐角A.(精确到1′)答案:∠A≈72°52′练习:3.比较大小:cos30° cos60°,
tan30° tan60°.答案 : ﹥, ﹤4.已知锐角a的三角函数值,使用计算器求锐角x (精确到1′)
(1)sin a=0.2476; (2)cos a=0.4
(3)tan a=0.1890; 答案: (1)α≈14°20′;(3)α≈10°42′;(2)α≈65°20′;练习:☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围1. 当 锐角A>45°时,sinA的值( )B2. 当锐角A>30°时,cosA的值( )C☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°3. 当∠A为锐角,且tanA的值大于 时,∠A( )B4. 确定角的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°C☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围4. 确定角的范围(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° (A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° DA例3、一段公路弯道呈弧形,测得弯道
AB两端的距离为200米,AB 的半径为1000米,求弯道的长(精确到0.1米)⌒⌒ABOR谈谈今天的收获畅所欲言
sinA=cosB,tanA.tanB=1. 同角之间的三角函数关系:
sin2A+cos2A=1.tanA=特殊角300,450,600角的三角函数值.我们可以列表记忆:01100不存在同学们,前面我们学习了特殊角30°45°60°的三角函数值,一些非特殊角
(如17°56°89°等)的三角函数值又怎么求呢?这一节课我们就学习 借助计算器 来完成这个任务.1.求已知锐角的三角函数值:例1.求sin63°52′41″的值(精确到0.0001)解按下列顺序依次按键:显示结果为0.897 859 012.所以 sin63゜52′41″≈0.8979二.新课引入练习:1.使用计算器求下列三角函数值.(精确到0.0001)
sin24゜,cos51゜42′20″,tan70゜21′.答案:sin24°=0.4060, cos51°42′20″=0.6197,tan70°21′=2.8006,SHIFT20917.301507834sin·7=已知三角函数值求角度,要用到sin,Cos,tan的第二功能键“sin-1 Cos-1,tan-1”键例如:已知sinα=0.2974,求锐角α.按健顺序为:如果再按“度分秒健”就换算成度分秒,°′″即∠ α=17o18’5.43”2已知锐角的三角函数值,求角度:例2,根据下面的条件,求锐角β的大小(精确到1)
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036
按键盘顺序如下:26048’51”0.sin115=4SHIFT°′″即∠ β =26048’51”1.用计算器求下式的值.(精确到0.0001)sin81°32′17″+cos38°43′47″答案:1.76922.已知tanA=3.1748,利用计算器求 锐角A.(精确到1′)答案:∠A≈72°52′练习:3.比较大小:cos30° cos60°,
tan30° tan60°.答案 : ﹥, ﹤4.已知锐角a的三角函数值,使用计算器求锐角x (精确到1′)
(1)sin a=0.2476; (2)cos a=0.4
(3)tan a=0.1890; 答案: (1)α≈14°20′;(3)α≈10°42′;(2)α≈65°20′;练习:☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围1. 当 锐角A>45°时,sinA的值( )B2. 当锐角A>30°时,cosA的值( )C☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°3. 当∠A为锐角,且tanA的值大于 时,∠A( )B4. 确定角的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°C☆ 应用练习1.已知角,求值2.已知值,求角3. 确定值的范围4. 确定角的范围(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° (A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 ° DA例3、一段公路弯道呈弧形,测得弯道
AB两端的距离为200米,AB 的半径为1000米,求弯道的长(精确到0.1米)⌒⌒ABOR谈谈今天的收获畅所欲言
