21.2二次函数的图像和性质 课件
图片预览


文档简介
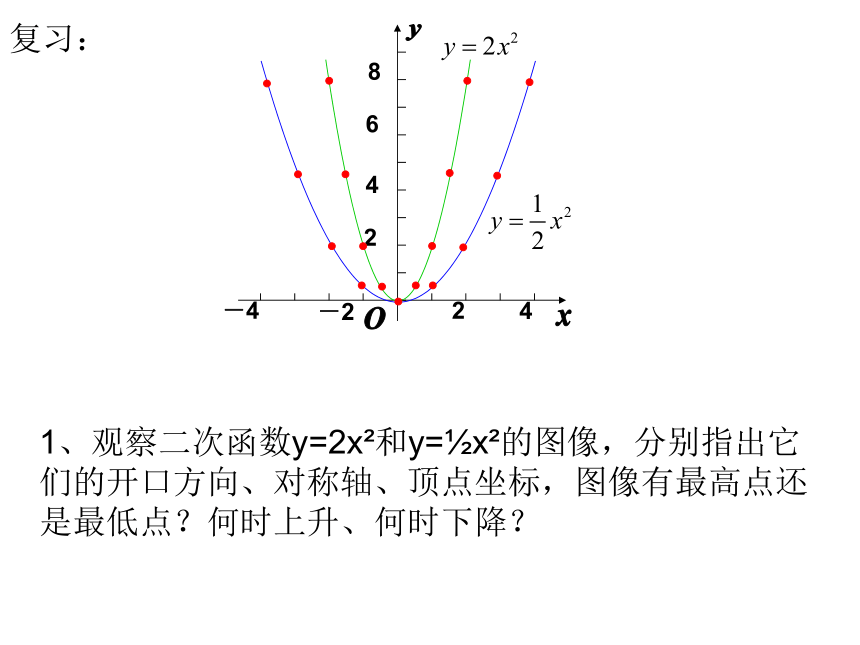
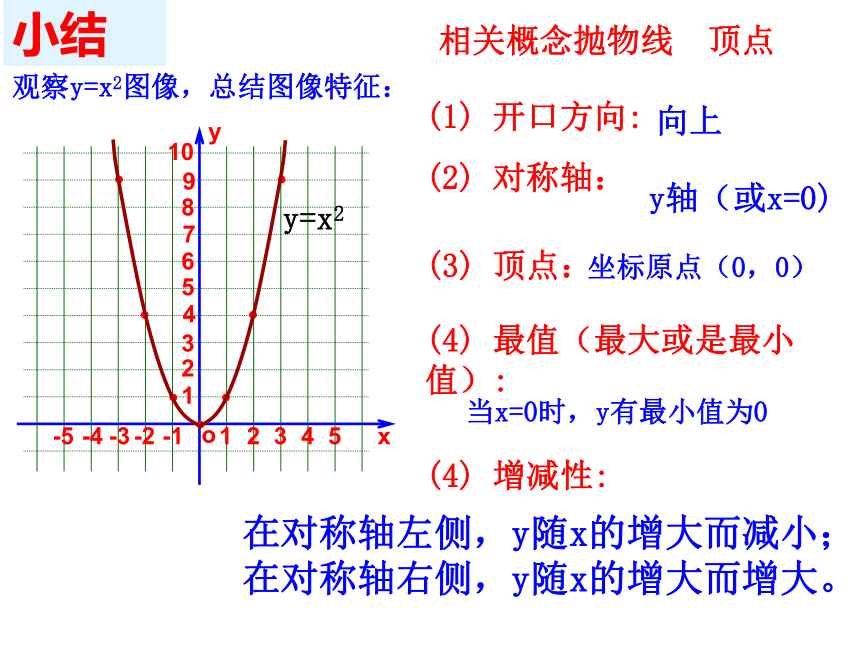
课件14张PPT。二次函数y=ax2的图像和性质2xyoy=ax2(a>0)y=ax2(a<0)1、观察二次函数y=2x2和y=?x2的图像,分别指出它们的开口方向、对称轴、顶点坐标,图像有最高点还是最低点?何时上升、何时下降?复习:相同点:开口都向上,顶点是原点而且是抛物线的最低点,对称轴是 y 轴不同点:a 越大,抛物线的开口越小.观察y=x2图像,总结图像特征:y=x2小结相关概念抛物线 顶点(2) 对称轴:(3) 顶点:(1) 开口方向: (4) 增减性:(4) 最值(最大或是最小值):向上y轴(或x=0)坐标原点(0,0)当x=0时,y有最小值为0在对称轴左侧,y随x的增大而减小;
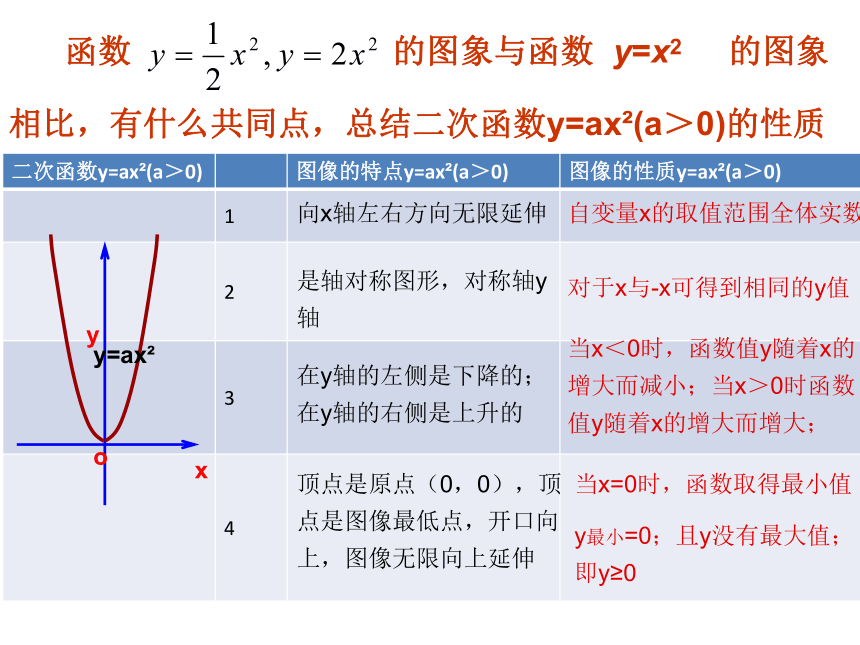
在对称轴右侧,y随x的增大而增大。自变量x的取值范围全体实数向x轴左右方向无限延伸自变量x的取值范围全体实数是轴对称图形,对称轴y轴对于x与-x可得到相同的y值在y轴的左侧是下降的;在y轴的右侧是上升的当x<0时,函数值y随着x的增大而减小;当x>0时函数值y随着x的增大而增大;顶点是原点(0,0),顶点是图像最低点,开口向上,图像无限向上延伸当x=0时,函数取得最小值
y最小=0;且y没有最大值;即y≥0 在同一坐标系内作出函数
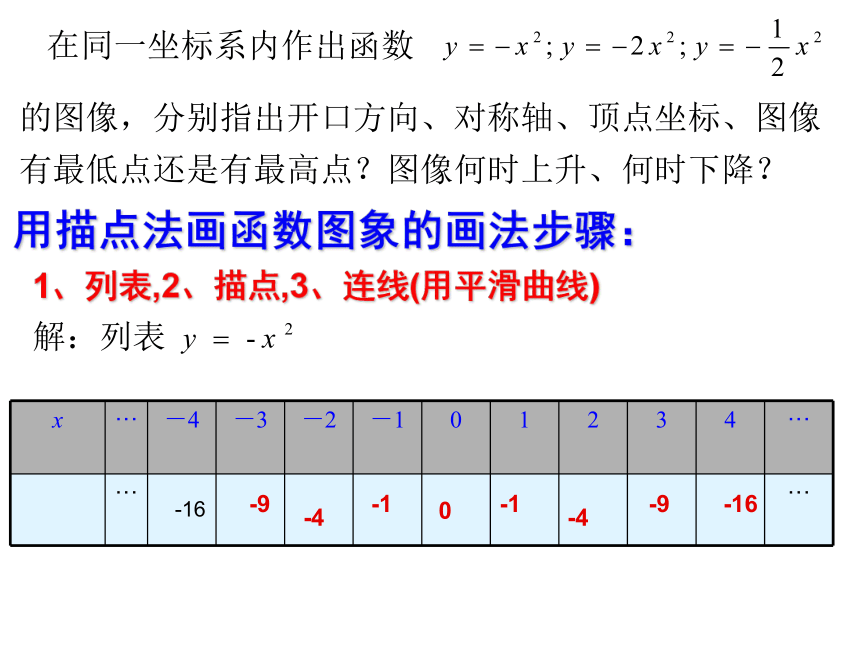
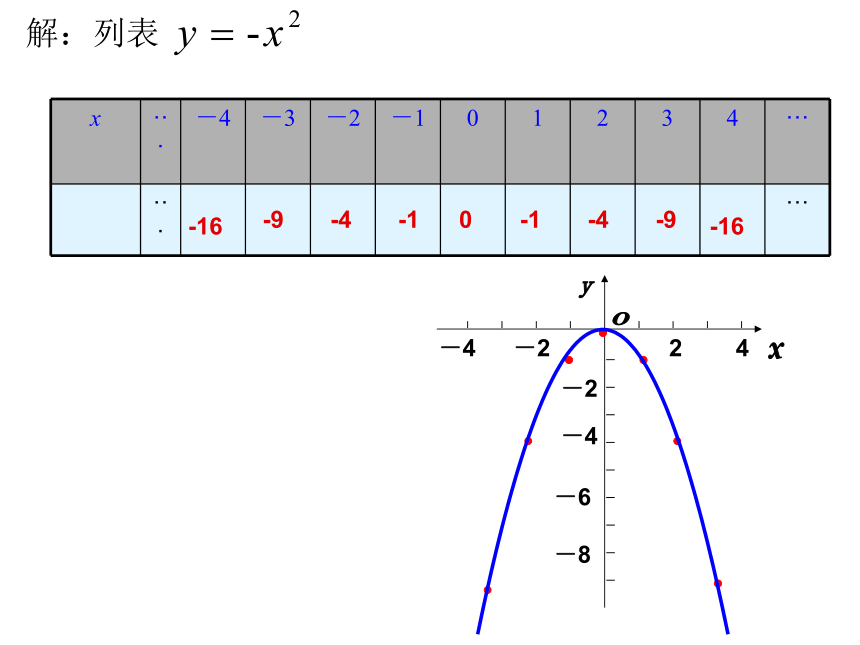
的图像,分别指出开口方向、对称轴、顶点坐标、图像有最低点还是有最高点?图像何时上升、何时下降?解:列表用描点法画函数图象的画法步骤:1、列表,2、描点,3、连线(用平滑曲线)0-1-4-9-16-1-4-9-16解:列表0-1-1-4-4-9-9-16-16-8-4.5-2-0.50-8-4.5-2-0.5-8-4.5-2-0.50-8-4.5-2-0.5自变量x的取值范围全体实数向x轴左右方向无限延伸自变量x的取值范围全体实数是轴对称图形,对称轴y轴对于x与-x可得到相同的y值在y轴的左侧是上升的;在y轴的右侧是下降的当x<0时,函数值y随着x的增大而增大;当x>0时函数值y随着x的增大而减小;顶点是原点(0,0),顶点是图像最高点,开口向下,图像无限向下延伸当x=0时,函数取得最大值
y最大=0;且y没有最小值;即y≤0相同点:开口都向下,顶点是原点而且是抛物线的最高点,对称轴是 y 轴 不同点:IaI越大,抛物线的开口越小.(1)比较函数y=x2与y=-x2、y=?x2与y=-?x2、y=2x2与y=-2x2的图像,指出它们的相同与不同;(2)思考以下内容,并回答:
(1)a>0与a<0时,y=ax2的图像有什么不同?
(2) IaI的大小对于y=ax2的图像2有什么影响?思考: a的符号决定抛物线的开口方向,|a|的大小决定抛物线开口的大小,|a|越大开口越小2.抛物线y=ax2与y=-ax2关于____对称,关于原点中心对称3、|a| 越大,抛物线的开口越_____, 反之,|a| 越小,抛物线的开口越 .1、抛物线y=ax2的性质:归纳向下向上(0,0)(0,0)y轴(x=0 )y轴当x>0时,y随x的增大而 增大,当x<0时, y随x的增大而减小. 当x>0时,y随x的增大而 减小,当x<0时, y随x的增大而增大. 0000小大x轴越小越大(x=0 )同学们再见!同学们再见!作业:练习 1、2
在对称轴右侧,y随x的增大而增大。自变量x的取值范围全体实数向x轴左右方向无限延伸自变量x的取值范围全体实数是轴对称图形,对称轴y轴对于x与-x可得到相同的y值在y轴的左侧是下降的;在y轴的右侧是上升的当x<0时,函数值y随着x的增大而减小;当x>0时函数值y随着x的增大而增大;顶点是原点(0,0),顶点是图像最低点,开口向上,图像无限向上延伸当x=0时,函数取得最小值
y最小=0;且y没有最大值;即y≥0 在同一坐标系内作出函数
的图像,分别指出开口方向、对称轴、顶点坐标、图像有最低点还是有最高点?图像何时上升、何时下降?解:列表用描点法画函数图象的画法步骤:1、列表,2、描点,3、连线(用平滑曲线)0-1-4-9-16-1-4-9-16解:列表0-1-1-4-4-9-9-16-16-8-4.5-2-0.50-8-4.5-2-0.5-8-4.5-2-0.50-8-4.5-2-0.5自变量x的取值范围全体实数向x轴左右方向无限延伸自变量x的取值范围全体实数是轴对称图形,对称轴y轴对于x与-x可得到相同的y值在y轴的左侧是上升的;在y轴的右侧是下降的当x<0时,函数值y随着x的增大而增大;当x>0时函数值y随着x的增大而减小;顶点是原点(0,0),顶点是图像最高点,开口向下,图像无限向下延伸当x=0时,函数取得最大值
y最大=0;且y没有最小值;即y≤0相同点:开口都向下,顶点是原点而且是抛物线的最高点,对称轴是 y 轴 不同点:IaI越大,抛物线的开口越小.(1)比较函数y=x2与y=-x2、y=?x2与y=-?x2、y=2x2与y=-2x2的图像,指出它们的相同与不同;(2)思考以下内容,并回答:
(1)a>0与a<0时,y=ax2的图像有什么不同?
(2) IaI的大小对于y=ax2的图像2有什么影响?思考: a的符号决定抛物线的开口方向,|a|的大小决定抛物线开口的大小,|a|越大开口越小2.抛物线y=ax2与y=-ax2关于____对称,关于原点中心对称3、|a| 越大,抛物线的开口越_____, 反之,|a| 越小,抛物线的开口越 .1、抛物线y=ax2的性质:归纳向下向上(0,0)(0,0)y轴(x=0 )y轴当x>0时,y随x的增大而 增大,当x<0时, y随x的增大而减小. 当x>0时,y随x的增大而 减小,当x<0时, y随x的增大而增大. 0000小大x轴越小越大(x=0 )同学们再见!同学们再见!作业:练习 1、2
