21.5反比例函数图象与性质(课件)
图片预览




文档简介
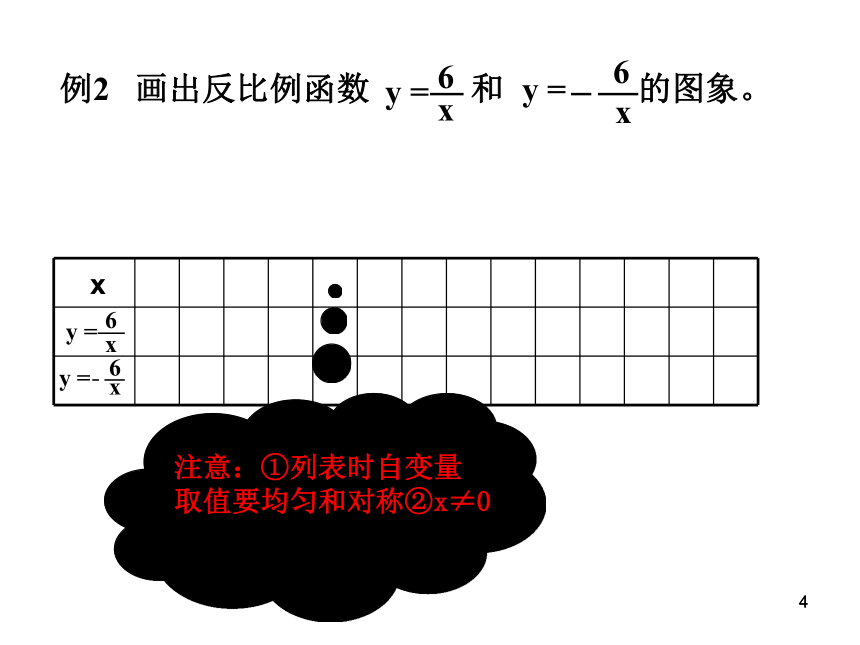
课件17张PPT。21.5 反比例函数(第2课时) 反比例函数的图象和性质 2016.9.2411知识回顾1、什么是反比例函数? 2、反比例函数的定义中还需要注意什么?◆自变量x的取值范围◆自变量x的次数为-2 (k是常数,k≠0)-1x≠0◆若函数y=(m-2)xm2-5是反比例函数,则m= , 11研究反比例函数的图象和性质1、列表2、描点3、连线画函数图象的一般步骤:11注意:①列表时自变量
取值要均匀和对称②x≠0
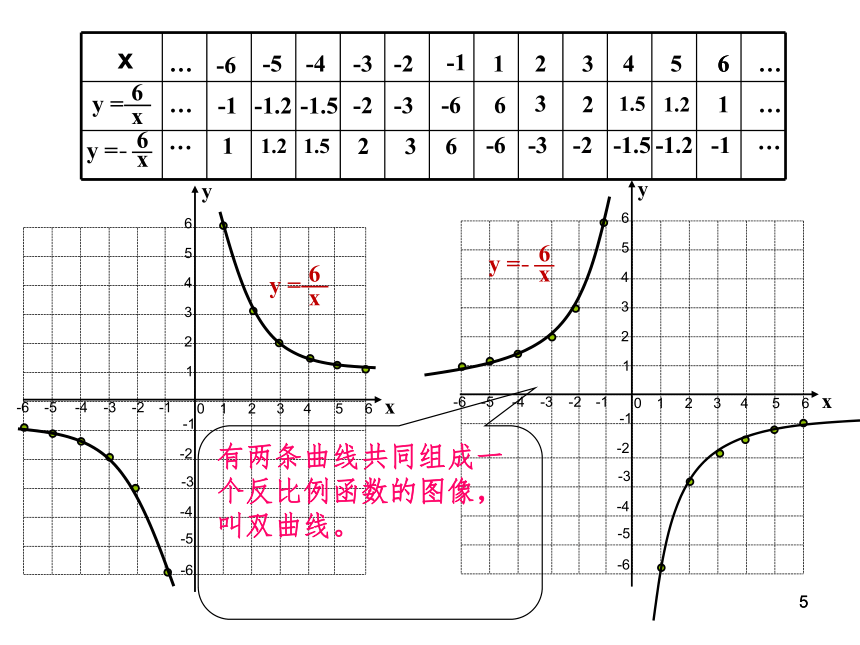
11123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……有两条曲线共同组成一个反比例函数的图像,叫双曲线。 113.当k>0时,双曲线两分支各在哪个象限?在每个象限内, 随着自变量x的增大,函数值y如何变化?请大家结合反比例函数 和 的函数图象,围绕以下问题分析反比例函数的性质。 04.当k<0呢?1.它和两条坐标轴的位置关系是怎样的?2. 反比例函数 ,具有怎样的对称性?11在每个象限内在每个象限内yXOk>0K<0反比例函数的图象和性质双曲线的两支分别双曲线的两支分别双曲线k>0k<0位于第一、第三象限,位于第二、第四象限,y值随x值的增大而减小.y值随x值的增大而增大.1、反比例函数 (k为常数,k≠0)
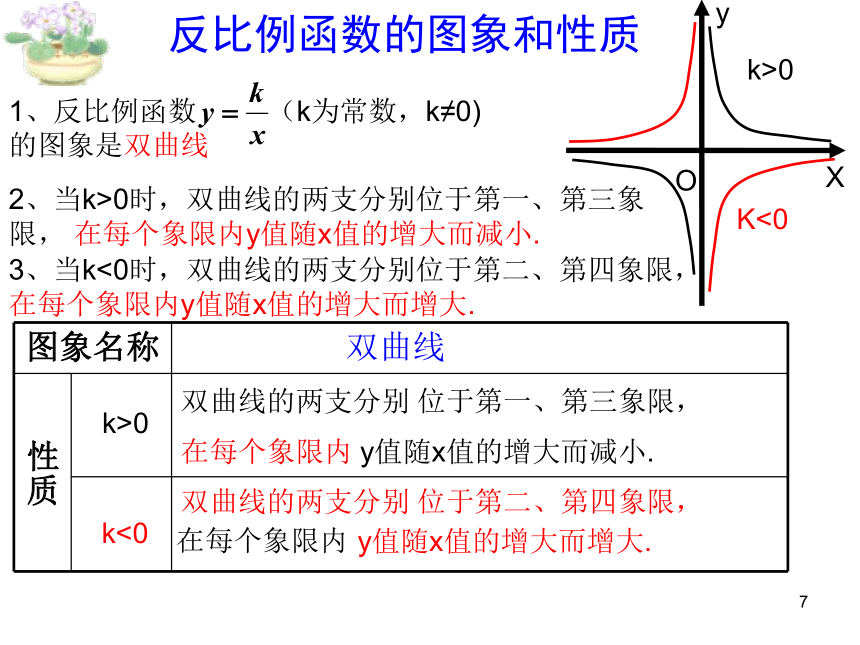
的图象是双曲线2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小.3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大.1位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限在每个象限内 y随x的增大而减小二四象限二四象限 y随x的增大而减小在每个象限内 y随x的增大而增大
填表分析正比例函数和反比例函数的区别比一比11例3:已知反比例函数y=
(1)如果这个函数图象经过点(-3,5),求k值;
(2)如果这个函数图象在它所处的象限内,函数y随x的增大而减小,求k的范围.例题解析11(1)对于函数 ,自变量 x的取值范围是
____,当x >0时,y___0;当x <0时,y___0.
(2)对于函数 ,当x >0时,函数y随x的增大而_____ ;当x < 0时,函数y随x的增大而_____ . (3)反比例函数 的图象与直线y=2x交于两点,这两点的坐标分别是(__ , __ )和(__ , __ ).
练习1.填空1x≠0 < > 增大增大21-1-21议一议: 已知点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线 于点A,过点A作AB⊥y轴于B点。在点P运动过程中,矩形OPAB
的面积是否发生变化?
若不变,请求出其面积;
若改变,试说明理由。1K的几何意义:=OA·AP=|m| ·|n|=|k|1 如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ 。变式一:1
练习2.P为反比例函数 图象上的一个点,作PQ垂直于x轴,垂足为Q.问△OPQ的面积是否会因点P位置的变化而变化,为什么?1POQxyB1 如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______变式二:(A)s=1 (B) s=2
(C)1(1)分布情况
(2)对称性
(3)增减性
(4)面积不变性11作业必做题:教材第49页5,6选做题:教材第50页9名校课堂:第35页至36页
第2课时 反比例函数的图象和性质1
取值要均匀和对称②x≠0
11123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……有两条曲线共同组成一个反比例函数的图像,叫双曲线。 113.当k>0时,双曲线两分支各在哪个象限?在每个象限内, 随着自变量x的增大,函数值y如何变化?请大家结合反比例函数 和 的函数图象,围绕以下问题分析反比例函数的性质。 04.当k<0呢?1.它和两条坐标轴的位置关系是怎样的?2. 反比例函数 ,具有怎样的对称性?11在每个象限内在每个象限内yXOk>0K<0反比例函数的图象和性质双曲线的两支分别双曲线的两支分别双曲线k>0k<0位于第一、第三象限,位于第二、第四象限,y值随x值的增大而减小.y值随x值的增大而增大.1、反比例函数 (k为常数,k≠0)
的图象是双曲线2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小.3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大.1位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限在每个象限内 y随x的增大而减小二四象限二四象限 y随x的增大而减小在每个象限内 y随x的增大而增大
填表分析正比例函数和反比例函数的区别比一比11例3:已知反比例函数y=
(1)如果这个函数图象经过点(-3,5),求k值;
(2)如果这个函数图象在它所处的象限内,函数y随x的增大而减小,求k的范围.例题解析11(1)对于函数 ,自变量 x的取值范围是
____,当x >0时,y___0;当x <0时,y___0.
(2)对于函数 ,当x >0时,函数y随x的增大而_____ ;当x < 0时,函数y随x的增大而_____ . (3)反比例函数 的图象与直线y=2x交于两点,这两点的坐标分别是(__ , __ )和(__ , __ ).
练习1.填空1x≠0 < > 增大增大21-1-21议一议: 已知点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线 于点A,过点A作AB⊥y轴于B点。在点P运动过程中,矩形OPAB
的面积是否发生变化?
若不变,请求出其面积;
若改变,试说明理由。1K的几何意义:=OA·AP=|m| ·|n|=|k|1 如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ 。变式一:1
练习2.P为反比例函数 图象上的一个点,作PQ垂直于x轴,垂足为Q.问△OPQ的面积是否会因点P位置的变化而变化,为什么?1POQxyB1 如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______变式二:(A)s=1 (B) s=2
(C)1
(2)对称性
(3)增减性
(4)面积不变性11作业必做题:教材第49页5,6选做题:教材第50页9名校课堂:第35页至36页
第2课时 反比例函数的图象和性质1
