21.6综合与实践获取最大利润课件
图片预览





文档简介
课件19张PPT。21.6综合与实践获取最大利润九(1)是我家,我爱我家!复习(1)二次函数y=-10x2+80x+200,顶点坐标为________;当x= 时,函数有最 值为 .
(2) 某产品进货单价为90元,按100元一个售出时,能售500个,如果这种商品涨价1元,其销售额就减少10个,为了获得最大利润,其单价应定为( )
A.130元; B.120元
C.110元; D.100元获取最大利润在日常生活、生产和科研中,常常会遇到求什么条件下可使面积最大、利润最大、材料最省、时间最少、效率最高等问题,这类问题称为最优化问题。其中一些问题可以归结为求二次函数的最大值或最小值。
看课本P52页内容!问题① 当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路。一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降。假设某市场分析专家提供了下列数据: 设生产t件该产品的成本为
C=50t+1000完成下列要求 (1)在下图中,描出上述表格中的各组数据对应的点;050100150200250300350x/元10002000300040005000t/件(2)描出的这些点在一条直线上吗?求t和x之间的函数表达式;
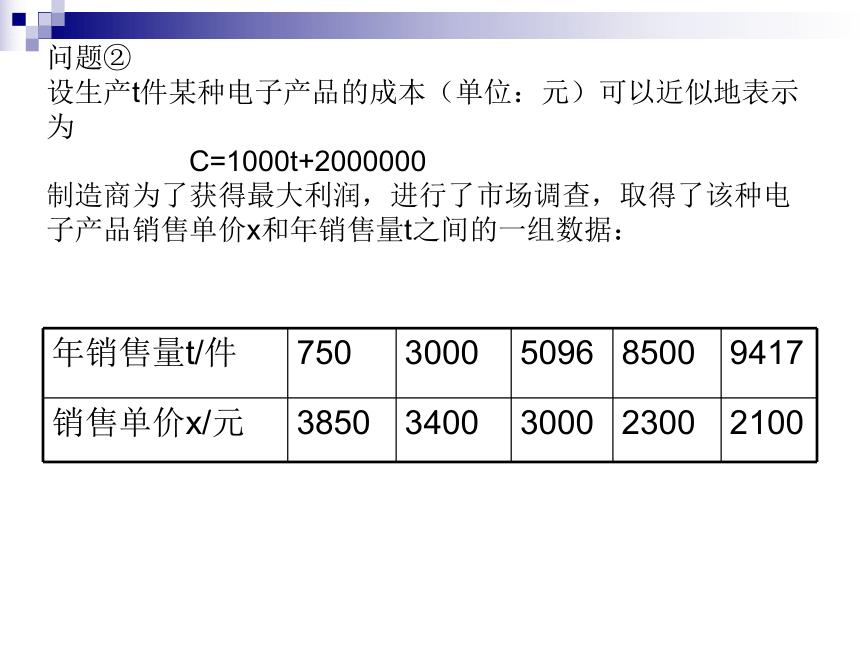
(3)问当销售单价x和年销售量t各为多少时,年利润最大?问题② 设生产t件某种电子产品的成本(单位:元)可以近似地表示为 C=1000t+2000000 制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据:(1)在下图中,描出上述表格中各组数据对应的点;01000200030004000500060007000800090001000020002500300035004000t/件x/元(2)请你帮助制造商分析,当年销售量t和销售单价x分别是多少时,年利润P最大?并说说你有几种求解的方法?
与同学们进行交流!问题③某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式. (2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少? (3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?练习1.某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每天销售量w(件)与销售单价x(元)之间的关系可近似的看作一次函数: .设李明每天获得利润为y(元),当销售单价定为多少元时,每天可获得最大利润?2.某公司生产的A种产品,它的成本是2元,售价是3元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(10万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:(1)求y与x的函数表达式; (2)如果把利润看作是销售总额减去成本和广告费,试写出年利润S(10万元)与广告费x(10万元)函数表达式; (3)如果投入的广告费为10万元~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?课堂小结1、这节课我们学习了什么?
2、你收获了哪些知识?
3、你还有哪些困惑的地方?
4、课后你需要辅导吗?
5、你的收获和困惑,你愿意和你的同伴分 享吗?作业看课本P52—54页,了解本节课的知识结构。
(2) 某产品进货单价为90元,按100元一个售出时,能售500个,如果这种商品涨价1元,其销售额就减少10个,为了获得最大利润,其单价应定为( )
A.130元; B.120元
C.110元; D.100元获取最大利润在日常生活、生产和科研中,常常会遇到求什么条件下可使面积最大、利润最大、材料最省、时间最少、效率最高等问题,这类问题称为最优化问题。其中一些问题可以归结为求二次函数的最大值或最小值。
看课本P52页内容!问题① 当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路。一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降。假设某市场分析专家提供了下列数据: 设生产t件该产品的成本为
C=50t+1000完成下列要求 (1)在下图中,描出上述表格中的各组数据对应的点;050100150200250300350x/元10002000300040005000t/件(2)描出的这些点在一条直线上吗?求t和x之间的函数表达式;
(3)问当销售单价x和年销售量t各为多少时,年利润最大?问题② 设生产t件某种电子产品的成本(单位:元)可以近似地表示为 C=1000t+2000000 制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据:(1)在下图中,描出上述表格中各组数据对应的点;01000200030004000500060007000800090001000020002500300035004000t/件x/元(2)请你帮助制造商分析,当年销售量t和销售单价x分别是多少时,年利润P最大?并说说你有几种求解的方法?
与同学们进行交流!问题③某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式. (2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少? (3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?练习1.某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每天销售量w(件)与销售单价x(元)之间的关系可近似的看作一次函数: .设李明每天获得利润为y(元),当销售单价定为多少元时,每天可获得最大利润?2.某公司生产的A种产品,它的成本是2元,售价是3元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(10万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:(1)求y与x的函数表达式; (2)如果把利润看作是销售总额减去成本和广告费,试写出年利润S(10万元)与广告费x(10万元)函数表达式; (3)如果投入的广告费为10万元~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?课堂小结1、这节课我们学习了什么?
2、你收获了哪些知识?
3、你还有哪些困惑的地方?
4、课后你需要辅导吗?
5、你的收获和困惑,你愿意和你的同伴分 享吗?作业看课本P52—54页,了解本节课的知识结构。
