人教版八年级数学上册13.3.1等腰三角形第1课时课件
文档属性
| 名称 | 人教版八年级数学上册13.3.1等腰三角形第1课时课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 925.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-13 00:00:00 | ||
图片预览


文档简介
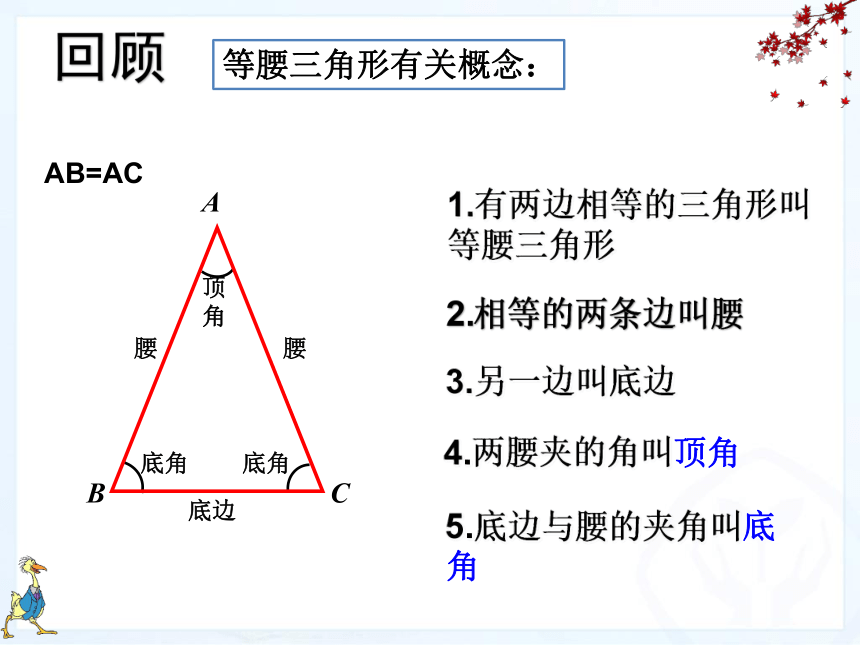
课件16张PPT。13.3.1等腰三角形腰腰底边底角顶角底角ABC回顾等腰三角形有关概念:1.有两边相等的三角形叫等腰三角形2.相等的两条边叫腰3.另一边叫底边4.两腰夹的角叫顶角5.底边与腰的夹角叫底角AB=AC学习目标
1、掌握等腰三角形的概念及性质。
2、从轴对称的角度去探索等腰三角形的性质。
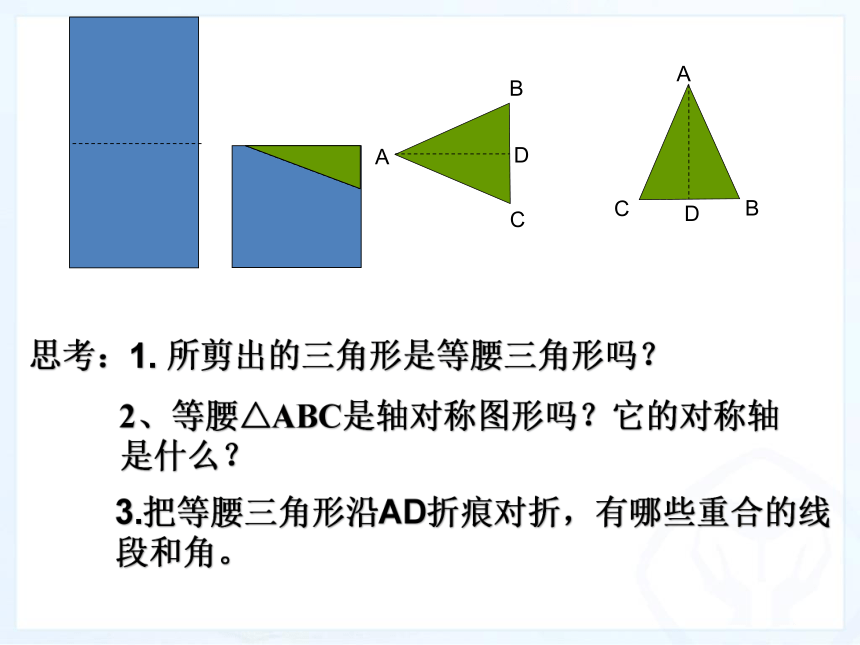
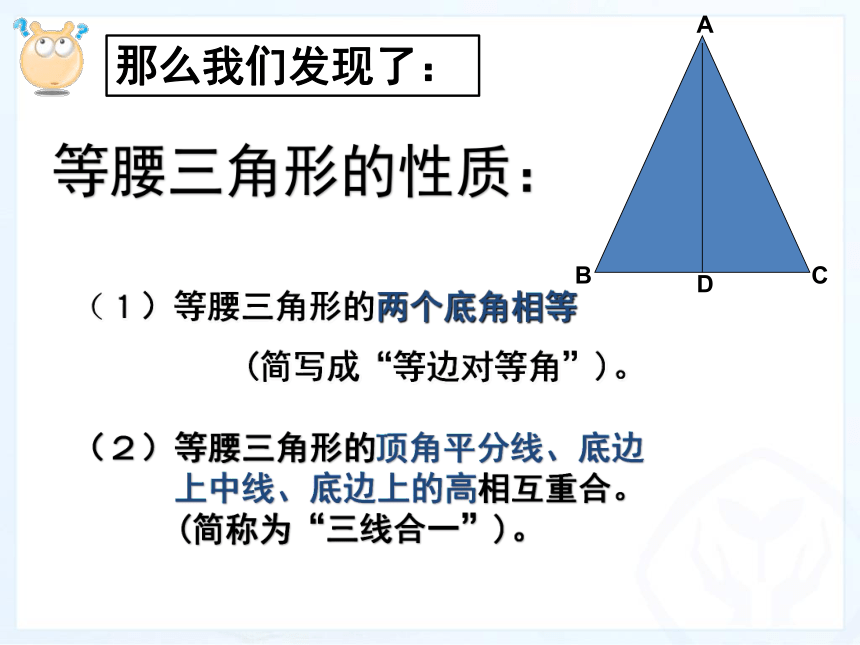
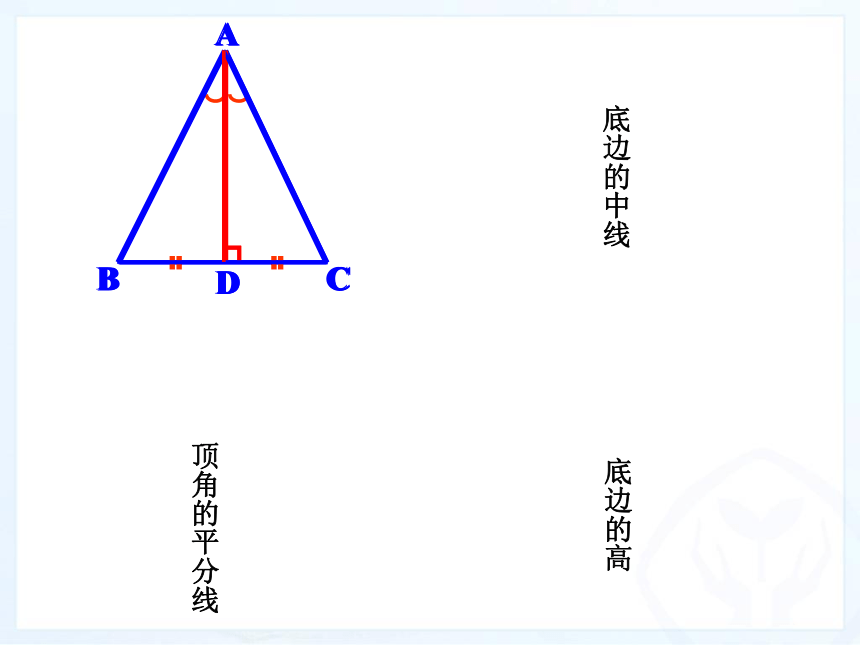
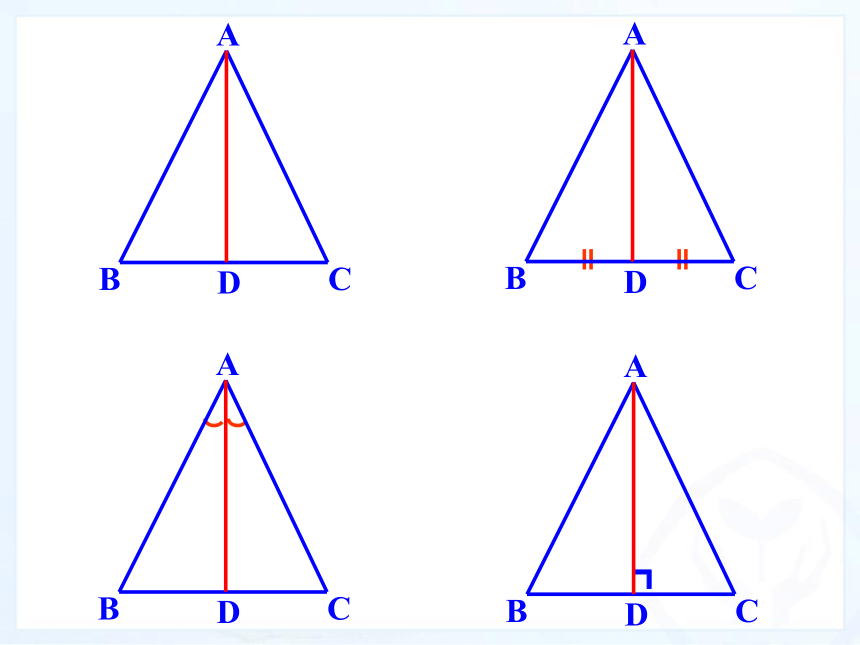
3、会运用等腰三角形性质解决简单的数学问题。ABCDABCD思考:1. 所剪出的三角形是等腰三角形吗?3.把等腰三角形沿AD折痕对折,有哪些重合的线段和角。2、等腰△ABC是轴对称图形吗?它的对称轴是什么?那么我们发现了:(1)等腰三角形的两个底角相等
(简写成“等边对等角”)。等腰三角形的性质:ABCD(2)等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合。
(简称为“三线合一”)。┓顶角的平分线底边的高底边的中线ABCD性质1:等腰三角形的两个底角相等(简写成“等边对等角”).性质1的题设和结论分别是什么?如何证明?已知:在△ABC中,AB=AC,求证:∠B=∠C证明:作底边BC的中线AD
∵AD是底边BC的中线
∴BD=CD
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD(公共边)
∴ △ ABD≌ △ACD(SSS)
∴ ∠ B = ∠ C符号语言:
∵ 在△ABC 中, AB =AC ,
∴ ∠B =∠C .等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”). 等腰三角形的性质2
等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(简写成“三线合一)。性质2可以分解为三个命题: 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:∵ AD 是底边BC 的中线,
∴ BD =CD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS)
∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.活 动1.如图,在下列等腰三角形中,分别求出它们的底角的度数。36°120°2.如图,△ABC是等腰三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、 ∠C、 ∠BAD、 ∠DAC的度数。图中有哪些相等的线段?BCAD72°72°30°30°45°45°45°45°相等的线段有:
AB=AC,AD=BD=CD 例1 如图,在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,求△ABC各角的度数. 解:
∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC(等边对等角).
∠A=∠ABD(等边对等角).
设∠A=x,则∠BDC = ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x. 于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得 x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°.ABC
5. 如图,在△ABC中,AB=AD=DC,
∠BAD=26 °,求∠ B和∠ C的度数。D
解:∵AB=AD=DC
∴∠B= ∠ ADB
∠ C= ∠ CAD(等边对等角)课 堂 小 结:等腰三角形的性质:(1)等腰三角形的两个底角相等.(简写成“等边对等角”)。
(2)等腰三角形的顶角平分线、底边上中线、底边上的高相 互重合(简写成“三线合一 ”).
同 学 们, 再 见!
1、掌握等腰三角形的概念及性质。
2、从轴对称的角度去探索等腰三角形的性质。
3、会运用等腰三角形性质解决简单的数学问题。ABCDABCD思考:1. 所剪出的三角形是等腰三角形吗?3.把等腰三角形沿AD折痕对折,有哪些重合的线段和角。2、等腰△ABC是轴对称图形吗?它的对称轴是什么?那么我们发现了:(1)等腰三角形的两个底角相等
(简写成“等边对等角”)。等腰三角形的性质:ABCD(2)等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合。
(简称为“三线合一”)。┓顶角的平分线底边的高底边的中线ABCD性质1:等腰三角形的两个底角相等(简写成“等边对等角”).性质1的题设和结论分别是什么?如何证明?已知:在△ABC中,AB=AC,求证:∠B=∠C证明:作底边BC的中线AD
∵AD是底边BC的中线
∴BD=CD
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD(公共边)
∴ △ ABD≌ △ACD(SSS)
∴ ∠ B = ∠ C符号语言:
∵ 在△ABC 中, AB =AC ,
∴ ∠B =∠C .等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”). 等腰三角形的性质2
等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(简写成“三线合一)。性质2可以分解为三个命题: 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:∵ AD 是底边BC 的中线,
∴ BD =CD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS)
∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.活 动1.如图,在下列等腰三角形中,分别求出它们的底角的度数。36°120°2.如图,△ABC是等腰三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、 ∠C、 ∠BAD、 ∠DAC的度数。图中有哪些相等的线段?BCAD72°72°30°30°45°45°45°45°相等的线段有:
AB=AC,AD=BD=CD 例1 如图,在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,求△ABC各角的度数. 解:
∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC(等边对等角).
∠A=∠ABD(等边对等角).
设∠A=x,则∠BDC = ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x. 于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得 x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°.ABC
5. 如图,在△ABC中,AB=AD=DC,
∠BAD=26 °,求∠ B和∠ C的度数。D
解:∵AB=AD=DC
∴∠B= ∠ ADB
∠ C= ∠ CAD(等边对等角)课 堂 小 结:等腰三角形的性质:(1)等腰三角形的两个底角相等.(简写成“等边对等角”)。
(2)等腰三角形的顶角平分线、底边上中线、底边上的高相 互重合(简写成“三线合一 ”).
同 学 们, 再 见!
