13.1.2线段垂直平分线的性质第1课时(人教版)课件
文档属性
| 名称 | 13.1.2线段垂直平分线的性质第1课时(人教版)课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 967.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-13 11:00:53 | ||
图片预览



文档简介
(共23张PPT)
M
N
A
B
C
A′
C′
B′
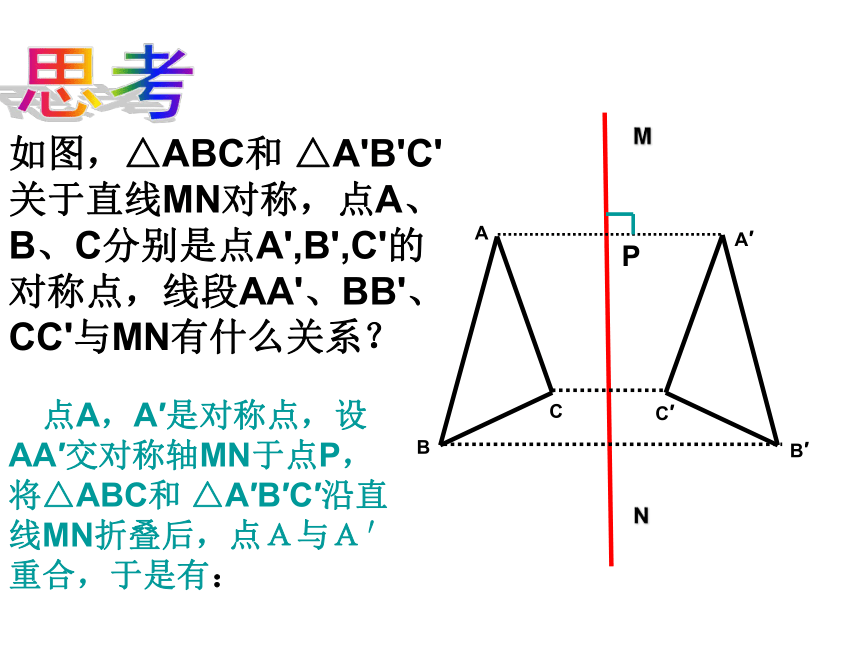
如图,△ABC和 △A'B'C'关于直线MN对称,点A、B、C分别是点A',B',C'的对称点,线段AA'、BB'、CC'与MN有什么关系?
P
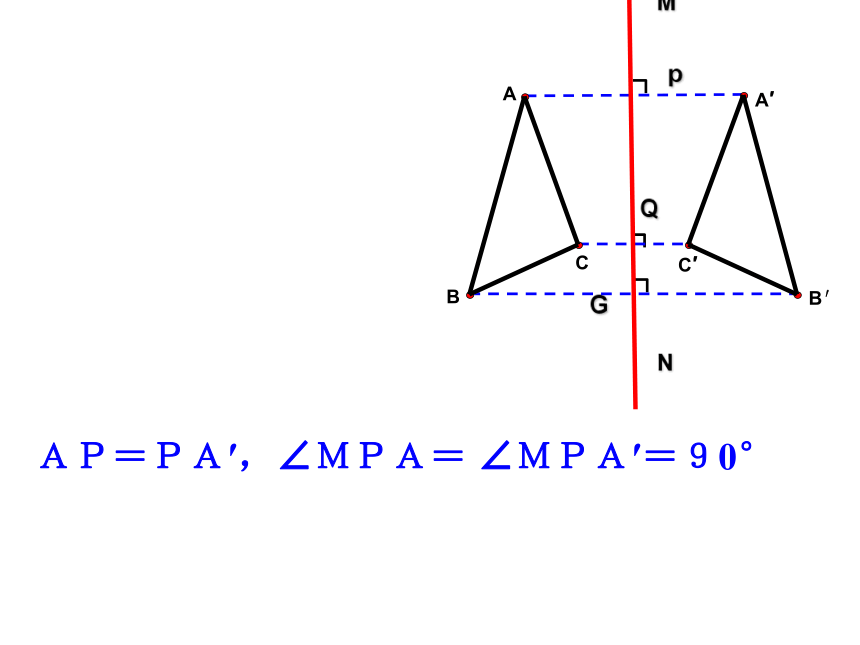
点A,A′是对称点,设AA′交对称轴MN于点P,将△ABC和 △A′B′C′沿直线MN折叠后,点A与A′重合,于是有:
AP=PA′,∠MPA= ∠MPA′=90°
M
N
Q
p
G
A
B
C
A′
C′
B′
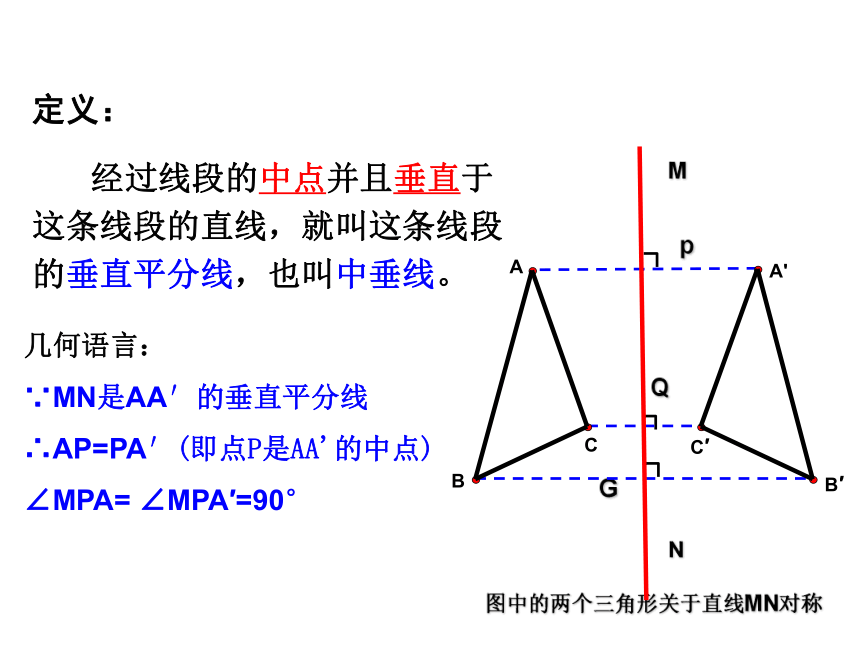
定义:
经过线段的中点并且垂直于这条线段的直线,就叫这条线段的垂直平分线,也叫中垂线。
图中的两个三角形关于直线MN对称
Q
p
G
M
N
A
B
C
A'
C′
B′
几何语言:
∵MN是AA′的垂直平分线
∴AP=PA′(即点P是AA'的中点)
∠MPA= ∠MPA′=90°
A
B
l
P1
P2
P3
P4
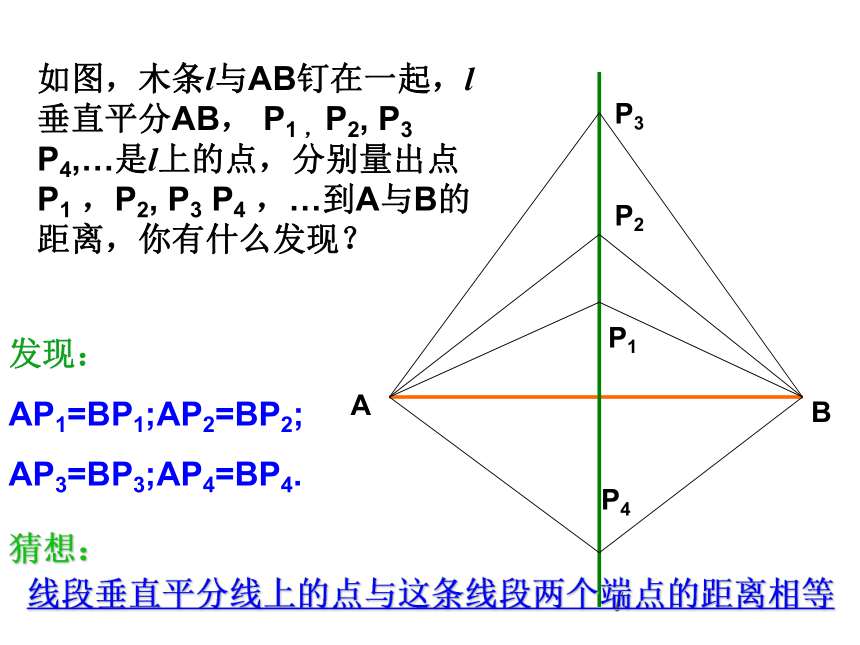
如图,木条l与AB钉在一起,l垂直平分AB, P1 ,P2, P3 P4,…是l上的点,分别量出点P1 ,P2, P3 P4 ,…到A与B的距离,你有什么发现?
发现:
AP1=BP1;AP2=BP2;
AP3=BP3;AP4=BP4.
猜想:
线段垂直平分线上的点与这条线段两个端点的距离相等
A
B
C
P
l
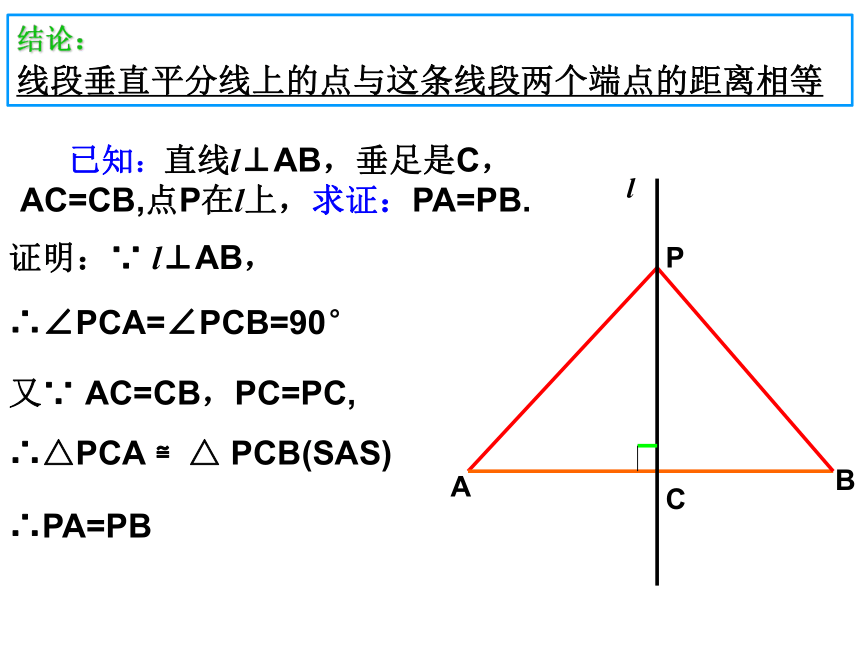
已知:直线l⊥AB,垂足是C,AC=CB,点P在l上,求证:PA=PB.
证明:∵ l⊥AB,
∴∠PCA=∠PCB=90°
又∵ AC=CB,PC=PC,
∴△PCA ≌△ PCB(SAS)
∴PA=PB
结论:
线段垂直平分线上的点与这条线段两个端点的距离相等
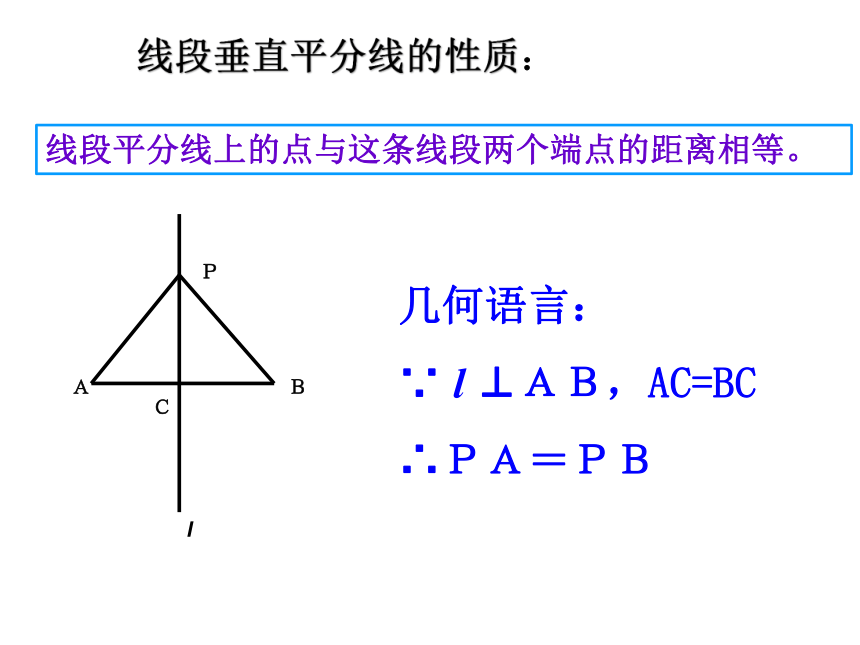
线段平分线上的点与这条线段两个端点的距离相等。
线段垂直平分线的性质:
P
A
l
C
B
几何语言:
∵ l ⊥AB,AC=BC
∴PA=PB
探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线l上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线l上.
A
B
P
C
l
探索并证明线段垂直平分线的判定
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线l上.
A
B
P
C
l
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段垂直平分线的判定:
几何语言:
∵ PA=PB
∴ 点P在AB的垂直平分线l上
A
B
P
C
l
这些点能组成什么几何图形?
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.
A
B
P
C
l
1、∵ ,∴AB=AC。
理由:
2、∵ ,∴A在线段BC的中垂线上
理由:
AD是BC的中垂线
AB=AC
线段垂直平分线上的点与这条线段两个端点的距离相等.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
B
C
A
D
3、如图, NM是线段AB的中垂线,
下列说法正确的有: 。
①AB⊥MN,②AD=DB, ③MN⊥AB, ④MD=DN,⑤AB是MN的垂直平分线
A
B
M
N
D
①②③
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
D
C
B
E
A
解:
∵ED是线段AB的垂直平分线
∴
∵ C△BCD=BD+DC+BC
∴ C△BCD=
=
=
BD=AD
AD+DC+BC
AC+BC
12+7=19
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.
课堂练习
练习3 如图,AB =AC,MB =MC.直线AM 是线段
BC 的垂直平分线吗?
A
B
C
D
M
练习2:如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
练习3:如图,与图形A成轴对称的是哪个图形?画出它们的对称轴.
练习4:如图,在Rt△ABC中,∠C=90°,AD是角平分线且AD=BD,AC=10. 求AB的长度.
提示:过点D作DE⊥AB于E
A
B
C
D
E
(1)说一说本节课我们学习了哪些内容?你有什么收获?
课堂小结
1.垂直平分线的定义:
∵MN是AB的垂直平分线
∴ , ;
2.垂直平分线的性质:
∵MN是AB的垂直平分线
∴ ( )
3.垂直平分线的判定:
∵PA=PB
∴ (
)
MN⊥AB
P
A
B
M
N
D
AD=BD
PA=PB
线段垂直平分线上点与这条线段两个端点的距离相等
P在AB的垂直平分线上
与一条线段两个端点距
离相等的点,在这条线段的垂直平分线上
M
N
A
B
C
A′
C′
B′
如图,△ABC和 △A'B'C'关于直线MN对称,点A、B、C分别是点A',B',C'的对称点,线段AA'、BB'、CC'与MN有什么关系?
P
点A,A′是对称点,设AA′交对称轴MN于点P,将△ABC和 △A′B′C′沿直线MN折叠后,点A与A′重合,于是有:
AP=PA′,∠MPA= ∠MPA′=90°
M
N
Q
p
G
A
B
C
A′
C′
B′
定义:
经过线段的中点并且垂直于这条线段的直线,就叫这条线段的垂直平分线,也叫中垂线。
图中的两个三角形关于直线MN对称
Q
p
G
M
N
A
B
C
A'
C′
B′
几何语言:
∵MN是AA′的垂直平分线
∴AP=PA′(即点P是AA'的中点)
∠MPA= ∠MPA′=90°
A
B
l
P1
P2
P3
P4
如图,木条l与AB钉在一起,l垂直平分AB, P1 ,P2, P3 P4,…是l上的点,分别量出点P1 ,P2, P3 P4 ,…到A与B的距离,你有什么发现?
发现:
AP1=BP1;AP2=BP2;
AP3=BP3;AP4=BP4.
猜想:
线段垂直平分线上的点与这条线段两个端点的距离相等
A
B
C
P
l
已知:直线l⊥AB,垂足是C,AC=CB,点P在l上,求证:PA=PB.
证明:∵ l⊥AB,
∴∠PCA=∠PCB=90°
又∵ AC=CB,PC=PC,
∴△PCA ≌△ PCB(SAS)
∴PA=PB
结论:
线段垂直平分线上的点与这条线段两个端点的距离相等
线段平分线上的点与这条线段两个端点的距离相等。
线段垂直平分线的性质:
P
A
l
C
B
几何语言:
∵ l ⊥AB,AC=BC
∴PA=PB
探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线l上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线l上.
A
B
P
C
l
探索并证明线段垂直平分线的判定
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线l上.
A
B
P
C
l
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段垂直平分线的判定:
几何语言:
∵ PA=PB
∴ 点P在AB的垂直平分线l上
A
B
P
C
l
这些点能组成什么几何图形?
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.
A
B
P
C
l
1、∵ ,∴AB=AC。
理由:
2、∵ ,∴A在线段BC的中垂线上
理由:
AD是BC的中垂线
AB=AC
线段垂直平分线上的点与这条线段两个端点的距离相等.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
B
C
A
D
3、如图, NM是线段AB的中垂线,
下列说法正确的有: 。
①AB⊥MN,②AD=DB, ③MN⊥AB, ④MD=DN,⑤AB是MN的垂直平分线
A
B
M
N
D
①②③
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
D
C
B
E
A
解:
∵ED是线段AB的垂直平分线
∴
∵ C△BCD=BD+DC+BC
∴ C△BCD=
=
=
BD=AD
AD+DC+BC
AC+BC
12+7=19
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.
课堂练习
练习3 如图,AB =AC,MB =MC.直线AM 是线段
BC 的垂直平分线吗?
A
B
C
D
M
练习2:如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
练习3:如图,与图形A成轴对称的是哪个图形?画出它们的对称轴.
练习4:如图,在Rt△ABC中,∠C=90°,AD是角平分线且AD=BD,AC=10. 求AB的长度.
提示:过点D作DE⊥AB于E
A
B
C
D
E
(1)说一说本节课我们学习了哪些内容?你有什么收获?
课堂小结
1.垂直平分线的定义:
∵MN是AB的垂直平分线
∴ , ;
2.垂直平分线的性质:
∵MN是AB的垂直平分线
∴ ( )
3.垂直平分线的判定:
∵PA=PB
∴ (
)
MN⊥AB
P
A
B
M
N
D
AD=BD
PA=PB
线段垂直平分线上点与这条线段两个端点的距离相等
P在AB的垂直平分线上
与一条线段两个端点距
离相等的点,在这条线段的垂直平分线上
