13.2.2画轴对称图形第2课时(人教版)课件
文档属性
| 名称 | 13.2.2画轴对称图形第2课时(人教版)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 887.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-13 00:00:00 | ||
图片预览





文档简介
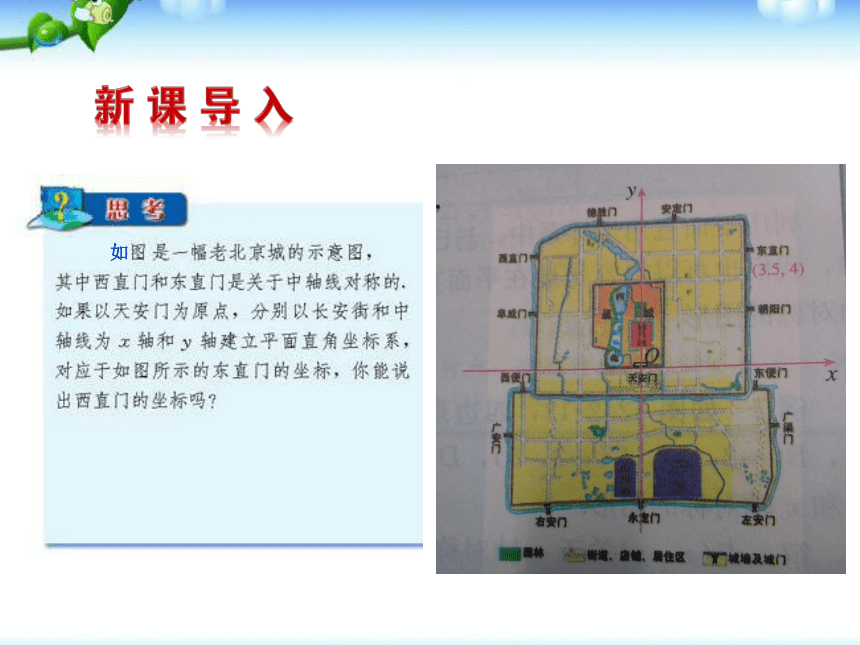
课件33张PPT。课前回顾1、如何建立平面直角坐标系?各个象限点的坐标的特征是什么?
2、如何在平面直角坐标系中描出点A(-2,3)?
3、你能画出上图中点A关于X轴对称的点吗?13.2 画轴对称图形
第2课时1.理解在平面直角坐标系中,已知点关于x 轴或y 轴对称的点的坐标的变化规律.
2.掌握在平面直角坐标系中作出一个图形的轴对称图形的方法..如自学指导1:看课本P69思考以下的部分,完成以下问题:
(1)在直角坐标系中画出下列已知点.
A(2,-3),B(-1,2),C(-6,-5),D( ,1),E(4, 0),F (0,-3)
(2)画出这些点分别关于x轴、y轴对称的点.并填写表格.
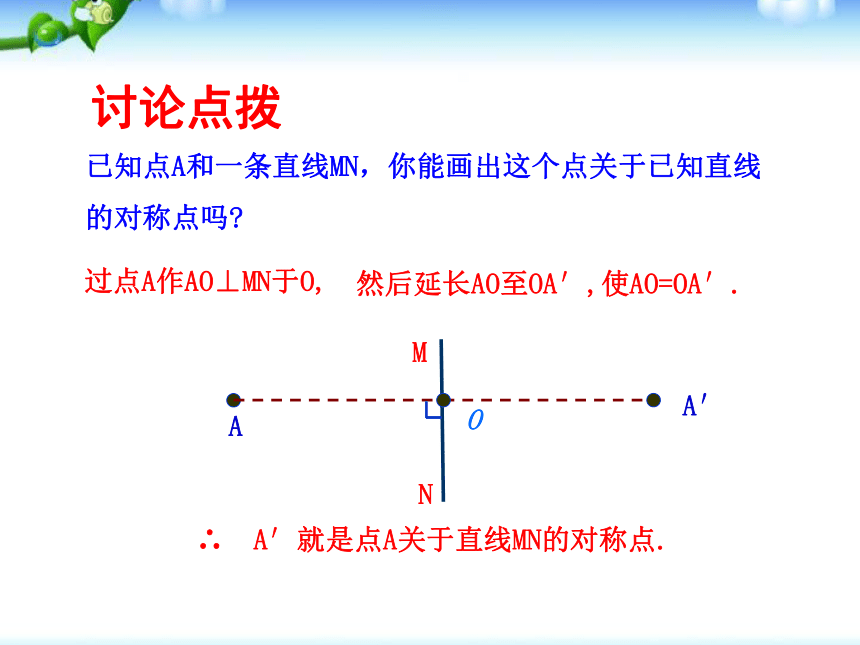
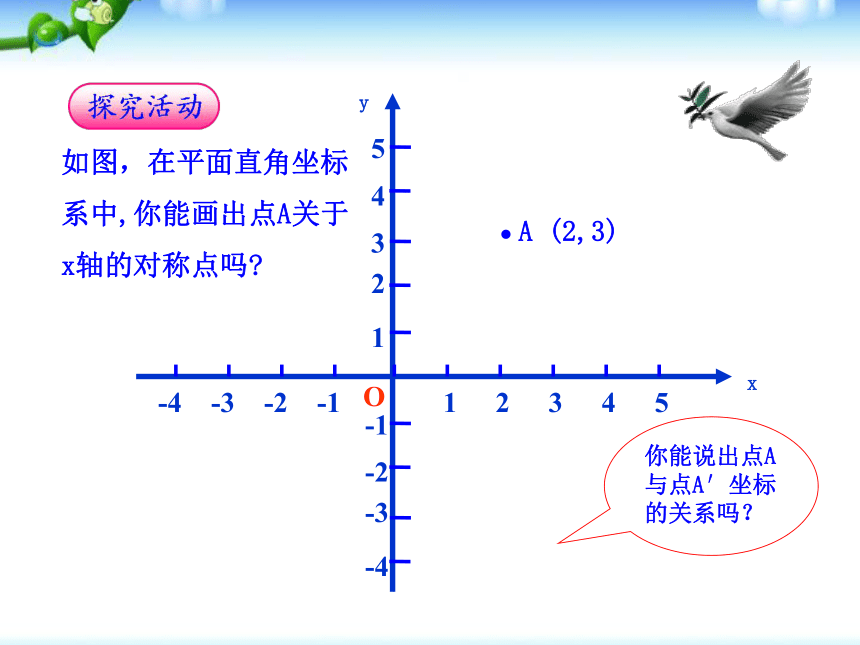
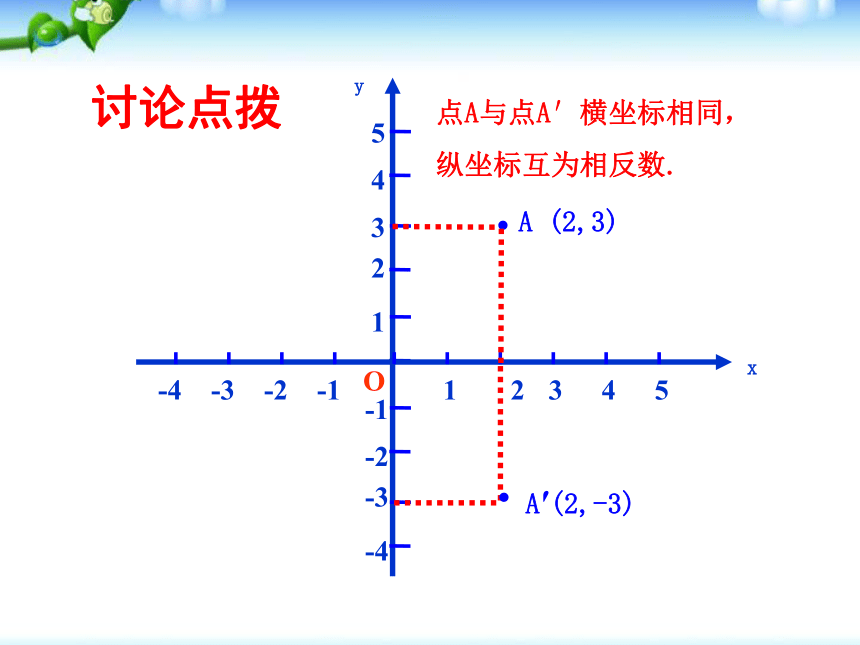
(3)请你仔细观察点的坐标,你能发现每对对称点的坐标有什么规律吗?已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗?AA′MN∴ A′就是点A关于直线MN的对称点.O然后延长AO至OA′,使AO=OA′.过点A作AO⊥MN于O,讨论点拨·OA (2,3)你能说出点A与点A′坐标的关系吗?如图,在平面直角坐标系中,你能画出点A关于x轴的对称点吗?yx·12345-4-3-2-1A (2,3)·A′(2,-3)点A与点A′横坐标相同,
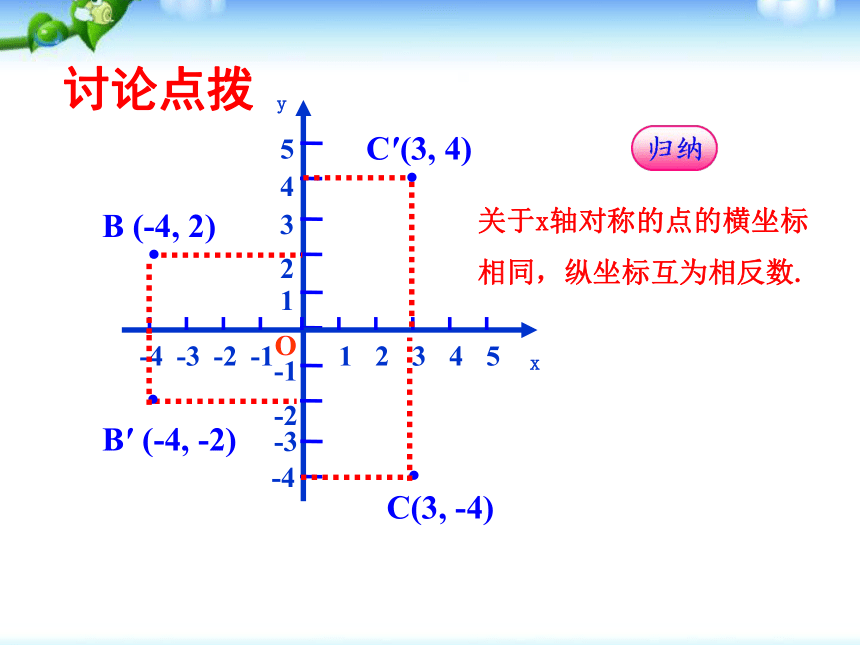
纵坐标互为相反数.xyO讨论点拨B (-4, 2)··C(3, -4)关于x轴对称的点的坐标具有怎样的关系?在平面直角坐标系中画出下列各点关于x轴的对称点.yxO讨论点拨31425-2-4-1-3B (-4, 2)··C(3, -4)·B′ (-4, -2)·C′(3, 4)关于x轴对称的点的横坐标
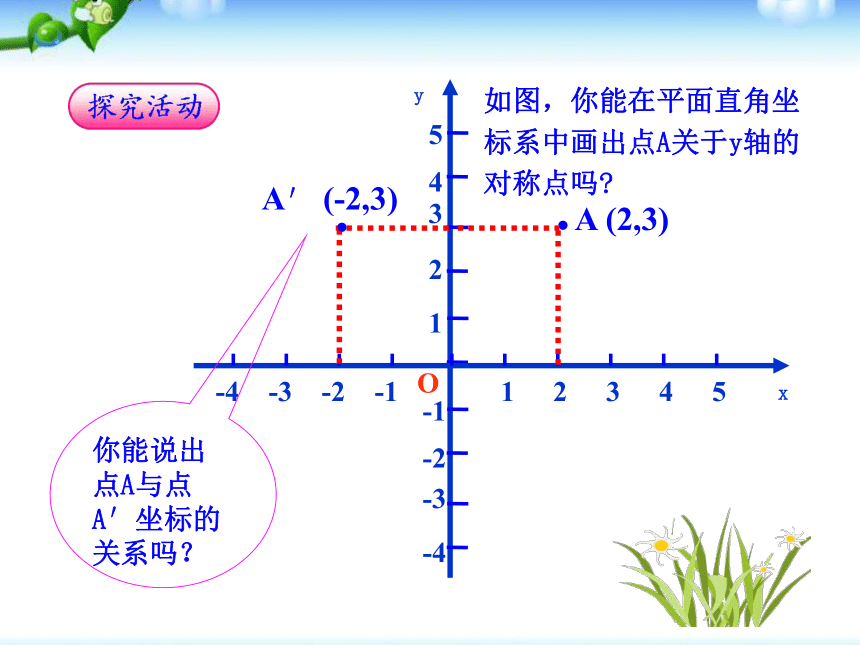
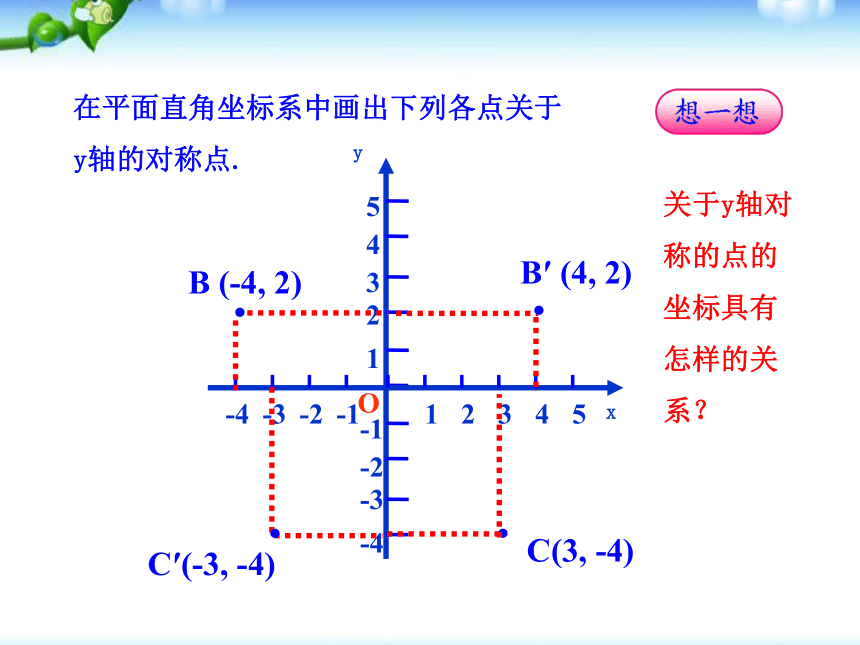
相同,纵坐标互为相反数.yxO讨论点拨·31425-2-4-1-3A (2,3)·A′ (-2,3)你能说出点A与点A′坐标的关系吗?如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗?yxOB (-4, 2)··C(3, -4)·B′ (4, 2)·C′(-3, -4)关于y轴对称的点的坐标具有怎样的关系?在平面直角坐标系中画出下列各点关于y轴的对称点.yxO 关于y轴对称的点的横坐标互为相反数, 纵坐标相等.点(x, y)关于x轴对称的点的坐标为________.
点(x, y)关于y轴对称的点的坐标为________.(x,-y)(-x,y)讨论点拨 练习1 分别写出下列各点关于x 轴和y 轴对称的点
的坐标:(-2,6),(1,-2),(-1,3),
(-4,-2),(1,0) . 解:关于x 轴对称的点的坐标:(-2, -6),
(1,2),(-1, -3),(-4,2),(1,0) .
关于y 轴对称的点的坐标:(2,6),
(-1,-2),(1,3),(4,-2),(-1,0) .课堂练习 练习2 若点P(2a+b,-3a)与点P′(8,b+2)
关于x 轴对称,则a = ,b= ;若关于y 轴对
称,则a = ,b=______.
课堂练习4-202 6自学指导2: 看课本P70例2,试着完成其中的填空和画图 例 如图,四边形ABCD 的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD 关
于x 轴和y 轴对称的图形.讨论点拨运用变化规律作图 解:点(x,y)关于y 轴对称的点的坐标为
(-x,y),因此四边形
ABCD 的顶点A,B,C,
D 关于y 轴对称的点分别
为:
A′( , ),
B′( , ),
C′( , ),
D′( , ),2 55 12 15 4运用变化规律作图解:依次连接 , , , ,
就可得到与四边形ABCD
关于y轴对称的四边形
.A′B′C′D′ A′B′ B′C′ C′D′ D′A′ 请在图上画出四边形ABCD 关于x 轴对称的图形. 运用变化规律作图 先求出已知图形中一些特殊点(多边形的顶点)的
对称点的坐标,描出并连接这些点,就可以得到这个图
形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线. 归纳画一个图形关于x 轴或y 轴对称的图形的方法
和步骤. 讨论点拨课堂练习 P课本71练习第2 ,3 课堂练习 课本P71习题13.2第三题
以正方形ABCD 的中心为原点建立平面直
角坐标系.点A 的坐标为(1,1)、写出点B,C,D
的坐标.1.点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____,b =_____.(- 5 ,-6 )-25【课堂练习】3.点P(-3, 2)与点Q关于y轴对称,则点Q的坐标为__________.
4.点M(a, -6)与点N(-2, b)关于y轴对称,则a=_____,
b =_____.( 3 , 2 )2-6【课堂练习】(1)本节课学习了哪些内容?
(2)在平面直角坐标系中,已知点关于x 轴或y 轴的
对称点的坐标有什么变化规律,如何判断两个
点是否关于x 轴或y 轴对称?
(3)说一说画一个图形关于x 轴或y 轴对称的图形的
方法和步骤. 1.关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等. 2.在平面直角坐标系中画一个图形关于x轴或y轴的对称图形:先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
通过本课时的学习,需要我们掌握:课外作业必做题:1、课本P72 习题13.2
第1、2题做在课本上
第5、6、7 做在课本上
第4题做在作业本上
补充题:在平面直角坐标系中先依次连接点A(-3,5),B(-2,-2),C(1,2),D(1,1),得到一个几何图形,再画出此图形关于y轴对称的图形,看看得到的图形像什么?
成功:A=x+y+z.A代表成功,x代表艰苦的劳动,y代表正确的方法,Z代表少说空话.
——爱因斯坦 1.完成下表:(-3,-3)(3, 3)(-1,-2)(1, 2)(8,-5)(-8,5)(0, -1)(0,1)(-4,0)(4,0)2.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a=_____,b=_______.
若点P与点P′关于y轴对称,则a=_____,b=_______.246-20【课堂练习补充】x=1·····P(-2,3)M(-1,1)N′ (5,-2)N(-3,-2)M′ (3,1)P′(4,3)3.如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗?·yx(1)在平面直角坐标系中,点(x,y)关于直线x=1对称点的坐标是多少? (2)在平面直角坐标系中,点(x,y)关于直线x=-1对称点的坐标是多少? (3)在平面直角坐标系中,点(x,y)关于直线y=1对称点的坐标是多少? (4)在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是多少?(-x+2,y)(-x-2,y)(x,-y+2)(x,-y-2)
2、如何在平面直角坐标系中描出点A(-2,3)?
3、你能画出上图中点A关于X轴对称的点吗?13.2 画轴对称图形
第2课时1.理解在平面直角坐标系中,已知点关于x 轴或y 轴对称的点的坐标的变化规律.
2.掌握在平面直角坐标系中作出一个图形的轴对称图形的方法..如自学指导1:看课本P69思考以下的部分,完成以下问题:
(1)在直角坐标系中画出下列已知点.
A(2,-3),B(-1,2),C(-6,-5),D( ,1),E(4, 0),F (0,-3)
(2)画出这些点分别关于x轴、y轴对称的点.并填写表格.
(3)请你仔细观察点的坐标,你能发现每对对称点的坐标有什么规律吗?已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗?AA′MN∴ A′就是点A关于直线MN的对称点.O然后延长AO至OA′,使AO=OA′.过点A作AO⊥MN于O,讨论点拨·OA (2,3)你能说出点A与点A′坐标的关系吗?如图,在平面直角坐标系中,你能画出点A关于x轴的对称点吗?yx·12345-4-3-2-1A (2,3)·A′(2,-3)点A与点A′横坐标相同,
纵坐标互为相反数.xyO讨论点拨B (-4, 2)··C(3, -4)关于x轴对称的点的坐标具有怎样的关系?在平面直角坐标系中画出下列各点关于x轴的对称点.yxO讨论点拨31425-2-4-1-3B (-4, 2)··C(3, -4)·B′ (-4, -2)·C′(3, 4)关于x轴对称的点的横坐标
相同,纵坐标互为相反数.yxO讨论点拨·31425-2-4-1-3A (2,3)·A′ (-2,3)你能说出点A与点A′坐标的关系吗?如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗?yxOB (-4, 2)··C(3, -4)·B′ (4, 2)·C′(-3, -4)关于y轴对称的点的坐标具有怎样的关系?在平面直角坐标系中画出下列各点关于y轴的对称点.yxO 关于y轴对称的点的横坐标互为相反数, 纵坐标相等.点(x, y)关于x轴对称的点的坐标为________.
点(x, y)关于y轴对称的点的坐标为________.(x,-y)(-x,y)讨论点拨 练习1 分别写出下列各点关于x 轴和y 轴对称的点
的坐标:(-2,6),(1,-2),(-1,3),
(-4,-2),(1,0) . 解:关于x 轴对称的点的坐标:(-2, -6),
(1,2),(-1, -3),(-4,2),(1,0) .
关于y 轴对称的点的坐标:(2,6),
(-1,-2),(1,3),(4,-2),(-1,0) .课堂练习 练习2 若点P(2a+b,-3a)与点P′(8,b+2)
关于x 轴对称,则a = ,b= ;若关于y 轴对
称,则a = ,b=______.
课堂练习4-202 6自学指导2: 看课本P70例2,试着完成其中的填空和画图 例 如图,四边形ABCD 的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD 关
于x 轴和y 轴对称的图形.讨论点拨运用变化规律作图 解:点(x,y)关于y 轴对称的点的坐标为
(-x,y),因此四边形
ABCD 的顶点A,B,C,
D 关于y 轴对称的点分别
为:
A′( , ),
B′( , ),
C′( , ),
D′( , ),2 55 12 15 4运用变化规律作图解:依次连接 , , , ,
就可得到与四边形ABCD
关于y轴对称的四边形
.A′B′C′D′ A′B′ B′C′ C′D′ D′A′ 请在图上画出四边形ABCD 关于x 轴对称的图形. 运用变化规律作图 先求出已知图形中一些特殊点(多边形的顶点)的
对称点的坐标,描出并连接这些点,就可以得到这个图
形的轴对称图形.
步骤简述为:
(1)求特殊点的坐标;(2)描点;(3)连线. 归纳画一个图形关于x 轴或y 轴对称的图形的方法
和步骤. 讨论点拨课堂练习 P课本71练习第2 ,3 课堂练习 课本P71习题13.2第三题
以正方形ABCD 的中心为原点建立平面直
角坐标系.点A 的坐标为(1,1)、写出点B,C,D
的坐标.1.点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____,b =_____.(- 5 ,-6 )-25【课堂练习】3.点P(-3, 2)与点Q关于y轴对称,则点Q的坐标为__________.
4.点M(a, -6)与点N(-2, b)关于y轴对称,则a=_____,
b =_____.( 3 , 2 )2-6【课堂练习】(1)本节课学习了哪些内容?
(2)在平面直角坐标系中,已知点关于x 轴或y 轴的
对称点的坐标有什么变化规律,如何判断两个
点是否关于x 轴或y 轴对称?
(3)说一说画一个图形关于x 轴或y 轴对称的图形的
方法和步骤. 1.关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等. 2.在平面直角坐标系中画一个图形关于x轴或y轴的对称图形:先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
通过本课时的学习,需要我们掌握:课外作业必做题:1、课本P72 习题13.2
第1、2题做在课本上
第5、6、7 做在课本上
第4题做在作业本上
补充题:在平面直角坐标系中先依次连接点A(-3,5),B(-2,-2),C(1,2),D(1,1),得到一个几何图形,再画出此图形关于y轴对称的图形,看看得到的图形像什么?
成功:A=x+y+z.A代表成功,x代表艰苦的劳动,y代表正确的方法,Z代表少说空话.
——爱因斯坦 1.完成下表:(-3,-3)(3, 3)(-1,-2)(1, 2)(8,-5)(-8,5)(0, -1)(0,1)(-4,0)(4,0)2.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a=_____,b=_______.
若点P与点P′关于y轴对称,则a=_____,b=_______.246-20【课堂练习补充】x=1·····P(-2,3)M(-1,1)N′ (5,-2)N(-3,-2)M′ (3,1)P′(4,3)3.如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗?·yx(1)在平面直角坐标系中,点(x,y)关于直线x=1对称点的坐标是多少? (2)在平面直角坐标系中,点(x,y)关于直线x=-1对称点的坐标是多少? (3)在平面直角坐标系中,点(x,y)关于直线y=1对称点的坐标是多少? (4)在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是多少?(-x+2,y)(-x-2,y)(x,-y+2)(x,-y-2)
