18.2函数的图象
图片预览


文档简介
课件16张PPT。2.函数的定义的理解:复习回顾:即任给一个________,一定能得到唯一一个________。进而可以得到一对_____________。1.平面直角坐标系的重要性质: 平面直角坐标系内的______与___________(即坐标)__________。(1)点——有序实数对,即坐标(m,n);
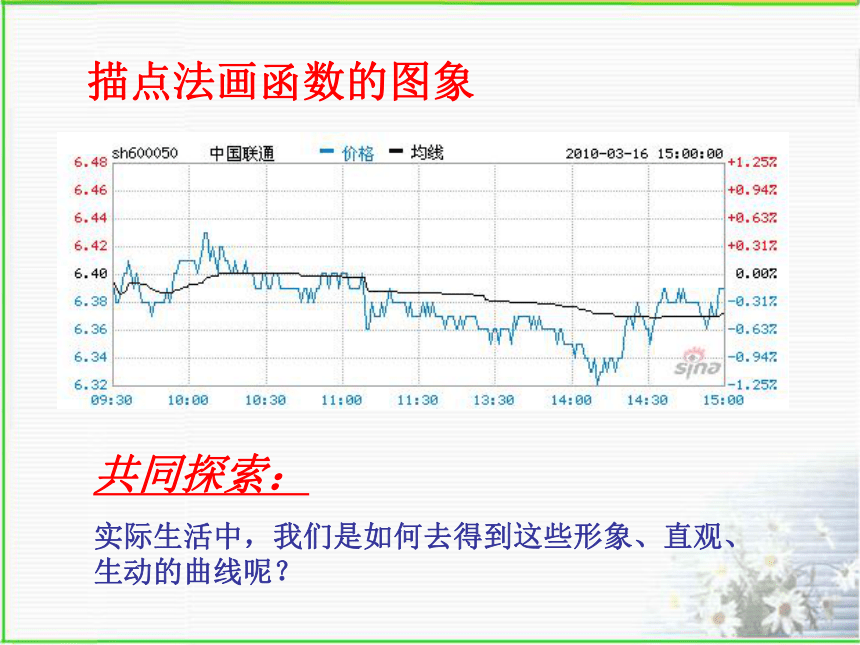
(2)有序实数对(m,n)——点(m,n)。3.函数的表示方法:(1)解析法;(2)列表法;(3)图象法。点有序实数对一一对应自变量x函数值y有序实数对(x,y)思考:阅读下面2010年5月18日中国联通和招商银行的股票K线图,你能获取什么信息?如果你是投资者,你会做出什么决定? 函数的图象可以表现出函数值随自变量的变化情况和规律,形象、直观、生动、通俗易懂。描点法画函数的图象共同探索:
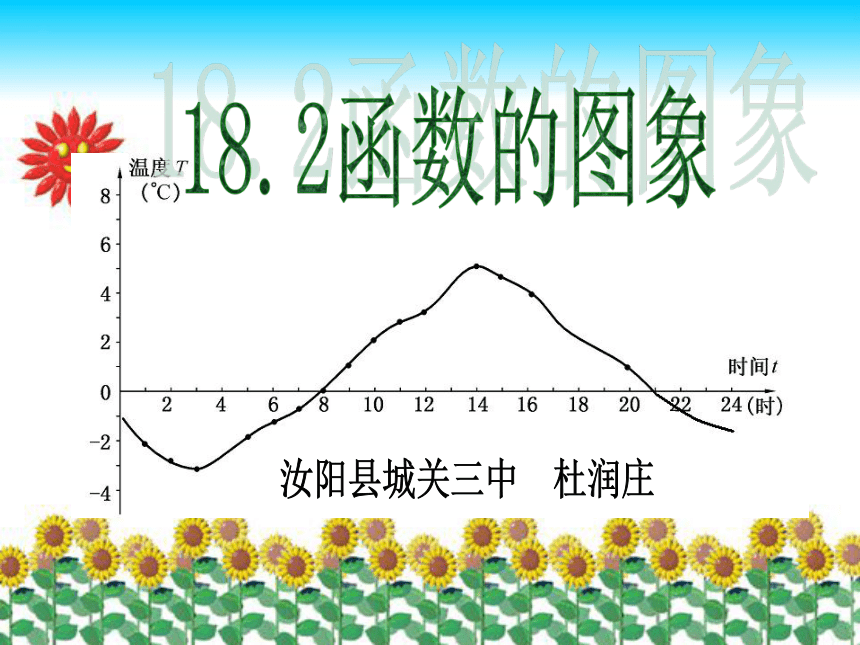
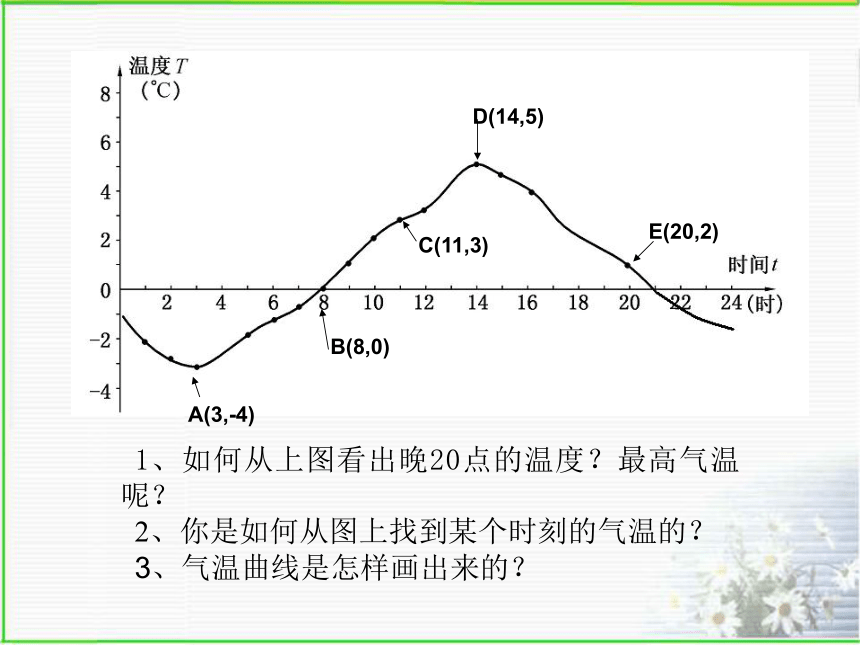
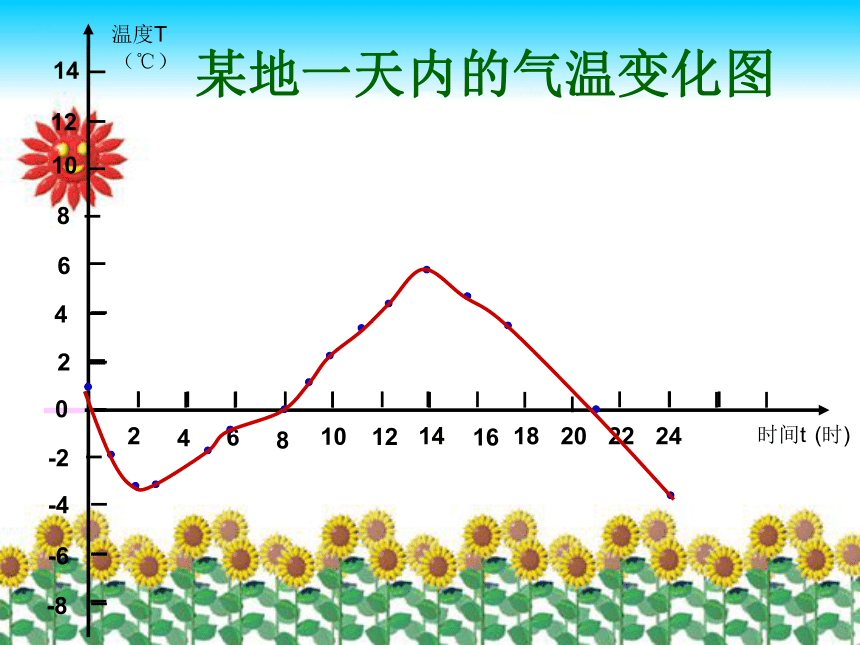
实际生活中,我们是如何去得到这些形象、直观、生动的曲线呢?18.2函数的图象汝阳县城关三中 杜润庄B(8,0)D(14,5)A(3,-4)C(11,3)E(20,2)161210864268 2-2-4-6-8温度T时间t(时)(℃)1418222024 04101214某地一天内的气温变化图共同探索:如何得到一个函数的图象?任给一个自变量x,一定能得到唯一一个函数值y。平面直角坐标系内的点与有序实数对(即坐标)一一对应。则:任意一对有序实数对(x,y)——点(x,y)。取一自变量x得一函数值y得一坐标(x,y)描得一点那么:我们就可以在平面直角坐标系中描出一点(x,y)。则:一定可以得到一对有序实数对(x,y)。思考:如果我们把所有能满足函数的点都描出来呢?在平面直角坐标系中,用函数自变量的某一个值x表示横坐标与它对应的函数值y表示纵坐标确定一个点(x,y)满足函数的一系列点组成的图形叫该函数的图象。重要结论:画出一个函数的图象的理论依据和思路:取一自变量x得一函数值y得一坐标(x,y)描得一点由这一系列的对应值,可以得到一系列的有序实数对:
…,(-3,4.5),(-2,2),(-1,0.5),(0,0),(1,0.5),(2,2),(3,4.5),…
例1:(1)列表由一系列的有序实数对,我们可以在平面直角坐标系中描画出一系列的点。(2)描点(3)连线通常,用光滑曲线依次把这些点连起来,便可得到这个函数的图象,如图所示 例1:(1)列表例2:画出下列函数的图象y=x+0.5①列表(自变量x可以取一切实数)②描点y=x+0.5③连线1、通常,用光滑曲线依次把这些点连起来,便可得到这个函数的图象.2、这里画函数图象的方法,可以概括为列表、描点、连线三步,通常称为描点法.注意3、我们画出的函数图象只是近似的大致图象。思考:如何才能让我们画出的函数图象更精确?答:取的点越多、越密集,图象越精确。练习:画出函数 y =的图象.解:●●●●●●●●在平面直角坐标系中,用函数自变量的某一个值x表示横坐标与它对应的函数值y表示纵坐标确定一个点(x,y)满足函数的一系列点组成的图形叫该函数的图象。知识总结:3.画出一个函数的图象的基本思路:取一自变量x得一函数值y得一坐标(x,y)描得一点1.函数的图象的优点:
函数的图象可以表现出函数值随自变量的变化情况和规律,形象、直观、生动、信息量丰富、通俗易懂。2.画函数的图象依据:由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.4.描点法画函数的图像:!注意:一般我们不可能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象.
描出的点越多,图象越精确.作业:2.画出函数 y =-2x+3的图象。
3.画出函数y=2x2-1的图象。
(2)有序实数对(m,n)——点(m,n)。3.函数的表示方法:(1)解析法;(2)列表法;(3)图象法。点有序实数对一一对应自变量x函数值y有序实数对(x,y)思考:阅读下面2010年5月18日中国联通和招商银行的股票K线图,你能获取什么信息?如果你是投资者,你会做出什么决定? 函数的图象可以表现出函数值随自变量的变化情况和规律,形象、直观、生动、通俗易懂。描点法画函数的图象共同探索:
实际生活中,我们是如何去得到这些形象、直观、生动的曲线呢?18.2函数的图象汝阳县城关三中 杜润庄B(8,0)D(14,5)A(3,-4)C(11,3)E(20,2)161210864268 2-2-4-6-8温度T时间t(时)(℃)1418222024 04101214某地一天内的气温变化图共同探索:如何得到一个函数的图象?任给一个自变量x,一定能得到唯一一个函数值y。平面直角坐标系内的点与有序实数对(即坐标)一一对应。则:任意一对有序实数对(x,y)——点(x,y)。取一自变量x得一函数值y得一坐标(x,y)描得一点那么:我们就可以在平面直角坐标系中描出一点(x,y)。则:一定可以得到一对有序实数对(x,y)。思考:如果我们把所有能满足函数的点都描出来呢?在平面直角坐标系中,用函数自变量的某一个值x表示横坐标与它对应的函数值y表示纵坐标确定一个点(x,y)满足函数的一系列点组成的图形叫该函数的图象。重要结论:画出一个函数的图象的理论依据和思路:取一自变量x得一函数值y得一坐标(x,y)描得一点由这一系列的对应值,可以得到一系列的有序实数对:
…,(-3,4.5),(-2,2),(-1,0.5),(0,0),(1,0.5),(2,2),(3,4.5),…
例1:(1)列表由一系列的有序实数对,我们可以在平面直角坐标系中描画出一系列的点。(2)描点(3)连线通常,用光滑曲线依次把这些点连起来,便可得到这个函数的图象,如图所示 例1:(1)列表例2:画出下列函数的图象y=x+0.5①列表(自变量x可以取一切实数)②描点y=x+0.5③连线1、通常,用光滑曲线依次把这些点连起来,便可得到这个函数的图象.2、这里画函数图象的方法,可以概括为列表、描点、连线三步,通常称为描点法.注意3、我们画出的函数图象只是近似的大致图象。思考:如何才能让我们画出的函数图象更精确?答:取的点越多、越密集,图象越精确。练习:画出函数 y =的图象.解:●●●●●●●●在平面直角坐标系中,用函数自变量的某一个值x表示横坐标与它对应的函数值y表示纵坐标确定一个点(x,y)满足函数的一系列点组成的图形叫该函数的图象。知识总结:3.画出一个函数的图象的基本思路:取一自变量x得一函数值y得一坐标(x,y)描得一点1.函数的图象的优点:
函数的图象可以表现出函数值随自变量的变化情况和规律,形象、直观、生动、信息量丰富、通俗易懂。2.画函数的图象依据:由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.4.描点法画函数的图像:!注意:一般我们不可能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象.
描出的点越多,图象越精确.作业:2.画出函数 y =-2x+3的图象。
3.画出函数y=2x2-1的图象。
