1.2全等三角形的判定（1）学案

三角形全等的判定（1）
__________________________________________________________________________________
1、理解全等三角形的判定方法SSS、SAS、ASA、AAS；
2、能运用判定方法判定两个三角形全等；
3、经理探索判定方法判定两个三角形全等的过程，体会数学知识来源生活，又应用于生活.
1．SSS
____________的两个三角形全等（简称SSS）．
这个定理说明，只要三角形的三边长度确定了，这个三角形的形状和大小就完全确定了，这也是三角形具有__________的原理．
2.利用SSS证明三角形全等
判断两个三角形全等的推理过程，叫做证明三角形全等．
如下图，已知：△ABC与△DEF的三条边对应相等，求证：△ABC≌△DEF．
( http: / / www.21cnjy.com / )
证明：在△ABC与△DEF中，
∴△ABC≌△DEF（SSS）．
3.利用SSS作一个角等于已知角
用直尺和圆规作一个角等于已知角的示意图如图所示，说明的依据是_________．
( http: / / www.21cnjy.com / )
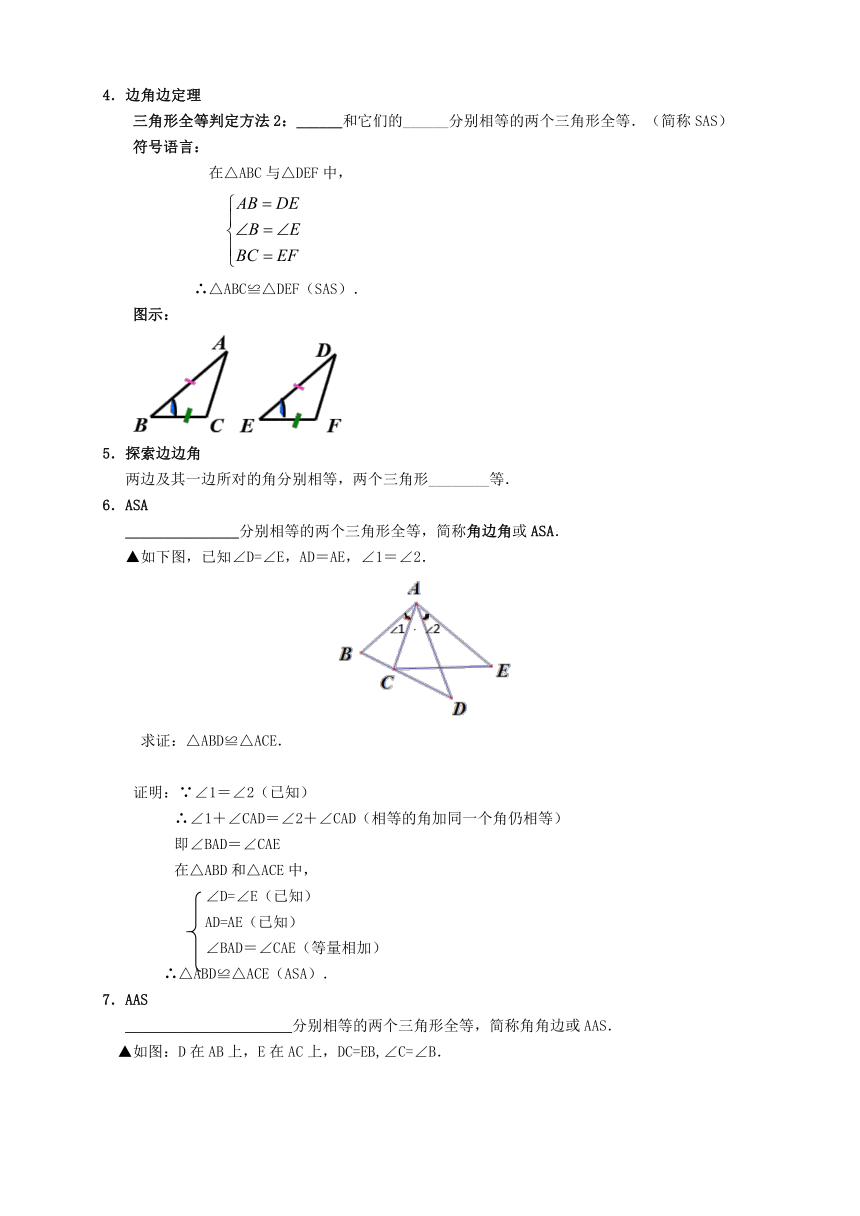
4．边角边定理
三角形全等判定方法2：______和它们的______分别相等的两个三角形全等．（简称SAS）
符号语言：
在△ABC与△DEF中，
∴△ABC≌△DEF（SAS）．
图示：
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
5．探索边边角
两边及其一边所对的角分别相等，两个三角形________等．
6．ASA
_______________分别相等的两个三角形全等，简称角边角或ASA．
▲如下图，已知∠D=∠E，AD＝AE，∠1＝∠2．
( http: / / www.21cnjy.com / )
求证：△ABD≌△ACE．
证明：∵∠1＝∠2（已知）
∴∠1＋∠CAD＝∠2＋∠CAD（相等的角加同一个角仍相等）
即∠BAD＝∠CAE
在△ABD和△ACE中，
∠D=∠E（已知）
AD=AE（已知）
∠BAD＝∠CAE（等量相加）
∴△ABD≌△ACE（ASA）．
7．AAS
______________________分别相等的两个三角形全等，简称角角边或AAS．
▲如图：D在AB上，E在AC上，DC=EB,∠C=∠B．
( http: / / www.21cnjy.com / )
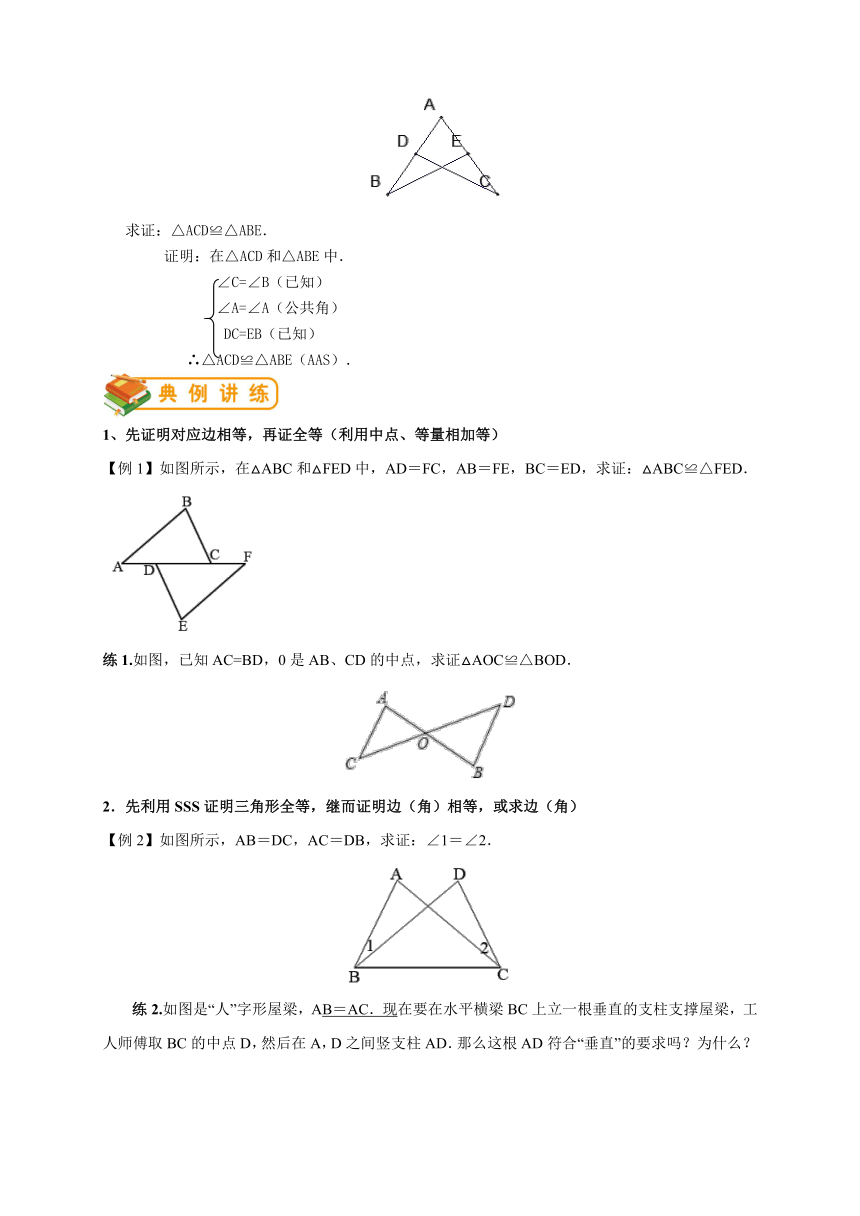
求证：△ACD≌△ABE．
证明：在△ACD和△ABE中．
∠C=∠B（已知）
∠A=∠A（公共角）
DC=EB（已知）
∴△ACD≌△ABE（AAS）．
1、先证明对应边相等，再证全等（利用中点、等量相加等）
【例1】如图所示，在△ABC和△FED中，AD＝FC，AB＝FE，BC＝ED，求证：△ABC≌△FED．
( http: / / www.21cnjy.com / )
练1.如图，已知AC=BD，0是AB、CD的中点，求证△AOC≌△BOD．
( http: / / www.21cnjy.com / )
2．先利用SSS证明三角形全等，继而证明边（角）相等，或求边（角）
【例2】如图所示，AB＝DC，AC＝DB，求证：∠1＝∠2．
( http: / / www.21cnjy.com / )
练2.如图是“人”字形屋梁，AB＝AC．现
( http: / / www.21cnjy.com )在要在水平横梁BC上立一根垂直的支柱支撑屋梁，工人师傅取BC的中点D，然后在A，D之间竖支柱AD．那么这根AD符合“垂直”的要求吗？为什么？
( http: / / www.21cnjy.com / )
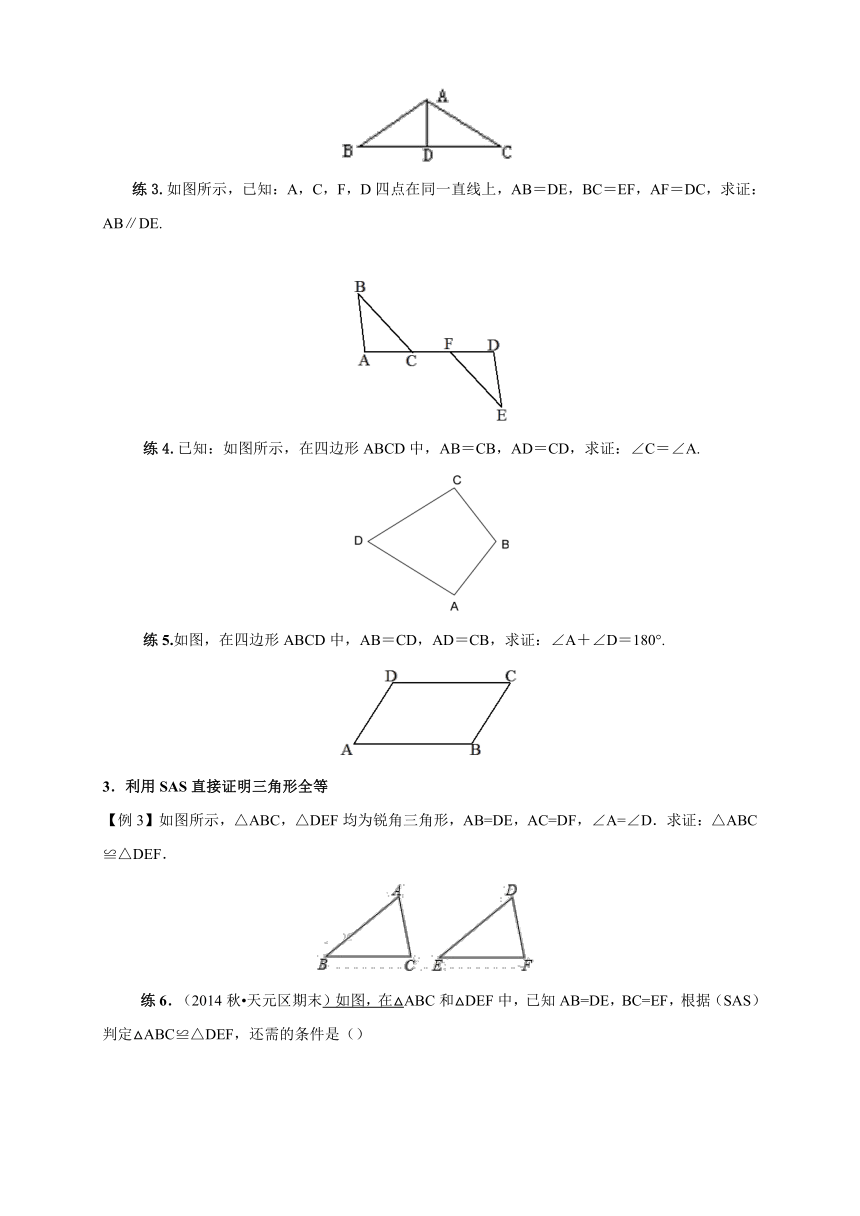
练3.如图所示，已知：A，C，F，D四点在同一直线上，AB＝DE，BC＝EF，AF＝DC，求证：AB∥DE.
( http: / / www.21cnjy.com / )
练4.已知：如图所示，在四边形ABCD中，AB＝CB，AD＝CD，求证：∠C＝∠A.
( http: / / www.21cnjy.com / )
练5.如图，在四边形ABCD中，AB＝CD，AD＝CB，求证：∠A＋∠D＝180°.
( http: / / www.21cnjy.com / )
3．利用SAS直接证明三角形全等
【例3】如图所示，△ABC，△DEF均为锐角三角形，AB=DE，AC=DF，∠A=∠D．求证：△ABC≌△DEF．
( http: / / www.21cnjy.com / )
练6．（2014秋 天元区期末）如图，在△
( http: / / www.21cnjy.com )ABC和△DEF中，已知AB=DE，BC=EF，根据（SAS）判定△ABC≌△DEF，还需的条件是（）
( http: / / www.21cnjy.com / )
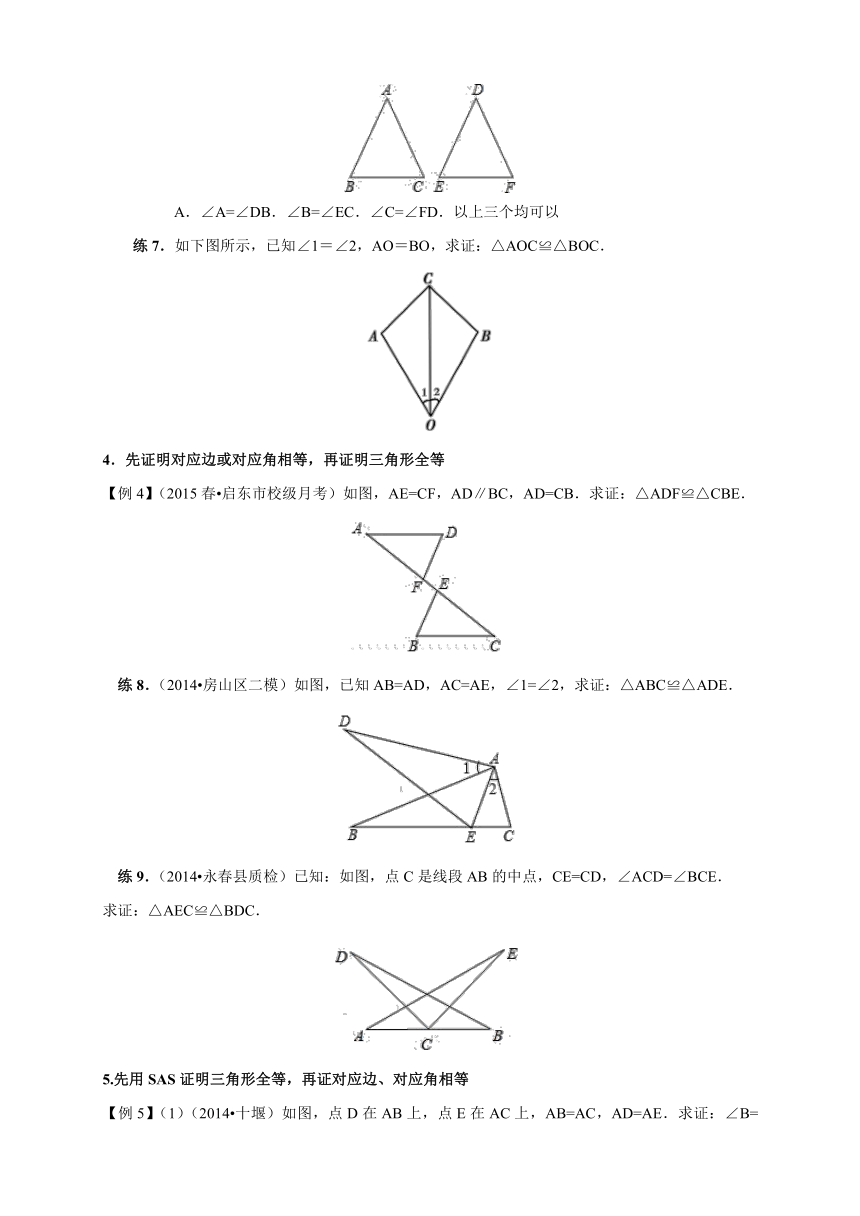
A．∠A=∠DB．∠B=∠EC．∠C=∠FD．以上三个均可以
练7．如下图所示，已知∠1＝∠2，AO＝BO，求证：△AOC≌△BOC．
( http: / / www.21cnjy.com / )
4．先证明对应边或对应角相等，再证明三角形全等
【例4】（2015春 启东市校级月考）如图，AE=CF，AD∥BC，AD=CB．求证：△ADF≌△CBE．
( http: / / www.21cnjy.com / )
练8．（2014 房山区二模）如图，已知AB=AD，AC=AE，∠1=∠2，求证：△ABC≌△ADE．
( http: / / www.21cnjy.com / )
练9．（2014 永春县质检）已知：如图，点C是线段AB的中点，CE=CD，∠ACD=∠BCE．
求证：△AEC≌△BDC．
( http: / / www.21cnjy.com / )
5.先用SAS证明三角形全等，再证对应边、对应角相等
【例5】（1）（2014 十堰）如图，点D在AB上，点E在AC上，AB=AC，AD=AE．求证：∠B=∠C．
( http: / / www.21cnjy.com / )
（2）（2015春 鼓楼区校级月考）如图，点E，F在AC上，AB∥CD，AB=CD，AE=CF．求证：BF=DE．
( http: / / www.21cnjy.com / )
练10．（2014秋 涞水县期末）如图，AB与CD交于点O，OA=OC，OD=OB，∠A=50°，∠B=30°，则∠D的度数为（）
( http: / / www.21cnjy.com / )
A．50°
B.30°C．80°D．100°
练11．（2014春 锦州
( http: / / www.21cnjy.com )校级期中）如图，点B，E，C，F在同一直线上，在△ABC与△DEF中，AB=DE，AC=DF，若∠_____=∠______，则△ABC≌△DEF，所以BC=_____，因此BE=________．
( http: / / www.21cnjy.com / )
6．先用ASA证全等，再证边角相等
【例6】如图所示，四边形ABCD的对角线AC与BD相交于O点，∠1＝∠2，∠3＝∠4．求证：BO＝DO．
练12.如图所示，在△ABC中，点O为AB的中点，AD∥BC，过点O的直线分别交AD，BC于点D，E，求证：OD＝OE.
7．先用AAS证全等，再证边角相等
【例7】如图所示，∠1＝∠2，∠C＝∠D，求证：AC＝AD．
练13.如图所示，C，F在BE上，∠A＝∠D，AC∥DF，BF＝EC．求证：AB＝DE．
8．灵活选用证明方法证（判断）全等
【例8】如图所示，已知∠B＝∠DEF，
( http: / / www.21cnjy.com )BC＝EF，要证△ABC≌△DEF，若要以“ASA”为依据，还缺条件_________；以“SAS”为依据，还缺条件_________；以“AAS”为依据，还缺条件_________.
练14.如图所示，点D在AB上，点E在AC上，且∠B＝∠C，那么补充下列一个条件后，仍无法判定△ABE≌△ACD的是（
）.
A.AD＝AE
B.∠AEB＝∠ADCC.BE＝CD
D.AB＝AC
练15.如图所示，BF⊥AC，DE⊥AC，垂足分别为点F，E，BF＝DE，∠B＝∠D，求证：AE＝CF.
练16．如图，将△BOD绕点O旋转
( http: / / www.21cnjy.com )180°后得到△AOC，再过点O任意画一条与AC，BD都相交的直线MN，交点分别为M和N．试问：线段OM＝ON成立吗？若成立，请进行证明；若不成立，请说明理由．
( http: / / www.21cnjy.com / )
练17．如图所示，直角三角形ABC的直角顶点C置于直线上，AC＝BC，现过A，B两点分别作直线的垂线，垂足分别为点D，E.
1．如图所示，AB∥CD，OB＝OD，则由“ASA”可以直接判定△______≌△___________.
2．如图所示，在△ABC中，AD⊥
( http: / / www.21cnjy.com )BC，CE⊥AB，垂足分别为点D，E，AD，CE交于点H，已知EH＝EB＝3，AE＝4，则CH的长是___________．
( http: / / www.21cnjy.com / )
3．如图所示，已知点E，C在线段BF上，BE＝CF，AB∥DE，∠ACB＝∠F．求证：△ABC≌△DEF．
4．如图所示，已知∠B＝∠E，∠BAD＝∠EAC，AC＝AD，求证：AB＝AE.
5.（2014 厦门校级一模）如图，A、B、C、D四点在同一条直线上，AB=CD，EC=DF，EC∥DF．求证：△ACE≌BDF．
( http: / / www.21cnjy.com / )
_________________________________________________________________________________
_________________________________________________________________________________
1.已知：如图，AB=CD，BE=DF，AF=EC。求证：BF=DE
( http: / / www.21cnjy.com / )
2.已知：如图AB=AC，AD=AE，BE和CD相交于G。求证：AG平分∠BAC
( http: / / www.21cnjy.com / )
3．如图，AB=CD，AD=BC，O是BD上任意一点，边O点的直线分别交AD，BC于M，N点，求证：∠1=∠2。
( http: / / www.21cnjy.com / )
4．如图，已知AC//FD，AF//CD，FB//EC。求证：△AFB≌△DCE。
( http: / / www.21cnjy.com / )
5．如图，已知AD//BC，∠DAB和∠ABC的平分线相交于E，过E的直线交AD于D，交BC于C。求证：DE=EC。
( http: / / www.21cnjy.com / )
6．已知：如图，在△ABC中，延长AC边中线BE到G，使EG=BE，延长AB边中线CD到F，使DF=CD。求证：G，A，F在同一直线上。
( http: / / www.21cnjy.com / )
7．已知：如图，在△ABC中，∠B=60°，△ABC的角平分线AD，CE相交于点O。求证：AE+CD=AC。
( http: / / www.21cnjy.com / )
8．如图，EA平分∠CAB，且AB=AC+BD，E为CD中点，求证：BE平分∠ABD。
( http: / / www.21cnjy.com / )
9．（2014年理工附期
( http: / / www.21cnjy.com )中）已知：如图，D是△ABC中BC边上一点，E是AD上一点，EB=EC，∠ABE=∠ACE。求证：∠BAE=∠CAE。
( http: / / www.21cnjy.com / )
证明　在△AEB和△AEC中，
∴△AEB≌△ACE。（第一步）
∴∠BAE=∠CAE。（第二步）
问上面证明过程是否正确？若正确，请写出每一步推理的根据；若不正确，请指出错在哪一步，并写出正确过程。
D
C
B
A
O
1
2
3
4
A
D
B
E
C
O
A
B
C
F
E
D
A
D
B
E
F
C
B
A
C
D
E
D
C
E
F
A
B
A
C
D
F
E
B
A
D
C
B
O
C
E
B
F
D
A
A
B
C
D
E