3.7.1正多边形和圆 课件

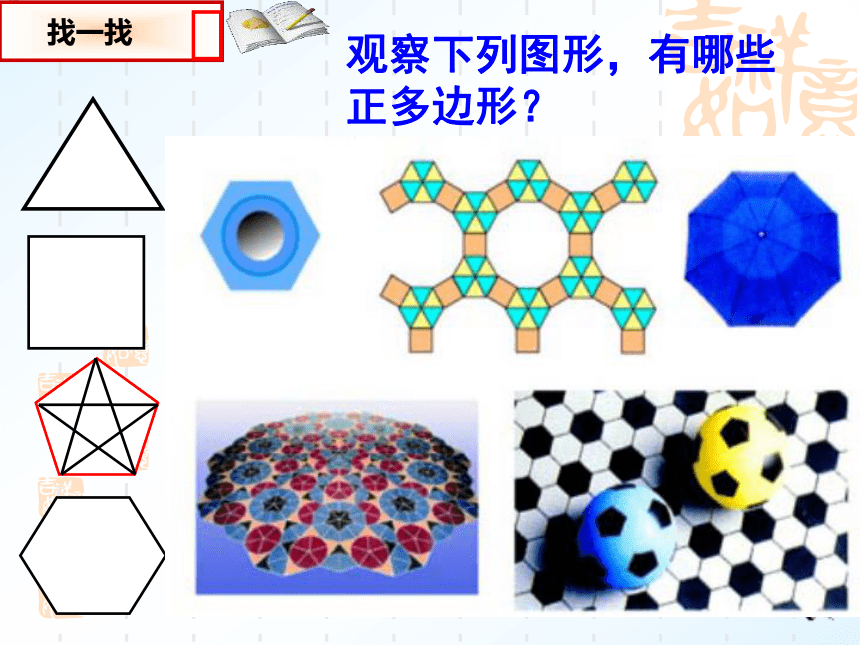
课件14张PPT。青岛版九年级上册3.7 正多边形和圆 观察下列图形，有哪些正多边形？各边相等,各角也相等的多边形是正多边形.
正n 边形：如果一个正多边形有n 条边，
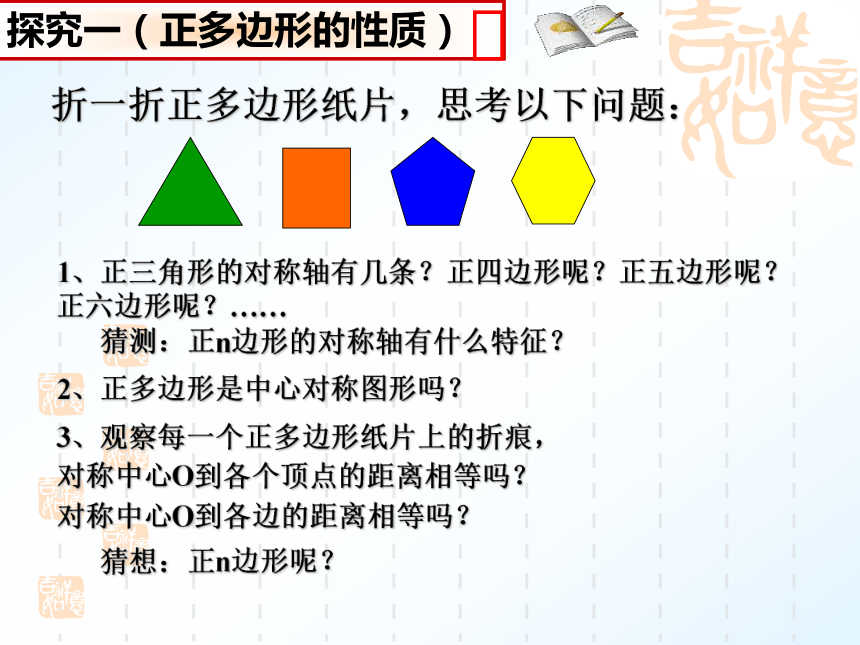
那么这个正多边形叫做正n 边形.正多边形定义 正n边形有 条边， 个角，内角和为 ，每个内角为 .n n (n -2)·180°折一折正多边形纸片，思考以下问题：1、正三角形的对称轴有几条？正四边形呢？正五边形呢？正六边形呢？……
猜测：正n边形的对称轴有什么特征？
2、正多边形是中心对称图形吗？

3、观察每一个正多边形纸片上的折痕，
对称中心O到各个顶点的距离相等吗？
对称中心O到各边的距离相等吗？
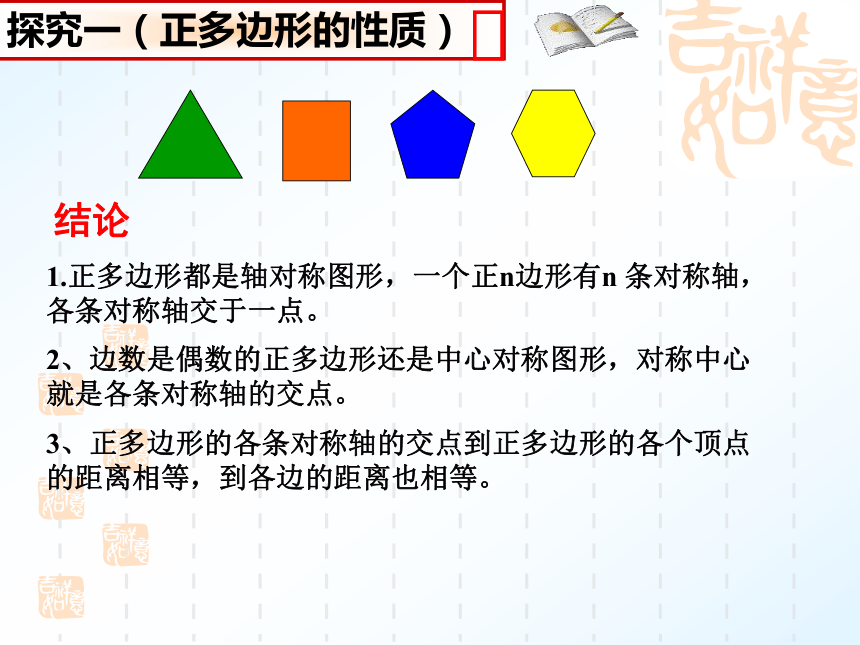
猜想：正n边形呢？ 1.正多边形都是轴对称图形，一个正n边形有n 条对称轴，
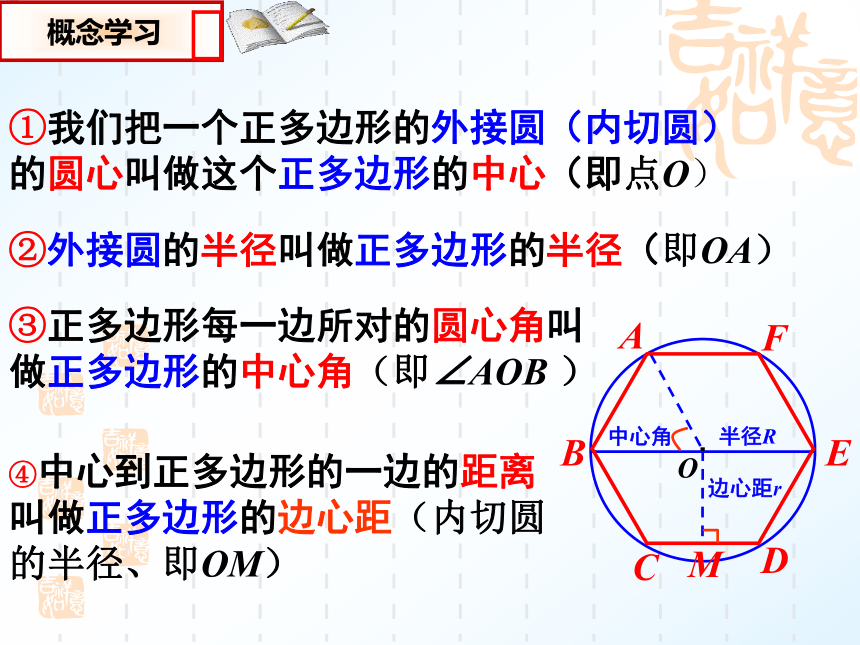
各条对称轴交于一点。2、边数是偶数的正多边形还是中心对称图形，对称中心就是各条对称轴的交点。3、正多边形的各条对称轴的交点到正多边形的各个顶点的距离相等，到各边的距离也相等。结论③正多边形每一边所对的圆心角叫做正多边形的中心角（即∠AOB ）①我们把一个正多边形的外接圆（内切圆）的圆心叫做这个正多边形的中心（即点O）②外接圆的半径叫做正多边形的半径（即OA）④中心到正多边形的一边的距离叫做正多边形的边心距（内切圆的半径、即OM）1.课本P112第2题M连接OC，由垂径定理（运用圆的有关知识）得.O中心角ABG边心距OG把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra例. 有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ，△OBC是等边三角形，从而正六边形的边长等于它的半径.因此,亭子地基的周长l =4×6=24(m).OABCDEFRPr利用勾股定理,可得边心距亭子地基的面积在Rt△OPC中,OC=4, PC=OABCDEFRPr1．（2013贵州毕节）正八边形的一个中心角的度数是（ ）度.45°2．（2013山东滨州）若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为（ ）
A、6， B、 ，3 C、6，3 D、 ，B 3．（2012咸宁中考）如图，⊙O的外切正六边形ABCDEF的边长为2，则图中阴影部分的面积为
（ ）
A、 B、 C、 D、
A 1.正多边和圆的有关概念：
正多边形的中心，正多边形的半径，
正多边形的中心角，正多边形的边心距．2.正多边形的半径、中心角、边长、
正多边的边心距之间的等量关系． 3.运用所学知识解决实际问题．