第23章解直角三角形单元测试题(1)(含答案)
文档属性
| 名称 | 第23章解直角三角形单元测试题(1)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 140.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-14 00:00:00 | ||
图片预览


文档简介
第23章
解直角三角形单元测试题(1)
(满分120分,120分钟完卷)
一、选择题:(30分)
1、已知α为锐角,则m=sinα+cosα的值(
)
A.m>1
B.m=1
C.m<1
D.m≥1
2、在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值
( )
A
也扩大3倍
B
缩小为原来的
C
都不变
D
有的扩大,有的缩小
3、以直角坐标系的原点O为圆心,以1为半径作圆。若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为
(
)
A
(cosα,1)
B
(1,sinα)
C
(sinα,cosα)
D
(cosα,sinα)
4、如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是
(
A
)
A、4cm
B、6cm
C、8cm
D、10cm
5、已知a为锐角,sina=cos500则a等于
(
)
A
20°
B
30°
C
40°
D
50°
6、若tan(a+10°)=,则锐角a的度数是
(
)
A、20°
B、30°
C、35°
D、50°
7、如果α、β都是锐角,下面式子中正确的是
(
)
A、sin(α+β)=sinα+sinβ
B、cos(α+β)=时,α+β=60°
C、若α≥β时,则cosα≥cosβ
D、若cosα>sinβ,则α+β>90°
8、小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30 角,且此时测得1米杆的影长为2米,则电线杆的高度为(
)
A.9米
B.28米
C.米
D.米
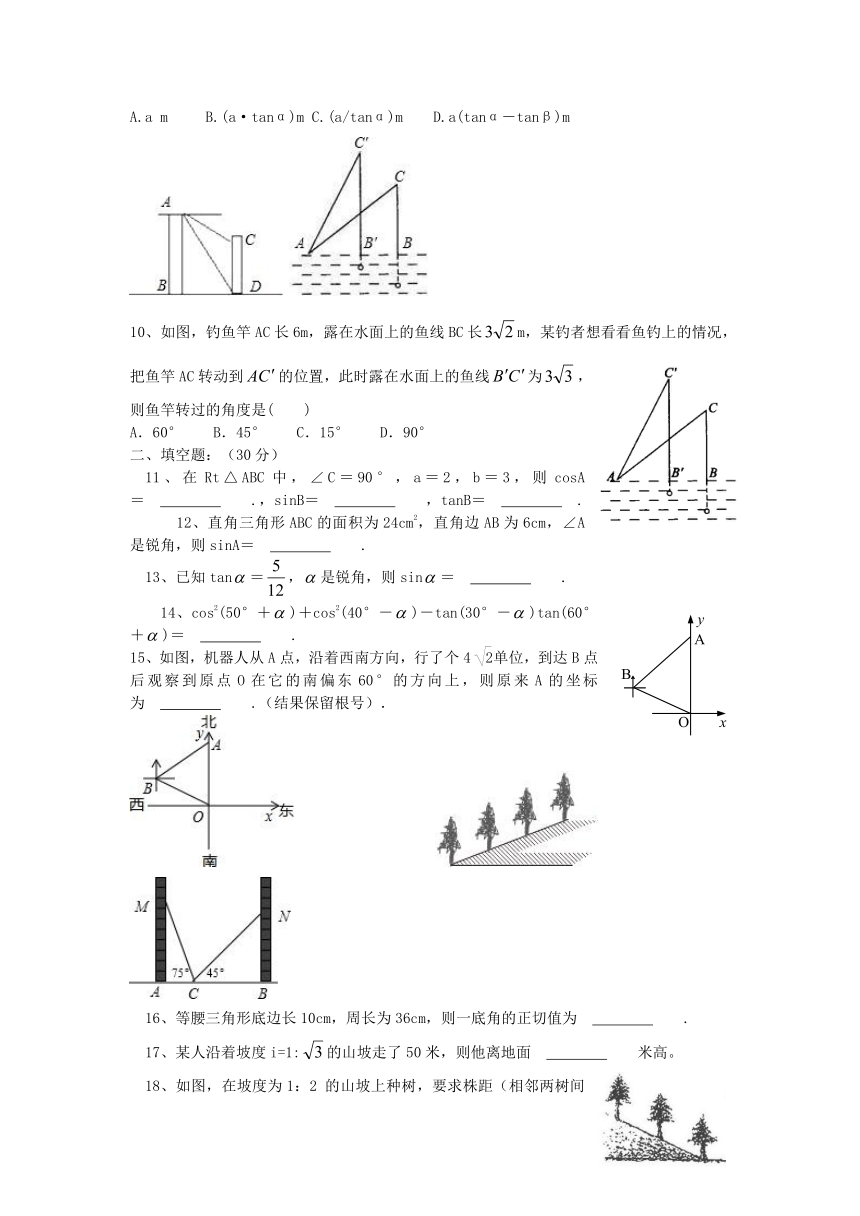
9、如图,两建筑物的水平距离为am,从A点测得D点的俯角为a,测得C点的俯角为β,则较低建筑物CD的高为
(
)
A.a
m
B.(a·tanα)m
C.(a/tanα)m
D.a(tanα-tanβ)m
10、如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是(
)
A.60°
B.45°
C.15°
D.90°
二、填空题:(30分)
11、在Rt△ABC中,∠C=90°,a=2,b=3,则cosA=
.,sinB=
,tanB=
.
12、直角三角形ABC的面积为24cm2,直角边AB为6cm,∠A是锐角,则sinA=
.
13、已知tan=,是锐角,则sin=
.
14、cos2(50°+)+cos2(40°-)-tan(30°-)tan(60°+)=
.
15、如图,机器人从A点,沿着西南方向,行了个4单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为
.(结果保留根号).
16、等腰三角形底边长10cm,周长为36cm,则一底角的正切值为
.
17、某人沿着坡度i=1:的山坡走了50米,则他离地面
米高。
18、如图,在坡度为1:2
的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是
米。
19、在△ABC中,∠ACB=90°,cosA=,AB=8cm
,则△ABC的面积为
.
20、如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时,梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面墙上N,此时梯子顶端距地面的垂直距离NB为b米,梯子的倾斜角45°,则这间房子的宽AB是
米。
三、解答题:(60分)
21、计算(8分):(1)tan30°sin60°+cos230°-sin245°tan45°
(2).
22、(6分)△ABC中,∠C=90°(1)已知:c=
8,∠A=60°,求∠B、a、b.
(2)
已知:a=3,
∠A=30°,求∠B、b、c.
23、(6分)
某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60 km/h(即m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)请在图中画出表示北偏东45°方向的射线AC,并标出点C的位置;
(2)点B坐标为
,点C坐标为
;
(3)一辆汽车从点B行驶到点C所用的时间为15 s,请通过计算,判断该汽车在限速公路上是否超速行驶?(本小问中)
24、
(6分)
已知Rt△ABC的斜边AB的长为10cm
,
sinA、sinB是方程m(x2-2x)+5(x2+x)+12=0的两根。求m的值。
25、(8分)如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连结CE,求sin∠ACE的值.
26、(8分)如图,某超市(大型商场)在一楼至二楼之间安装有电梯,天花板(一楼的楼顶墙壁)与地面平行,请你根据图中数据计算回答:小敏身高1.85米,他乘电梯会有碰头危险吗?(sin28o≈0.47,tan28o≈0.53)
27、(8分)如图,已知MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区。取MN上另一点B,测得BA的方向为南偏东75°.已知MB=400m,通过计算回答,如果不改变方向,输水线路是否会穿过居民区?
28、(10分)如图,点A(tanα,0),B(tanβ,0)在x轴的正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角;
(1)若二次函数y=-x2-kx+(2+2k-k2)的图象经过A、B两点,求它的解析式。
(2)点C在(1)中求出的二次函数的图象上吗 请说明理由。
参考答案
一、1、A
2、C
3、D
4、A
5、C
6、D
7、B
8、D
9、D
10、C
二、11、,,
12、
13、
14、0
15、(0,4+)
16、
17、25
18、3
19、
20、a
21(1)
(2)2
22、(1)∠B=30°,a=12,b=4(2)∠B=30°,b=9,c=6
23、解:(1)如图6所示,射线为AC,点C为所求位置.
(2)(,0);(100 ,0);
(3).
270÷15=18(m/s).∵,
∴这辆车在限速公路上超速行驶了.
24、m=20(m=-2舍)
25、
26、答案:作交于,则,
在中,(米).
所以,小敏不会有碰头危险.
27、不会穿过居民区。
过A作AH⊥MN于H,则∠ABH=45°,AH=BH
设AH=x,则BH=x,MH=x=x+400,∴x=200+200=546.1>500∴不会穿过居民区。
28、tanα·tanβ=k2―2k―2=1
∴k1=3(舍),k2=-1
∴解析式为y=―x2+x―1
(2)不在。
x
O
A
y
B
y/m
x/m
A(0,
-100)
B
O
60°
东
北
C
y/m
A(0,-100)
B
O
60°
图
6
x/m
45°
解直角三角形单元测试题(1)
(满分120分,120分钟完卷)
一、选择题:(30分)
1、已知α为锐角,则m=sinα+cosα的值(
)
A.m>1
B.m=1
C.m<1
D.m≥1
2、在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值
( )
A
也扩大3倍
B
缩小为原来的
C
都不变
D
有的扩大,有的缩小
3、以直角坐标系的原点O为圆心,以1为半径作圆。若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为
(
)
A
(cosα,1)
B
(1,sinα)
C
(sinα,cosα)
D
(cosα,sinα)
4、如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是
(
A
)
A、4cm
B、6cm
C、8cm
D、10cm
5、已知a为锐角,sina=cos500则a等于
(
)
A
20°
B
30°
C
40°
D
50°
6、若tan(a+10°)=,则锐角a的度数是
(
)
A、20°
B、30°
C、35°
D、50°
7、如果α、β都是锐角,下面式子中正确的是
(
)
A、sin(α+β)=sinα+sinβ
B、cos(α+β)=时,α+β=60°
C、若α≥β时,则cosα≥cosβ
D、若cosα>sinβ,则α+β>90°
8、小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30 角,且此时测得1米杆的影长为2米,则电线杆的高度为(
)
A.9米
B.28米
C.米
D.米
9、如图,两建筑物的水平距离为am,从A点测得D点的俯角为a,测得C点的俯角为β,则较低建筑物CD的高为
(
)
A.a
m
B.(a·tanα)m
C.(a/tanα)m
D.a(tanα-tanβ)m
10、如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是(
)
A.60°
B.45°
C.15°
D.90°
二、填空题:(30分)
11、在Rt△ABC中,∠C=90°,a=2,b=3,则cosA=
.,sinB=
,tanB=
.
12、直角三角形ABC的面积为24cm2,直角边AB为6cm,∠A是锐角,则sinA=
.
13、已知tan=,是锐角,则sin=
.
14、cos2(50°+)+cos2(40°-)-tan(30°-)tan(60°+)=
.
15、如图,机器人从A点,沿着西南方向,行了个4单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A的坐标为
.(结果保留根号).
16、等腰三角形底边长10cm,周长为36cm,则一底角的正切值为
.
17、某人沿着坡度i=1:的山坡走了50米,则他离地面
米高。
18、如图,在坡度为1:2
的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是
米。
19、在△ABC中,∠ACB=90°,cosA=,AB=8cm
,则△ABC的面积为
.
20、如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时,梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面墙上N,此时梯子顶端距地面的垂直距离NB为b米,梯子的倾斜角45°,则这间房子的宽AB是
米。
三、解答题:(60分)
21、计算(8分):(1)tan30°sin60°+cos230°-sin245°tan45°
(2).
22、(6分)△ABC中,∠C=90°(1)已知:c=
8,∠A=60°,求∠B、a、b.
(2)
已知:a=3,
∠A=30°,求∠B、b、c.
23、(6分)
某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60 km/h(即m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)请在图中画出表示北偏东45°方向的射线AC,并标出点C的位置;
(2)点B坐标为
,点C坐标为
;
(3)一辆汽车从点B行驶到点C所用的时间为15 s,请通过计算,判断该汽车在限速公路上是否超速行驶?(本小问中)
24、
(6分)
已知Rt△ABC的斜边AB的长为10cm
,
sinA、sinB是方程m(x2-2x)+5(x2+x)+12=0的两根。求m的值。
25、(8分)如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连结CE,求sin∠ACE的值.
26、(8分)如图,某超市(大型商场)在一楼至二楼之间安装有电梯,天花板(一楼的楼顶墙壁)与地面平行,请你根据图中数据计算回答:小敏身高1.85米,他乘电梯会有碰头危险吗?(sin28o≈0.47,tan28o≈0.53)
27、(8分)如图,已知MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区。取MN上另一点B,测得BA的方向为南偏东75°.已知MB=400m,通过计算回答,如果不改变方向,输水线路是否会穿过居民区?
28、(10分)如图,点A(tanα,0),B(tanβ,0)在x轴的正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角;
(1)若二次函数y=-x2-kx+(2+2k-k2)的图象经过A、B两点,求它的解析式。
(2)点C在(1)中求出的二次函数的图象上吗 请说明理由。
参考答案
一、1、A
2、C
3、D
4、A
5、C
6、D
7、B
8、D
9、D
10、C
二、11、,,
12、
13、
14、0
15、(0,4+)
16、
17、25
18、3
19、
20、a
21(1)
(2)2
22、(1)∠B=30°,a=12,b=4(2)∠B=30°,b=9,c=6
23、解:(1)如图6所示,射线为AC,点C为所求位置.
(2)(,0);(100 ,0);
(3).
270÷15=18(m/s).∵,
∴这辆车在限速公路上超速行驶了.
24、m=20(m=-2舍)
25、
26、答案:作交于,则,
在中,(米).
所以,小敏不会有碰头危险.
27、不会穿过居民区。
过A作AH⊥MN于H,则∠ABH=45°,AH=BH
设AH=x,则BH=x,MH=x=x+400,∴x=200+200=546.1>500∴不会穿过居民区。
28、tanα·tanβ=k2―2k―2=1
∴k1=3(舍),k2=-1
∴解析式为y=―x2+x―1
(2)不在。
x
O
A
y
B
y/m
x/m
A(0,
-100)
B
O
60°
东
北
C
y/m
A(0,-100)
B
O
60°
图
6
x/m
45°
