人教版选修2-2导数及其应用:1.3.2 函数的极值与导数
文档属性
| 名称 | 人教版选修2-2导数及其应用:1.3.2 函数的极值与导数 |
|
|
| 格式 | rar | ||
| 文件大小 | 97.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-26 00:00:00 | ||
图片预览

文档简介
1.3.2 函数的极值与导数(教案)
教学目标
1 知识与技能
〈1〉结合函数图象,了解可导函数在某点取得极值的必要条件和充分条件
〈2〉理解函数极值的概念,会用导数求函数的极大值与极小值
2 过程与方法
结合实例,借助函数图形直观感知,并探索函数的极值与导数的关系。
3 情感与价值
感受导数在研究函数性质中一般性和有效性,通过学习让学生体会极值是函数的局部性质,增强学生数形结合的思维意识。
重点与难点
(1)重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤
(2)难点:函数在某点取得极值的条件
教学基本流程
1、回忆函数的单调性与导数的关系,与已有知识的联系
2、创设情景,激发求知欲
3、组织学生自主探索,获得函数的极值定义,了解可导函数在某点取得极值的条件
4、通过例题和练习,深化提高对函数的极值定义的理解
教学过程
一、复习回顾
1、通过上节课的学习,导数和函数单调性的关系是什么?
学生回答 :在某个区间内,如果,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减.如果,那么函数在这个区间内是常函数.
2.求解函数单调区间的步骤?
生答:(1)确定函数的定义域;
(2)求导数;
(3)解不等式,解集在定义域内的部分为增区间;
(4)解不等式,解集在定义域内的部分为减区间.
二、创设情景,导入新课
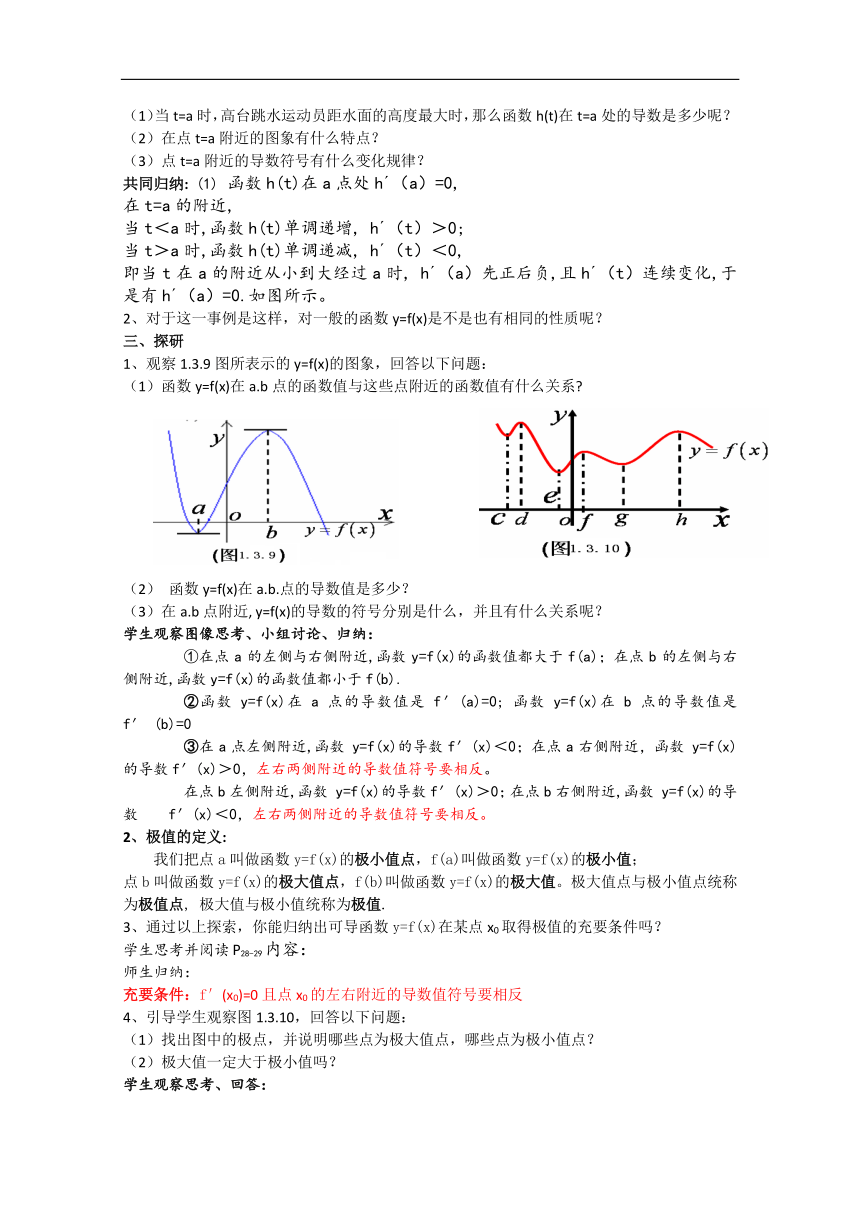
1.观察图1.3.8 表示高台跳水运动员的高度h随时间t变化的函数h(t)=-4.9t +6.5t+10的图象,回答以下问题
图1.3.8
(1)当t=a时,高台跳水运动员距水面的高度最大时,那么函数h(t)在t=a处的导数是多少呢?
(2)在点t=a附近的图象有什么特点?
(3)点t=a附近的导数符号有什么变化规律?
共同归纳: (1) 函数h(t)在a点处h (a)=0,
在t=a的附近,
当t<a时,函数h(t)单调递增, h (t)>0;
当t>a时,函数h(t)单调递减, h (t)<0,
即当t在a的附近从小到大经过a时, h (a)先正后负,且h (t)连续变化,于是有h (a)=0.如图所示。
2、对于这一事例是这样,对一般的函数y=f(x)是不是也有相同的性质呢?
三、探研
1、观察1.3.9图所表示的y=f(x)的图象,回答以下问题:
(1)函数y=f(x)在a.b点的函数值与这些点附近的函数值有什么关系
(2) 函数y=f(x)在a.b.点的导数值是多少?
(3)在a.b点附近, y=f(x)的导数的符号分别是什么,并且有什么关系呢?
学生观察图像思考、小组讨论、归纳:
①在点a的左侧与右侧附近,函数y=f(x)的函数值都大于f(a);在点b的左侧与右侧附近,函数y=f(x)的函数值都小于f(b).
②函数y=f(x)在a点的导数值是f′(a)=0; 函数y=f(x)在b点的导数值是 f′ (b)=0
③在a点左侧附近,函数 y=f(x)的导数f′(x)<0;在点a右侧附近,函数 y=f(x)的导数f′(x)>0,左右两侧附近的导数值符号要相反。
在点b左侧附近,函数 y=f(x)的导数f′(x)>0;在点b右侧附近,函数 y=f(x)的导数 f′(x)<0,左右两侧附近的导数值符号要相反。
2、极值的定义:
我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;
点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值。极大值点与极小值点统称为极值点, 极大值与极小值统称为极值.
3、通过以上探索,你能归纳出可导函数y=f(x)在某点x0取得极值的充要条件吗?
学生思考并阅读P28-29内容:
师生归纳:
充要条件:f′(x0)=0且点x0的左右附近的导数值符号要相反
4、引导学生观察图1.3.10,回答以下问题:
(1)找出图中的极点,并说明哪些点为极大值点,哪些点为极小值点?
(2)极大值一定大于极小值吗?
学生观察思考、回答:
师生归纳:极值反映了函数在某一点附近的大小情况,刻画的是函数的局部性
四.讲解例题、升华理解
例4、求函数f(x)= x -4x+4的极值
1、 师生分析:①求f (x),解方程f (x)=0,找函数极点;
②由函数单调性确定在极点x0附近f/(x)的符号,从而确定哪一点是极大值点,哪一点为极小值点,从而求出函数的极值.
2、学生动手做,教师巡视指导
3、解题规范
解:∵f(x)=x -4x+4∴f (x)=x2-4=(x-2)(x+2)
令f (x)=x2-4=0,解得x=2,或x=-2.
下面分两种情况讨论:
当f (x)>0,即x>2,或x<-2时;
当f (x)<0,即-2<x<2时.
当x变化时, f (x) ,f(x)的变化情况如下表:
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
f (x) + 0 _ 0 +
f(x) 单调递增 ↗ 单调递减 ↘ - 单调递增 ↗
因此,当x=-2时,f(x)有极大值,且极大值为f(-2)=;当x=2时,f(x)有极
小值,且极小值为f(2)=-
函数f(x)= x -4x+4的大致图象如右图所示:
归纳:求函数y=f(x)极值的方法是:
1求f (x);2解方程f (x) =0,当f (x0) =0时:
(1)如果在x0附近的左侧f (x)>0,右侧f (x)<0,那么f(x0)是极大值.
(2)如果在x0附近的左侧f (x)<0,右侧f (x)>0,那么f(x0)是极小值
4、挑战自我:
(1)求函数f(x)=3x-x3的极值
(2)已知函数f(x)=ax3+bx2-2x在x=-2,x=1处取得极值,求函数f(x)的解析式及单调区间。
学生独立完成:
规范解题:(落)
五、课堂小结:
1、函数极值的定义:
2、可导函数y=f(x)在某点x0取得极值的充要条件:
3、求函数y=f(x)的极值的步骤:
六作业
1、 P32 习题1.3 A组 T4、 T5
2、课后思考题:
(1)若函数f(x)=x3-3bx+3b在(0,1)内有极小值,求实数b的范围。
(2)已知f(x)=x3+ax2+(a+b)x+1有极大值和极小值,求实数a的范围。
教学反思:
t
o
PAGE
教学目标
1 知识与技能
〈1〉结合函数图象,了解可导函数在某点取得极值的必要条件和充分条件
〈2〉理解函数极值的概念,会用导数求函数的极大值与极小值
2 过程与方法
结合实例,借助函数图形直观感知,并探索函数的极值与导数的关系。
3 情感与价值
感受导数在研究函数性质中一般性和有效性,通过学习让学生体会极值是函数的局部性质,增强学生数形结合的思维意识。
重点与难点
(1)重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤
(2)难点:函数在某点取得极值的条件
教学基本流程
1、回忆函数的单调性与导数的关系,与已有知识的联系
2、创设情景,激发求知欲
3、组织学生自主探索,获得函数的极值定义,了解可导函数在某点取得极值的条件
4、通过例题和练习,深化提高对函数的极值定义的理解
教学过程
一、复习回顾
1、通过上节课的学习,导数和函数单调性的关系是什么?
学生回答 :在某个区间内,如果,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减.如果,那么函数在这个区间内是常函数.
2.求解函数单调区间的步骤?
生答:(1)确定函数的定义域;
(2)求导数;
(3)解不等式,解集在定义域内的部分为增区间;
(4)解不等式,解集在定义域内的部分为减区间.
二、创设情景,导入新课
1.观察图1.3.8 表示高台跳水运动员的高度h随时间t变化的函数h(t)=-4.9t +6.5t+10的图象,回答以下问题
图1.3.8
(1)当t=a时,高台跳水运动员距水面的高度最大时,那么函数h(t)在t=a处的导数是多少呢?
(2)在点t=a附近的图象有什么特点?
(3)点t=a附近的导数符号有什么变化规律?
共同归纳: (1) 函数h(t)在a点处h (a)=0,
在t=a的附近,
当t<a时,函数h(t)单调递增, h (t)>0;
当t>a时,函数h(t)单调递减, h (t)<0,
即当t在a的附近从小到大经过a时, h (a)先正后负,且h (t)连续变化,于是有h (a)=0.如图所示。
2、对于这一事例是这样,对一般的函数y=f(x)是不是也有相同的性质呢?
三、探研
1、观察1.3.9图所表示的y=f(x)的图象,回答以下问题:
(1)函数y=f(x)在a.b点的函数值与这些点附近的函数值有什么关系
(2) 函数y=f(x)在a.b.点的导数值是多少?
(3)在a.b点附近, y=f(x)的导数的符号分别是什么,并且有什么关系呢?
学生观察图像思考、小组讨论、归纳:
①在点a的左侧与右侧附近,函数y=f(x)的函数值都大于f(a);在点b的左侧与右侧附近,函数y=f(x)的函数值都小于f(b).
②函数y=f(x)在a点的导数值是f′(a)=0; 函数y=f(x)在b点的导数值是 f′ (b)=0
③在a点左侧附近,函数 y=f(x)的导数f′(x)<0;在点a右侧附近,函数 y=f(x)的导数f′(x)>0,左右两侧附近的导数值符号要相反。
在点b左侧附近,函数 y=f(x)的导数f′(x)>0;在点b右侧附近,函数 y=f(x)的导数 f′(x)<0,左右两侧附近的导数值符号要相反。
2、极值的定义:
我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;
点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值。极大值点与极小值点统称为极值点, 极大值与极小值统称为极值.
3、通过以上探索,你能归纳出可导函数y=f(x)在某点x0取得极值的充要条件吗?
学生思考并阅读P28-29内容:
师生归纳:
充要条件:f′(x0)=0且点x0的左右附近的导数值符号要相反
4、引导学生观察图1.3.10,回答以下问题:
(1)找出图中的极点,并说明哪些点为极大值点,哪些点为极小值点?
(2)极大值一定大于极小值吗?
学生观察思考、回答:
师生归纳:极值反映了函数在某一点附近的大小情况,刻画的是函数的局部性
四.讲解例题、升华理解
例4、求函数f(x)= x -4x+4的极值
1、 师生分析:①求f (x),解方程f (x)=0,找函数极点;
②由函数单调性确定在极点x0附近f/(x)的符号,从而确定哪一点是极大值点,哪一点为极小值点,从而求出函数的极值.
2、学生动手做,教师巡视指导
3、解题规范
解:∵f(x)=x -4x+4∴f (x)=x2-4=(x-2)(x+2)
令f (x)=x2-4=0,解得x=2,或x=-2.
下面分两种情况讨论:
当f (x)>0,即x>2,或x<-2时;
当f (x)<0,即-2<x<2时.
当x变化时, f (x) ,f(x)的变化情况如下表:
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
f (x) + 0 _ 0 +
f(x) 单调递增 ↗ 单调递减 ↘ - 单调递增 ↗
因此,当x=-2时,f(x)有极大值,且极大值为f(-2)=;当x=2时,f(x)有极
小值,且极小值为f(2)=-
函数f(x)= x -4x+4的大致图象如右图所示:
归纳:求函数y=f(x)极值的方法是:
1求f (x);2解方程f (x) =0,当f (x0) =0时:
(1)如果在x0附近的左侧f (x)>0,右侧f (x)<0,那么f(x0)是极大值.
(2)如果在x0附近的左侧f (x)<0,右侧f (x)>0,那么f(x0)是极小值
4、挑战自我:
(1)求函数f(x)=3x-x3的极值
(2)已知函数f(x)=ax3+bx2-2x在x=-2,x=1处取得极值,求函数f(x)的解析式及单调区间。
学生独立完成:
规范解题:(落)
五、课堂小结:
1、函数极值的定义:
2、可导函数y=f(x)在某点x0取得极值的充要条件:
3、求函数y=f(x)的极值的步骤:
六作业
1、 P32 习题1.3 A组 T4、 T5
2、课后思考题:
(1)若函数f(x)=x3-3bx+3b在(0,1)内有极小值,求实数b的范围。
(2)已知f(x)=x3+ax2+(a+b)x+1有极大值和极小值,求实数a的范围。
教学反思:
t
o
PAGE
